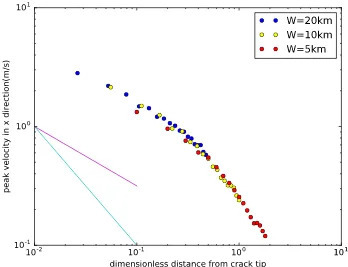
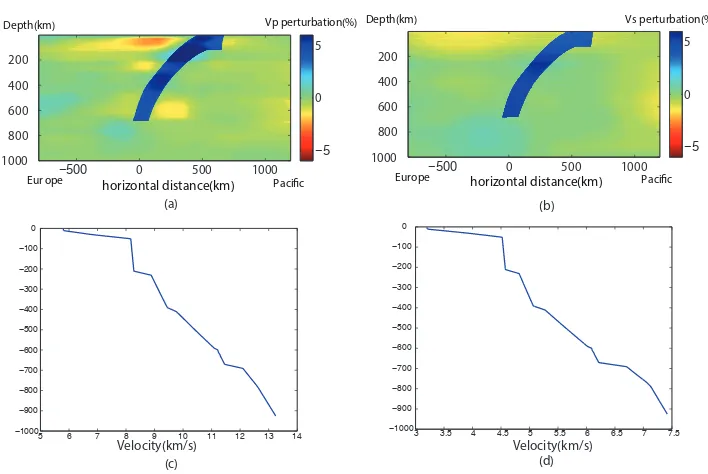
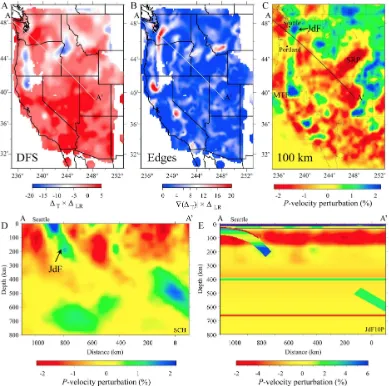
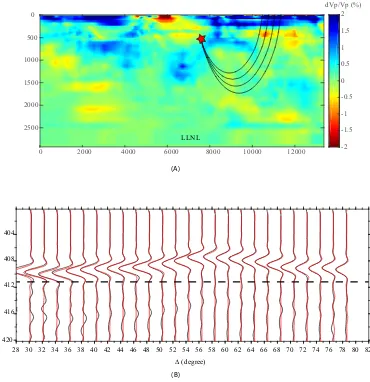
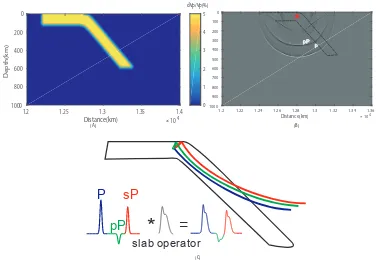
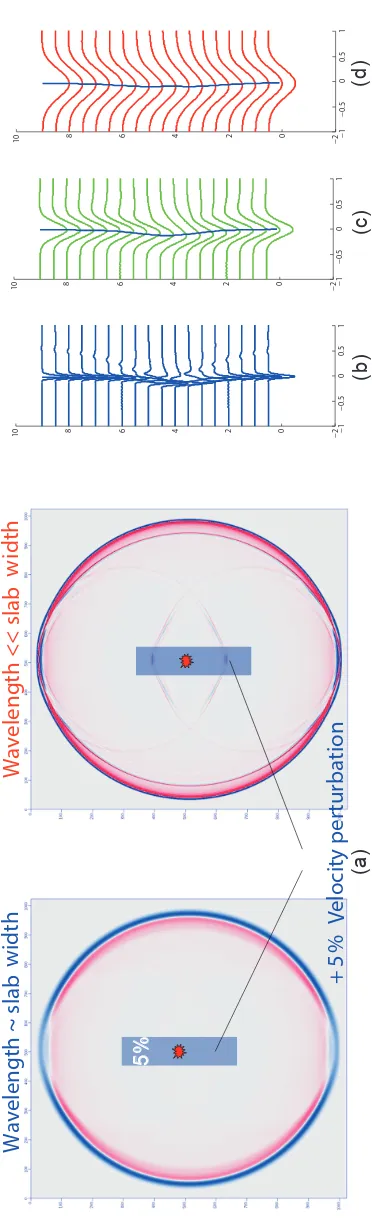
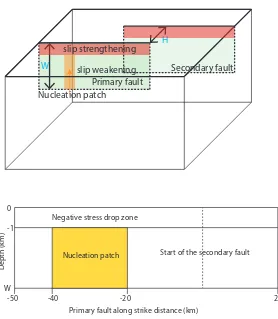
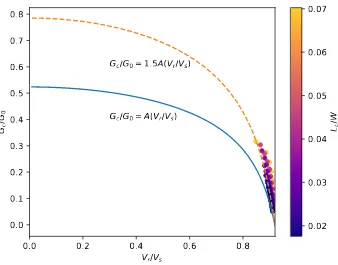
Dynamic Earthquake Source Modeling and the Study of Slab Effects
Full text
Figure
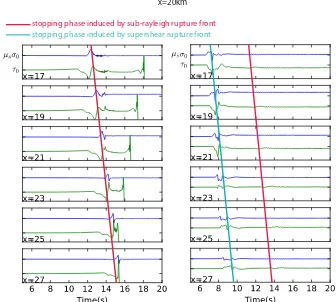
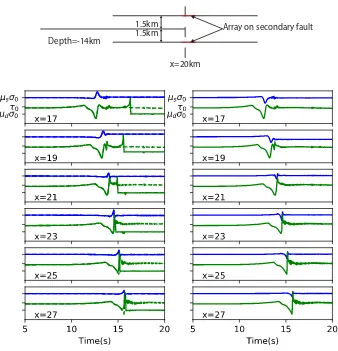
Related documents
Jost: The problem is this: On one hand, IT systems are becoming increasingly flexible—the buzzword being service-oriented architecture—and on the other, IT staff often lack
process more in line with generational charac- teristics, not all of their traits are conducive to learning, (p15). Therefore, educators should feel comfortable helping students
Table 21 shows the ANCOVA results used to determine if any significant differences existed between the posttest scores of coached and noncoached participants in each of the
Because of the shortage of studies undertaken on the relation of innovation and productivity at firm level in Brazil, this study contributes to the empirical debate on the subject
To do so, an access request is sent including, among other, the following context information: user or role requesting access, the operation requested, the time when the request
1) This activity requires students to rewrite the poem paraphrasing it into prose. Students are asked to write a short-story of between two to four hundred words based on the
You will also want to start developing test cases and scripts ensuring that you are testing the entire workflow along with any external systems.. If you just develop the test cases
As such, this study was undertaken to investigate the relationship between employee satisfaction and quality service from the aspects of tangible, reliability and