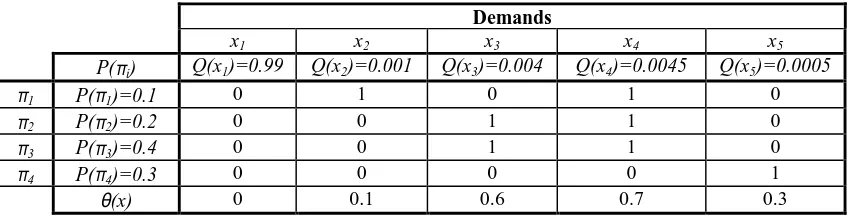
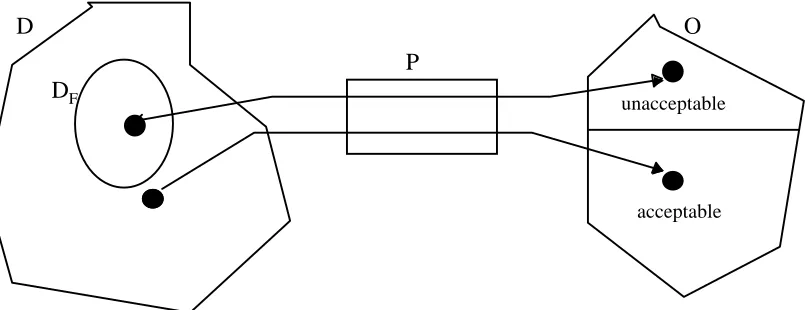
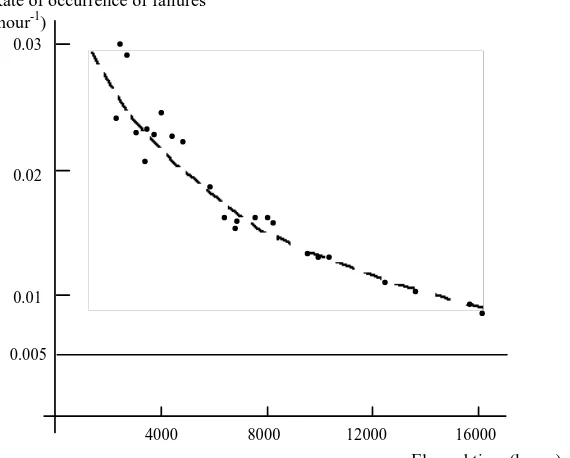
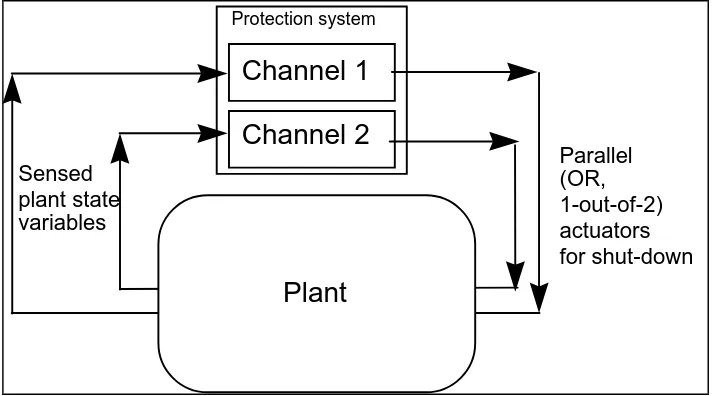
Modeling software design diversity
Full text
Figure

Related documents
The Climate Change, Agriculture and Food Security Research Program (CCAFS) of the Consultative Group for International Agricultural Resources (CGIAR) CCAFS “seeks to overcome
Studies reporting the prevalence of burnout, com- passion fatigue, secondary traumatic stress and vicarious trauma in ICU healthcare profes- sionals were included, as well as
Computer software engineers apply the principles of computer science and mathematical analysis to the design, development, testing, and evaluation of the software and systems
Port d’Alon guided underwater trail (France) : The Conservatoire du Littoral, the site owner, and the town council that manages the site have delegated the entire
Students wishing to pursue the two-year degree or the certificate programs must be signed into courses by the program director at the beginning of each semester to ensure that they
Range of Sprocket Teeth Available With Type A Tooth Form Sprockets ... Standard Pitch Diameter, Maximum Outside andBottom Diameter, and Pressure.. Angle Limits
decide on money instead of contracts see, for instance, Shapley and Shubik, 1972, Roth and Sotomayor, 1990, and Pérez-Castrillo and Sotomayor, 2002). Any stable outcome is also
In 2005, Dell‟s main objective on online strategy was to improve the quality perception of their products by optimising processes as well as harmonizing the creative expression in