Hardness-strength relationships in the aluminum alloy 7010
Full text
Figure


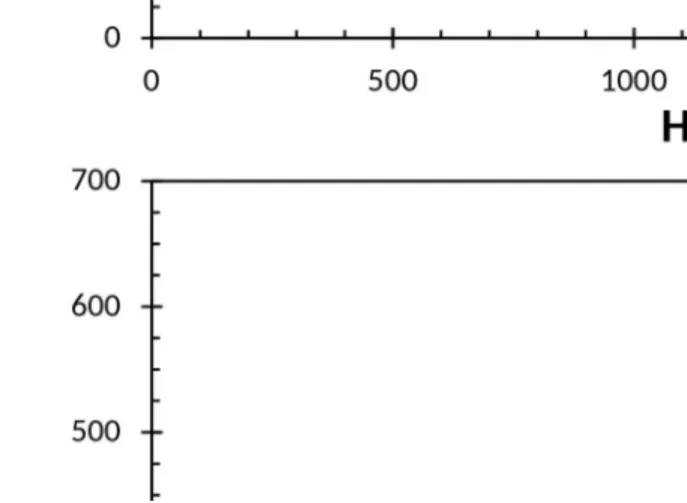
![Figure 3.Vickers hardness versus yield stress relationship drawn from the data of Flynn [39,40]](https://thumb-us.123doks.com/thumbv2/123dok_us/8047955.222704/14.918.114.801.116.617/figure-vickers-hardness-versus-yield-stress-relationship-flynn.webp)
Related documents
2 Underlying operating profit is operating profit of subsidiaries and joint ventures before special items. 3 Underlying profit before tax is reported profit before tax before
The African Union Commission embarked on a consultative mission to Juba from 20 to 22 July 2017, to engage the Transitional Government of National Unity on implementating Chapter 5
We note that for Hall measurements, we have grown thick samples (1150 nm) on a SOI substrate (Silicon On Insulator) to avoid any transport contribution coming from
Table I provides information concerning fiscal year 2010 capital expenditures and related information for those Illinois health care facilities that reported data.. Total
Meeting the welfare needs of dogs is often closely linked to ‘responsible dog ownership’. In the UK, this concept has been promoted by the Kennel Club [ 40 ], the British
By comparing the south-east with the north-east panels we see that under this tax scheme the sign of the marginal e¤ect of capital taxation is exactly the opposite to the one found
Unlike rainfall threshold-based methods that uses the historical/synthesized rainfall events, the real-time simulation method can be an alternative by directly incorporating nowcast
The general goals of this research are: 1) to study the shear behavior of prestressed concrete I-beams strengthened with CFRP; 2) to quantify the added shear capacity of the CFRP; 3)