G. Pelegr´ı,1 J. Mompart,1 V. Ahufinger,1 and A. J. Daley2 1
Departament de F´ısica, Universitat Aut`onoma de Barcelona, E-08193 Bellaterra, Spain. 2Department of Physics and SUPA, University of Strathclyde, Glasgow G4 0NG, United Kingdom.
We show how strongly correlated ultracold bosonic atoms loaded in specific orbital angular mo-mentum states of arrays of cylindrically symmetric potentials can realize a variety of spin-1/2 models of quantum magnetism. We consider explicitly the dependence of the effective couplings on the ge-ometry of the system and demonstrate that several models of interest related to a general XY Z Heisenberg model with external field can be obtained. Furthermore, we discuss how the relative strength of the effective couplings can be tuned and which phases can be explored by doing so in realistic setups. Finally, we address questions concerning the experimental read-out and implemen-tation and we argue that the stability of the system can be enhanced by using ring-shaped trapping potentials.
I. INTRODUCTION
Ultracold atoms in optical lattices provide a clean and highly tunable playground to study a plethora of many-body phenomena [1]. Recent years have witnessed impor-tant breakthroughs that have pushed the degree of con-trol over these systems to a very precise quantitative level and have opened new routes towards the quantum simu-lation of previously unexplored systems in a wide range of fields [2]. In particular, ultracold atoms have proven to be a very powerful tool for exploring quantum magnetism in a form originally inspired by solid state systems. Re-markable achievements of quantum simulation of mag-netism with ultracold atoms include the implementation of spin-frustrated lattices [3, 4], extensive experimental studies of the magnetic properties of the Hubbard model [5–12], or the realization of high-resolution quantum gas microscopes for bosonic atoms [13, 14] that have lead to the observation of anti-ferromagnetic order in a one-dimensional (1D) Ising chain [15], bound magnons in the
XXZ Heisenberg model [16] and spin-resolved dynamics [17–19]. There are also proposals to realize spin mod-els with strongly interacting ultracold bosons excited to
p−bands [21], and realizations of magnetic models with bosons in tilted optical lattices [15,22–25].
In this paper, we show that strongly interacting ul-tracold bosons loaded into Orbital Angular Momentum (OAM) states of lattices of side-coupled cylindrically symmetric traps can realize a variety of spin-1/2 mod-els, including theXY Z Heisenberg model with or with-out external field. In particular, we focus on the Mott insulator regime at unit filling, where each trap is occu-pied by a single atom and a direct mapping between the OAM and spin-1/2 states can be performed. Recently, a proposal to realize such a state by periodically modulat-ing an optical lattice has been made [26]. Alternatively, this state could be generated by optically transferring OAM [27] to atoms confined to an arrangement of ring-shaped potentials, which can be created by a variety of techniques [28–38] and have proven to support long-lived persistent currents associated to the OAM states [39,40]. The mechanisms that yield these effective spin-1/2
mod-els are analogous to the ones described in [21], where it was shown that the XY Z Heisenberg model can be realized with ultracold bosons in thep-bands of a two-dimensional optical lattice [41,42], which are equivalent to the OAMl= 1 states. Our proposal, however, extends this to lattices made up of general cylindrically symmet-ric potentials such as ring traps, and is valid for higher OAM states. The new degree of control offered by the flexibility in the arrangements of the traps opens up the possibility to engineer a wide variety of spin models be-yond theXY Z Heisenberg model and makes it possible to modify the effective coupling parameters at the level of a single site.
The rest of the paper is organized as follows. In sec-tionII, we describe the general physical system and give details of how to compute the couplings that govern the effective spin-1/2 model. In section III, we make con-crete proposals to implement different spin-1/2 models of interest by arranging the ring potentials in different geometries. In section IV, we discuss how the effective couplings can be tuned experimentally and which phases of theXY Z model can be explored by doing so. In sec-tionV, we discuss the implementation of lattices of ring potentials and the readout and stability of OAM states in an experimental realization. Finally, in sectionVIwe summarize the main conclusions of this work.
II. QUASI ONE-DIMENSIONAL LADDER AND EFFECTIVE SPIN-1/2MODEL
For the sake of clarity, we start by considering in this section the simplest quasi one-dimensional lattice in which an effective spin-1/2 model of quantum mag-netism can be obtained using ultracold atoms carrying OAM, namely an array of equivalent ring-shaped poten-tials. From the analysis of the second order processes that we will discuss for this system, the generalization of the effective spin model to other quasi one-dimensional geometries and to two-dimensional lattices is straightfor-ward.
The quasi one-dimensional system on which we focus consists of a gas ofMultracold bosons of massmtrapped
Figure 1. Quasi one-dimensional ladder of ring potentials (labelled by the indexj) obtained by concatenating unit cells (labelled by the indexi) formed by two rings such that the central angle of the triangles formed by three neighbouring rings is Θ. The origin of phases is taken along the direction 2i ↔ 2i+ 1 (indicated with blue straight arrows), so that the couplings are real along this direction and all hopping phases appear in the 2i↔ 2i−1 links (indicated with red dashed arrows). The distance between the closest points of two nearest-neighbour rings isd.
in a ladder ofN identical ring-shaped potentials, labelled by the indexj. This can be constructed by concatenat-ing N/2 two-ring unit cells, labelled by the index i, as depicted in Fig. 1. All of the rings have the same ra-dius R and radial trapping frequency ω, which defines the natural length scaleσ=p~/mω. The outer parts of
two rings belonging to the same unit cell are separated a distanced, and three consecutive rings form a triangle with a central angle Θ. The bosons may occupy the two degenerate eigenstates of total OAM l ≥1 of each ring,
|j,±li, for which the wavefunctions are given by
φj±l(rj, ϕj) =h~r|j,±li=ψl(rj)e±il(ϕj−ϕ0), (1)
where (rj, ϕj) are the polar coordinates with origin at the center of the jth ring and ϕ0 is an arbitrary origin of phases. The radial part of the wavefunction, ψl(rj), can be approximated by the ground state of thejth ring potential,ψ0(rj). Under this approximation, the energy of the modes of OAMl is given by
E(l) =E0+Ecl2, (2)
where E0 is the energy of the ground state of the ring
andEc = ~
2
2m R
d2r
ψ0(r)
r 2
is the centrifugal part of the
kinetic energy. We assume that the motion of the bosons is restricted to the manifold of states of total OAMl, i.e., values of±l, without coupling to other OAM manifolds. In this situation, the total bosonic field operator of the system reads
ˆ Ψl=
N X
j=1
φj+l(rj, ϕj)ˆaj+l+φj−l(rj, ϕj)ˆaj−l (3)
where ˆa±lare the bosonic annihilation operators associ-ated with the respective OAM modes. The Hamiltonian of the system can be decomposed into its single particle
and interacting parts
ˆ
Hl= Z
d~rΨˆ†l
−~
2∇2
2m +V(~r)
ˆ Ψl+g
2 Z
d~rΨˆ†lΨˆ†lΨlˆ Ψlˆ
≡Hˆ0 l + ˆH
int
l , (4)
whereV(~r) is the total trapping potential of the ladder, which can be approximated by a truncated combination of all the ring potentials Vj(r) = 12mω2(R−rj)2, and
gis the strength of thes−wave atom-atom interactions. The kinetic part of the Hamiltonian, ˆHl0, describes the tunneling dynamics of the states of total OAMlbetween neighbouring rings as well as between the two degener-ate stdegener-ates within the same ring. This type of dynamics was studied in detail in [43]. By analysing the mirror symmetries of the two-ring problem, it can be shown that there are only three independent coupling ampli-tudes which correspond, respectively, to the tunneling within a ring, Jl
1 = hj,±l|Hˆ|j,∓i, the tunneling to a neighbouring ring without exchange of the OAM circu-lation,J2l =hj,±l|Hˆ|j+ 1,±li, and the tunneling to a neighbouring ring with exchange of the OAM circulation,
Jl
3=hj,±l|Hˆ|j+ 1,∓li. Assuming that the central angle takes values Θ> π/3, one can consider that only nearest-neighbour sites are coupled. By making this approxima-tion and choosing the origin of phases to be along the line that unites the sites 2i↔2i+ 1, so thatϕ0=π−Θ along the 2i−1↔2idirection, the single particle terms of the Hamiltonian take the form
ˆ
Hl0=J l 1
N X
j=1 ˆ
aj+l†ˆaj−l(1 +e−i2lΘ)
+J2l
N/2 X
i=1 ˆ
a+l2i†(ˆa2i+1+l + ˆa2i+l−1) + ˆa−2il†(ˆa2i+1−l + ˆa2i−l−1)
+J3l
N/2 X
i=1 ˆ
a2i+l†(ˆa2i+1−l +e−i2lΘˆa2i−l−1)
+J3l
N/2 X
i=1 ˆ
a2i−l†(ˆa2i+1+l +ei2lΘaˆ2i+l−1) + h.c. (5)
Assuming that only on-site interactions take place, the interacting part of the Hamiltonian can be written as
ˆ
Hlint=U 2
N X
j=1 ˆ
nj+l(ˆnj+l−1)+ ˆnj−l(ˆnj−l−1)+4ˆnj+lˆnj−l, (6)
withU =gR
d~r|ψ0(r)|4.
We now focus on the scenario in which the ladder is at unit filling, M = N, and the interaction strength is positive and much larger than the tunneling energies,
U |Jl
or negative OAM circulation of the boson. We can per-form a direct mapping between these states and a spin-1/2 configuration by identifying a spin up (down) for each ring with a boson in the state of positive (negative) OAM circulation, i.e., |j,+li → |↑ij;|j,−li → |↓ij.
Further-more, we can define the spin-flip operatorsσ±j =aj±†laj∓, which can be expressed in terms of the x and y Pauli matrices asσj±= 12(σx
j±iσ y
j). We also define thezPauli matrix as σz
j = a j†
+la j +l−a
j† −la
j
−l and the spin up and down projectorsPj↑=aj+l†aj+l,Pj↓=aj−†laj−l.
The physics of the ladder in the Mott Insulator phase can be described by an effective model that incorpo-rates interaction terms between the neighbouring spins induced by the kinetic part of the Hamiltonian, ˆH0
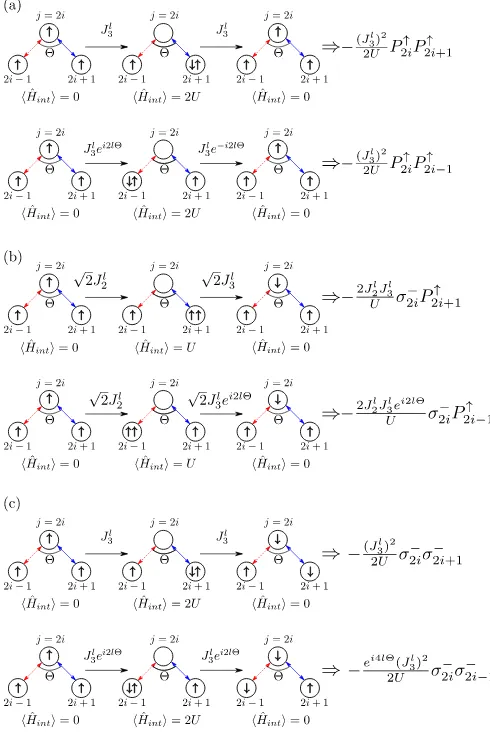
l, which we treat as a perturbation. This follows the same form as the usual reduction of Hubbard, Bose-Hubbard and related models in the Mott Insulator regime to spin models. More details on the derivation of the effective model can be found in Appendix A. The new element here comes from the tunnelling phase, which can lead to non-trivial dependence of the effective model on the ge-ometry of the lattice. The resulting effective Hamiltonian contains four types of processes. As sketched in Fig. 2, there are three different kinds of second order processes induced by the effective interaction: those in which the final states of the ringsj andj±1 have 0, 1, or 2 spins flipped with respect to the initial state. Furthermore, there is a first order process which corresponds to the flipping of a single spin due to the self-coupling. Next, we compute separately the amplitudes corresponding to each of these different processes.
Processes involving no spin flips
The first type of second order processes that we con-sider are those in which the initial and final states coin-cide, i.e., no spins are flipped. In Fig. 2(a) we show two examples of such processes, one in which a boson at ring
[image:3.612.315.560.53.420.2]j = 2i tunnels to j = 2i+ 1 and back and another one in which it tunnels to j = 2i−1. In spite of the fact that along the direction 2i ↔ 2i−1 there are hopping phases in the tunneling terms that exchange angular mo-mentum, in the total second order processes they cancel out because there have to be two opposite flips in order to come back to the initial state. Thus, the total am-plitude of these processes is the same regardless of the direction of the interaction. For each pair of interacting rings, there are in total 16 different second order pro-cesses not involving any total spin flip, which correspond to the 4 possible two-ring spin configurations and the 4 possible doubly occupied virtual states that mediate the interaction. Adding up all the amplitudes of these processes and using the spin notation, we find that the part of the effective Hamiltonian corresponding to these
Figure 2. Sketch of some of the second order processes that take place in the Mott insulator regime and their associated amplitudes. (a) Second order processes not involving any flip-ping of the spins. (b) Second order processes leading to the flipping of one spin at site 2i. (c) Second order processes lead-ing to the simultaneous flipplead-ing of the spins at sites 2iand 2i+ 1 (upper figure) and at sites 2iand 2i−1 (lower figure).
processes reads
ˆ
Hj0flip↔j±1=−3((J
l
2)2−(J3l)2)
2U σ
z jσ
z j±1−
5((Jl
2)2+ (J3l)2)
2U I
(7) We note that these amplitudes do not depend on the position of the ringjinside the unit cell where it belongs.
Processes involving one spin flip
The first possibility to flip a single spin in the ring j
is by the action of the self-couplingJ1l. The total ampli-tude for this process is (1 +ei2lΘ)σ−j + (1 +ei2lΘ)σj+ =
Jl
1(σxj(1 + cos 2lΘ) +σ y
j sin 2lΘ).
exam-ples of second order processes that lead to the flipping of a spin at the ringj = 2i, one with a virtual interac-tion occurring at j = 2i+ 1 and another one mediated by the ring j = 2i−1. In this case, the amplitudes of the processes depend on the direction of the interaction: when they occur along j = 2i ↔ 2i+ 1 they are real, whereas along the line j = 2i ↔ 2i−1 a net hopping phase appears. Adding up all the amplitudes of the 12 different second order processes that lead to the flipping of a single spin, we find
ˆ
Hj1flip=
J1l−3J
l 2J3l
U
(σjx(1 + cos 2lΘ) +σyjsin 2lΘ)
(8) Again, the total amplitude does not depend on the po-sition of j inside the unit cell because all rings are cou-pled to a ring along each of the two directions with dif-ferent hopping phases. For values of the central angle such thatlΘ =π/2 (mod2π), the single spin-flip ampli-tude vanishes, and for lΘ = 0, π (mod2π), it becomes
ˆ
Hj1flip=2J1l−6J2lJ3l
U
σjx.
Processes involving two spin flips
Finally, in Fig. 2 (c) we show two examples of second order processes that lead to the simultaneous flipping of two spins. As in the case of single spin-flip processes, along the j = 2i ↔ 2i−1 interaction direction there are no total cancellations of the hopping phases. Thus, the sum of the amplitudes of these processes depends on the direction along which the bosons interact. Adding up the 8 possible processes that lead to the simultaneous flipping of two spins in the final states, we find
ˆ
H2i2flip↔2i+1=−(J
l
2)2+ (J3l)2
2U σ
x 2iσ
x 2i+1−
(Jl
2)2−(J3l)2
2U σ
y 2iσ y 2i+1 (9) ˆ
H2i2flip↔2i−1=−(J
l 2)
2+ cos 4lΘ(Jl 3)
2
2U σ
x 2iσ
x 2i−1
−(J
l 2)
2−cos 4lΘ(Jl 3)
2
2U σ
y 2iσ
y 2i−1
−cos 4lΘ(J
l 3)
2
2U (σ
x 2iσ
y 2i−1+σ
y 2iσ
x
2i−1) (10)
For central angles such thatlΘ =π/2, π/4 (mod2π), the two-spin flip processes have equal amplitude along the two directions.
III. XYZ MODELS
By tuning the central angle Θ, the amplitudes of the second order processes can be modified in order to engi-neer a range of quantum magnetic models. Next, we give examples of specific geometric arrangements of the ring potential ladder that lead to interesting effective spin-1/2 models.
A. XYZ model without external field
For central angles Θls= (2s+ 1)π/2l, withs∈N, the single-spin flip term vanishes and the two-spin flip term becomes isotropic. Summing over all the sites and pro-cesses and neglecting the constant term that appears in the zero-spin flip terms, we arrive at the following effec-tive Hamiltonian of the Mott insulator regime
ˆ
Heffl (Θls) = N X
j=1
Jxxl σjxσj+1x +Jyyl σjyσj+1y +Jzzl σjzσzj+1,
(11) where Jl
xx = −((J2l)2 + (J3l)2)/2U, Jyyl = −((J2l)2 − (Jl
3)2)/2U andJzzl =−3((J2l)2−(J3l)2)/2U. The Hamil-tonian (11) is equivalent to the one of the Heisenberg
XY Z model, which is a prominent model of quantum magnetism and is exactly solvable [44].
B. XYZ model with external field
For values of the central angle ¯Θl
s = 2Θls, the single-spin flip amplitude contains onlyσxone-body terms and the two-spin flip term remains isotropic. Thus, for these particular values of Θ the effective model of the ladder becomes
ˆ
Heffl (Θls) = N X
j=1
Jxxl σxjσj+1x +Jyyl σ y jσ
y j+1+J
l
zzσjzσj+1z
+hl
N X
j=1
σxj, (12)
with hl = 2Jl
1−6J2lJ3l/U. The Hamiltonian (12) cor-responds to aXY Z Heisenberg model with an external fieldhlalong thexdirection. In the system ofp−orbital bosons described in [21], the external magnetic field is created by the imbalance between thepx and py inter-action strengths and on-site energies, while in the ladder of rings loaded with OAM states that we consider here it arises as a consequence of the geometry of the system.
C. XYZ model with staggered fields
Figure 3. Ladder of ring potentials with four sites per unit cell. The origin of phases is taken along the directionAi ↔
Bi ↔ Ci (indicated with blue straight arrows), so that the
couplings are taken real along this direction and all hopping phases appear in theCi↔Di ↔Ai+1 links (indicated with
red dashed arrows). The distance between the closest points of two nearest-neighbour rings isd.
phases along the line Ai ↔Bi ↔ Ci, the effective spin Hamiltonian of this system reads
Heffl=1(Θ =π/2) =X j
Jxx1 σxjσj+1x +Jyy1 σjyσyj+1+Jzz1 σjzσj+1z
+h1X
i
σBxi−σxDi. (13)
In the model (13), the external magnetic fields appear in a staggered pattern only at theBi andDi sites.
IV. CONTROL OVER PARAMETERS AND QUANTUM PHASES THROUGH THE TRAP
GEOMETRY
In this section, we describe how the effective parame-ters of the spin−1/2 models can be tuned by modifying the size of the ring potentials and the separation between them. We also discuss the different phases of the XY Z
model without external field (11) that can be explored with the system and we analyze their robustness against deviations of the central angle of the ladder from the val-ues Θlsthat yield the effective model (11). Although we focus on the case of l = 1 OAM states, our considera-tions can be generalized to other OAM manifolds in a straightforward manner.
A. Control of the effective model parameters
In a two-ring system, it is possible to compute the values of the tunneling parameters{J11, J21, J31}by calcu-lating numerically the energies of the OAM eigenstates of the system, which are related to the hopping strengths via a four-state model [43]. This procedure determines the dependence of the relative values of the couplings on the ring radiusRand the separation between rings d
[47]. For small values of the inter-ring distance d ∼σ,
J1
3 is several times larger than J21. As shown in Fig. 4
Figure 4. Dependence of the effective couplings of theXY Z model (11) on the inter-ring separationdfor rings ofR= 2.5σ (a) and rings ofR= 5.0σ(b). The dashed vertical lines mark the value of d for which the transition of the XY Z model without external field (11) between thez-antiferromagnet and thex-ferromagnet occurs. (c) Dependence of the ratioJ1
1/J31
on the inter-ring separation. The inset shows the dependence ofh1 on the inter-ring separation taking U/J31 = 20 for all
values ofd.
[image:5.612.319.562.60.516.2]range of inter-ring separations for which the condition 3Jyy =Jzz>−Jxx holds.
In this parameter regime, theXY Zmodel without ex-ternal field (11) is in a anti-ferromagnetic phase in thez
direction [48]. Asdis increased,J1
3 andJ21become more similar, until the critical point Jzz = −Jxx is reached. This point, which is signalled with dashed vertical lines in Fig. 4(a), (b), marks the transition to a ferromagnetic phase in thexdirection [48]. In the limit of very larged,
J1
3 =J21 and thereforeJzz=Jyy = 0. The behaviour of the ratioJ1
1/J31 as a function ofdis shown in Fig. 4 (c) for rings of R = 2.5σ and R = 5σ. For small values of d, J11 has the same sign as J31 and is of the same order or higher. Asd is increased,J1
1/J31 decreases until zero, and then it remains small and neg-ative. As shown in the inset of Fig. 4(c), this behaviour of the J1
1/J31 ratio translates into the effective field h1 being positive at small values ofd, and asdis increased decreasing to a minimum negative value and finally re-maining negative and with an approximately constant value.
B. Example properties of the obtainable quantum phases
In order to analyse numerically the phases of ladders with different central angles Θ, we have performed exact diagonalization in chains of up toN = 16 spins with Pe-riodic Boundary Conditions (PBC). If a quantum critical point exists, we expect that the energy gap ∆ between the ground and first excited state scales with the system size as ∆∼ 1
N [22]. Therefore, we have searched for the critical point by plotting for ladders of different sizes the quantity ∆N as a function of the inter-ring separation
dand looking at the point where all the lines intersect. In order to confirm directly the presence of the tran-sition point between the z−antiferromagnetic and the
x−ferromagnetic phases, we have also computed for a ladder of N = 16 spins with PBC the ground state cor-relations between two fixed spins as a function ofd.
In Fig. 5 (a) we show the results of these two anal-yses for a ladder formed by rings of R = 2.5σ, filled with bosons in l = 1 OAM states and with a central angle Θ = π2, which is described by the XY Z model without external field (11). The upper plots shows the dependence of ∆N on d for different system sizes. As expected, all the lines intersect at the value of d for which |Jzz| =|Jxx|, where the phase transition occurs. As shown in the lower plot, in the z−antiferromagnetic phase, the zz correlation is higher than thexxone. As
dincreases, thezzcorrelation decays and thexxone in-creases, until they reach the same value at an inter-ring distance that coincides with the corresponding one for the critical point.
[image:6.612.335.544.64.598.2]In Fig. 5 (b), we perform the same analysis for a lad-der as in Fig. 5 (a) but with a central angle Θ = 0.48π. In the upper plot, we observe that there are two points
Figure 5. Upper plots in (a) and (b): dependence of the energy difference between the ground and first excited states on the inter-ring distancedfor ladders of different sizes formed by rings of radius R = 2.5σ. Lower plots in (a) and (b): correlations between spin 1 and 9 in a ladder ofN= 16 spins with PBC formed by rings ofR = 2.5σ. In (a) the central angle of the ladder is Θ =π
2 and in (b) Θ = 0.48π.
smaller value of d corresponds to a point where thezz
and xx correlations become equal. Therefore, it marks the transition between thez−antiferromagnetic and the
x−ferromagnetic phases. This transition occurs at a smaller value ofdthan in the ladder with a central angle Θ = π2 because of the presence of the magnetic field along thexdirection. For values of the central angle more devi-ated from π2, the presence of the magnetic field destroys the z−antiferromagnetic phase and the transition does not occur. The other point where the ∆N curves inter-sect occurs at a longer value ofdwhich coincides with the point where the external magnetic field vanishes (see the inset of Fig.4(b)). Therefore, it corresponds to a global change of orientation of the spins in thex−ferromagnetic phase.
V. CONSIDERATIONS FOR EXPERIMENTAL IMPLEMENTATIONS
A. Realization of the ring lattices
The arrays of ring traps considered in the previous sec-tions could be created by means of several different tech-niques. Since they were first proposed a few years ago [31, 36], time-averaged adiabatic potentials have proven to be a powerful tool to trap ultracold atoms in on-demand potential landscapes [32,37,38]. Recently, it has also been shown that digital micro-mirror devices allow to create trapping potentials with arbitrary shapes [45], and in particular a double ring trap has been realized [35]. Both of these already demonstrated approaches could be adapted to create lattices of ring potentials. Conical re-fraction, which is a phenomenon that occurs when a fo-cused light beam passes along an optic axis of a biaxial crystal, has also been used to trap ultracold atoms in ring geometries [34]. With this technique, arrays of ring potentials could be generated by reproducing with mi-crolenses the intensity pattern of a laser beam traversing a single crystal. Alternatively, the combination of split lenses and spatial light modulators [46] could also be used to implement arrays of light rings with any desired ge-ometry.
B. Experimental readout of the spin states
Making use of a scheme of two-photon stimulated Ra-man transitions in the Lamb-Dicke regime analogous to the one discussed in [21], the OAM states of a single site could be addressed separately. By tuning the frequencies of the lasers, side-band transitions between the ground state of the ring potential and the±l OAM states could be induced. Once the OAM states are encoded in the in-ternal atomic states, a quantum gas microscope [13, 14] could be used to read the spin states of the effective mod-els with single-site resolution.
In order to select a specific OAM mode, two different approaches could be followed. As pointed out in [21], one option would be to choose the laser beams such that their wave vector difference is oriented along thexor y
direction. In that manner, the lasers would only inter-act with states that have nodes along the x or y axes, which can be expressed as symmetric or anti-symmetric superpositions of OAM modes. Alternatively, with the aid of e.g. spatial light modulators, one could also make a small adiabatic deformation of the ring trap in order to break cylindrical symmetry and induce an energy split-ting between the dressed OAM states such that they can be independently resolved.
C. Collisional stability of the OAM states
An important question concerning the feasibility of the experimental realization of the system is whether col-lisional processes may cause transitions between states with different OAM that invalidate the assumption that all the atoms remain always in the same OAM manifold [49]. These collisional processes are described in the Born approximation by the operator
ˆ
U =g 2
Z
d~rΨˆ†Ψˆ†Ψ ˆˆΨ, (14)
where ˆΨ = P∞
l=0Ψlˆ is the full bosonic field operator of the lattice, given by the sum of all the field operators of the different OAM manifolds (3). In order to analyse the stability of the OAM states under the most relevant col-lisional processes, it is enough to restrict ourselves to the examination of two-boson states in a single ring. This is because the collisional interactions are strongly dom-inated by on-site processes. In the strongly interacting regime, the role of tunnelling is significantly reduced. In the opposite limit where atoms are delocalised, we would have to consider the full Bloch Band widths for energy conservation in a collisional process taking atoms to other OAM states.
place by the population distribution of the many-body states in the ground state [50].
VI. CONCLUSIONS
We have shown that ultracold bosons carrying OAM in arrays of cylindrically symmetric potentials realize a variety of spin−1/2 models of quantum magnetism in the Mott insulator regime at unit filling. By means of second-order perturbation theory, we have computed explicitly the dependence of the effective couplings on the relative angle between the traps and demonstrated that several models of interest such as theXY Z model with uniform or staggered external fields can be obtained. We have discussed how the relative strength of the effective cou-pling parameters can be tuned and which phases of the
XY Z model without external field can be observed in a realistic set-up by performing this tuning. Furthermore, we have analysed the effect of small changes of the rela-tive angles between the traps on these phases. We have also discussed single-site addressing techniques that allow to retrieve the state of each individual spin. Finally, we have analysed the collisional stability of the system and concluded that the anharmonic energy spacing between OAM states introduced by the ring geometry extends the lifetime of the Mott state. Therefore, the scheme presented in this work serves as a versatile toolbox for the quantum simulation of magnetic models and has a feasible experimental implementation.
ACKNOWLEDGMENTS
G.P., J.M., and V.A. gratefully acknowledge financial support from the Ministerio de Econom´ıa y Competi-tividad, MINECO, (FIS2014-57460-P, FIS2017-86530-P) and from the Generalitat de Catalunya (SGR2017-1646). G.P. acknowledges financial support from MINECO through Grant No. BES-2015-073772. Work at the Uni-versity of Strathclyde was supported by the EPSRC Pro-gramme Grant DesOEQ (EP/P009565/1). We thank Anton Buyskikh and Luca Tagliacozzo for helpful dis-cussions.
Appendix A: Derivation of the effective Hamiltonian
To derive the effective Hamiltonian, we define a pro-jector ˆM to the Mott space of singly occupied sites as well as the projector to the space orthogonal to this one
ˆ
O= 1−Mˆ. In terms of these operators, the Schr¨odinger equation ( ˆH0
l + ˆHlint)|Ψi=E|Ψican be decomposed as [21]
( ˆOHˆl0Oˆ+ ˆOHˆl0Mˆ + ˆOHˆlintOˆ+ ˆOHˆlintMˆ)|Ψi=EOˆ|Ψi
(A1)
( ˆMHˆl0Oˆ+ ˆMHˆl0Mˆ + ˆMHˆlintOˆ+ ˆMHˆlintMˆ)|Ψi=EMˆ |Ψi.
(A2)
The terms ˆMHˆlintMˆ, ˆOHˆlintMˆ and ˆMHˆlintOˆare all iden-tically zero: the first two ones for computing two-body interactions in single-ocupied rings and the last one for computing overlaps between orthogonal spaces. Taking this fact into account, we can combine eqs. (A1) and (A2) to write
ˆ
HeffMˆ |Ψi=EMˆ |Ψi, (A3)
where the effective Hamiltonian reads
ˆ
Heff =−MˆHˆl0Oˆ 1 ˆ
OHˆint l Oˆ−E
ˆ
OHˆl0Mˆ + ˆMHˆ0
lM .ˆ (A4)
The physical action of the first term of the effective Hamiltonian is to connect a Mott state to a state of the orthogonal space through the tunneling term of the orig-inal Hamiltonian, associate an energy to this state in the orthogonal space according to ( ˆOHˆint
l Oˆ−E)−1and then take the state back to the Mott subspace. All the second order processes induced by this term occur via intermedi-ate stintermedi-ates in which all the rings are singly occupied except for one ring, sayj, that is empty, and the ringj±1, that is doubly occupied. Therefore, we restrict the orthogonal subspace to the these states, which can be compactly rep-resented by the three possible two-spin states for the dou-bly occupied rings, namely {|↑↑ij±1,|↓↓ij±1,|↑↓ij±1}. Furthermore, since we are in the Mott insulator regime, we can assume that ( ˆOHˆlintOˆ−E)−1≈( ˆOHˆlintOˆ)−1. In the subspace of states where only a single ring has double occupation, this operator takes the form ( ˆOHˆint
l Oˆ)
−1 =
diag{1/U,1/U,1/2U}. The second term of the effective Hamiltonian, ˆMHˆ0
lMˆ, takes into account the first order processes that occur within the subspace of singly occu-pied states, which are due to the self-coupling amplitude
Jl 1.
[1] M. Lewenstein, A. Sanpera, and V. Ahufinger, Ultra-cold Atoms in Optical Lattices (Oxford University Press, 2012).
[2] C. Gross and I. Bloch,Science 357, 995 (2017).
[4] J. Struck, M. Weinberg, C. ¨Olschl¨ager, P. Windpassinger, J. Simonet, K. Sengstock, R. H¨oppner, P. Hauke, A. Eckardt, M. Lewenstein, and L. Mathey, Nat. Phys. 9, 738 (2013).
[5] D. Greif, T. Uehlinger, G. Jotzu, L.Tarruell, and T. Esslinger,Science 340, 1307 (2013).
[6] D. Greif, G. Jotzu, M. Messer, R. Desbuquois, and T. EsslingerPhys. Rev. Lett.115, 260401 (2015).
[7] M. F. Parsons, A. Mazurenko, C. S. Chiu, G. Ji, D. Greif, and M. Greiner,Science 353, 1253 (2016).
[8] L. W. Cheuk1, M. A. Nichols, K. R. Lawrence, M. Okan, H. Zhang, E. Khatami, N. Trivedi, T. Paiva, M. Rigol, and M. W. Zwierlein,Science 353, 1260 (2016). [9] R. A. Hart, P. M. Duarte, T.-L. Yang, X. Liu, T. Paiva,
E. Khatami, R. T. Scalettar, N. Trivedi, D. A. Huse, and R. G. Hulet,Nature 519, 211214 (2015).
[10] J.H. Drewes, L.A. Miller, E. Cocchi, C.F. Chan, N. Wurz, M. Gall, D. Pertot, F. Brennecke, and M. K¨ohl, Phys. Rev. Lett.118, 170401 (2017).
[11] P. T. Brown, D. Mitra, E. Guardado-Sanchez, P. Schauss, S. S. Kondov, E. Khatami, T. Paiva, N. Trivedi, D. A. Huse, and W. S. Bakr,Science 357, 1385 (2017). [12] A. Mazurenko, C. S. Chiu, G. Ji, M. F. Parsons, M.
Kan´asz-Nagy, R. Schmidt, F. Grusdt, E. Demler, D. Greif, and M. Greiner,Nature 545, 462 (2017).
[13] W. S. Bakr, J. I. Gillen, A. Peng, S. F¨olling, and M. Greiner,Nature 462, 74 (2009).
[14] J. F. Sherson, C. Weitenberg, M. Endres, M. Cheneau, I. Bloch, and S. Kuhr,Nature467, 68 (2010).
[15] J. Simon, W. S. Bakr, R. Ma, M. E. Tai, P. M. Preiss, and M. Greiner,Nature 472, 307 (2011).
[16] T. Fukuhara, P. Schauss, M. Endres, S. Hild, M. Che-neau, I. Bloch, and C. Gross,Nature 502, 76 (2013). [17] T. Fukuhara, A. Kantian, M. Endres, M. Cheneau, P.
Schauss, S. Hild, D. Bellem, U. Schollw¨ock, T. Gia-marchi, C. Gross, I. Bloch, and S. Kuhr, Nat. Phys. 9, 235 (2013).
[18] T. Fukuhara, S. Hild, J. Zeiher, P. Schauss, I. Bloch, M. Endres, and C. Gross, Phys. Rev. Lett.115, (2015). [19] S. Hild, T. Fukuhara, P. Schauss, J. Zeiher, M. Knap,
E. Demler, I. Bloch, and C. Gross,Phys. Rev. Lett.113, 147205 (2014).
[20] M. W. Ray, E. Ruokokoski, K. Tiurev, M. M¨ott¨onen, and D. S. HallScience 348, 544 (2015).
[21] F. Pinheiro, G. M. Bruun, J.-P. Martikainen, and J. Lar-sonPhys. Rev. Lett.111, 205302 (2013).
[22] S. Sachdev, K. Sengupta, and S. M. Girvin, Phys. Rev. B 66, 075128 (2002).
[23] A. S. Buyskikh, L. Tagliacozzo, D. Schuricht, C. A. Hoo-ley, D. Pekker, and A. J. DaHoo-ley, arXiv:1811.06998. [24] F. Meinert, M. J. Mark, E. Kirilov, K. Lauber, P.
Wein-mann, A. J. Daley, and H.-C. N¨agerl, Phys. Rev. Lett. 111, 053003 (2013).
[25] F. Meinert, M. J. Mark, E. Kirilov, K. Lauber, P. Wein-mann, M. Gr¨obner, A. J. Daley, and H.-C. N¨agerl, Sci-ence 344, 1259 (2014).
[26] A. Kiely, J. G. Muga, and A. Ruschhaupt,Phys. Rev. A 98, 053616 (2018).
[27] S. Franke-Arnold, Phil. Trans. R. Soc. A 375 2087 (2017).
[28] C. Ryu, M. F. Andersen, P. Clad´e, Vasant Natarajan, K. Helmerson, and W. D. Phillips Phys. Rev. Lett.99, 260401 (2007).
[29] E. M. Wright, J. Arlt, and K. DholakiaPhys. Rev. A63, 013608 (2000).
[30] S. K. Schnelle, E. D. van Ooijen, M. J. Davis, N. R. Heckenberg, and H. Rubinsztein-Dunlop, Opt. Express 16, 1405-1412 (2008).
[31] K. Henderson, C. Ryu, C. MacCormick, and M. G. Boshier,New J. Phys.11, 043030 (2009).
[32] B. E. Sherlock, M. Gildemeister, E. Owen, E. Nugent, and C. J. Foot,Phys. Rev. A83, 043408 (2011). [33] A. S. Arnold,Opt. Lett.37, 2505 (2012).
[34] A. Turpin, J. Polo, Yu. V. Loiko, J. K¨uber, F. Schmaltz, T. K. Kalkandjiev, V. Ahufinger, G. Birkl, and J. Mom-part,Opt. Express23, 1638 (2015).
[35] A. Kumar, N. Anderson, W. D. Phillips, S. Eckel, G. K. Campbell, and S. Stringari,New J. Phys.18, 025001 (2016).
[36] I. Lesanovsky and W. von Klitzing,Phys. Rev. Lett.99, 083001 (2007).
[37] T. A. Bell, J. A. P. Glidden, L. Humbert, M. W. J. Brom-ley, S. A. Haine, M. J. Davis, T. W. Neely, M. A. Baker, and H. Rubinsztein-Dunlop, New J. Phys. 18, 035003 (2016).
[38] P. Navez, S. Pandey, H. Mas, K. Poulios, T. Fernholz, and W. von Klitzing,New J. Phys.18, 075014 (2016). [39] S. Beattie, S. Moulder, R. J. Fletcher, and Z. Hadzibabic
Phys. Rev. Lett.110, 025301 (2013).
[40] L. Corman, L. Chomaz, T. Bienaim´e, R. Desbuquois, C. Weitenberg, S. Nascimb`ene, J. Dalibard, and J. Beugnon
Phys. Rev. Lett.113, 135302 (2014).
[41] X. Li and W. V. Liu,Rep. Prog. Phys.79116401 (2016). [42] T. Kock, C. Hippler, A. Ewerbeck, and A. Hemmerich,
J. Phys. B: At. Mol. Opt. Phys.49, 042001 (2016). [43] J. Polo, J. Mompart, and V. Ahufinger,Phys. Rev. A93,
033613 (2016).
[44] R. J. Baxter,Exactly Solvable Models in Statistical Me-chanics (Academic, London, 1982).
[45] G. Gauthier, I. Lenton, N. McKay Parry, M. Baker, M. J. Davis, H. Rubinsztein-Dunlop, and T. W. Neely,Optica 3, 1136 (2016).
[46] A. Lizana, A. Vargas, A. Turpin, C. Ramirez, I. Estevez, and J. Campos,J. Opt.18, 105605 (2016).
[47] G. Pelegr´ı, A. M. Marques, R. G. Dias, A. J. Daley, V. Ahufinger, and J. Mompart Phys. Rev. A 99, 023612 (2019); G. Pelegr´ı, A. M. Marques, R. G. Dias, A. J. Daley, J. Mompart, and V. Ahufinger,Phys. Rev. A99, 023613 (2019).
[48] E. Ercolessi, S. Evangelisti, F. Franchini, and F. Ra-vanini,Phys. Rev. B 88, 104418 (2013).
[49] A. Isacsson and S. M. Girvin, Phys. Rev. A 72, 053604(2005).