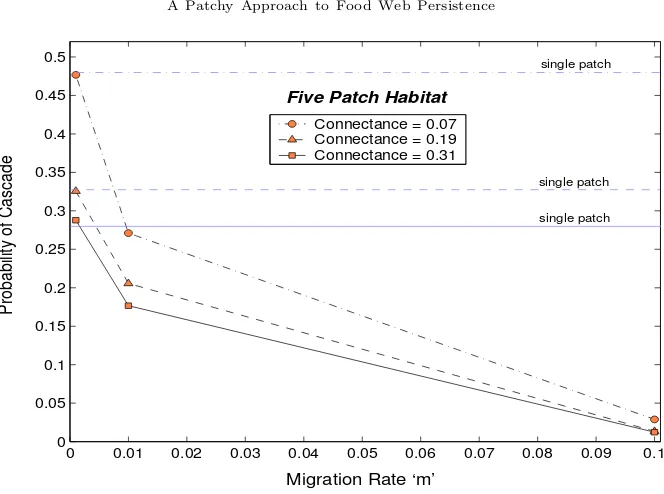
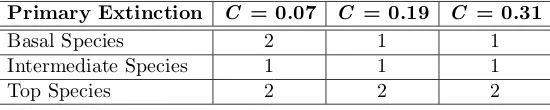
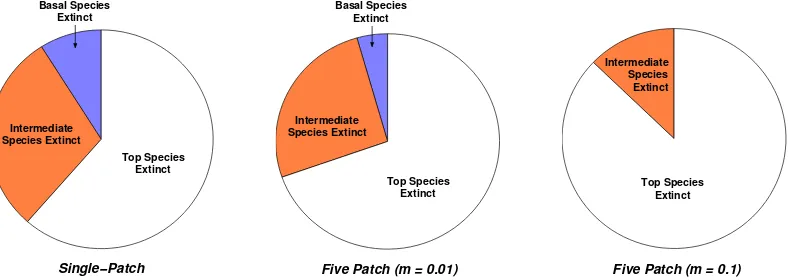
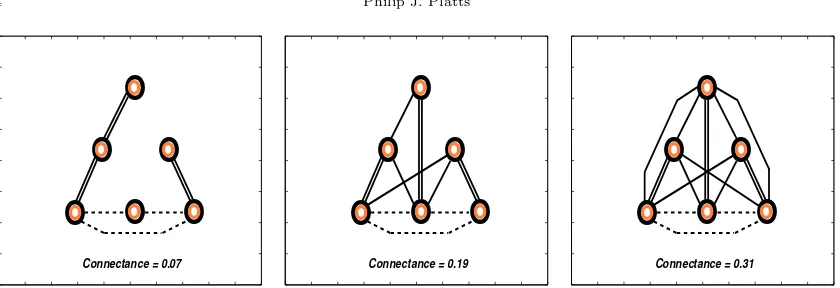
A patchy approach to food web persistence
Full text
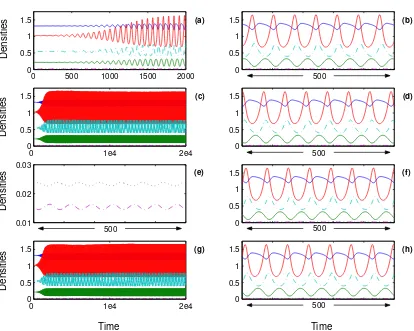
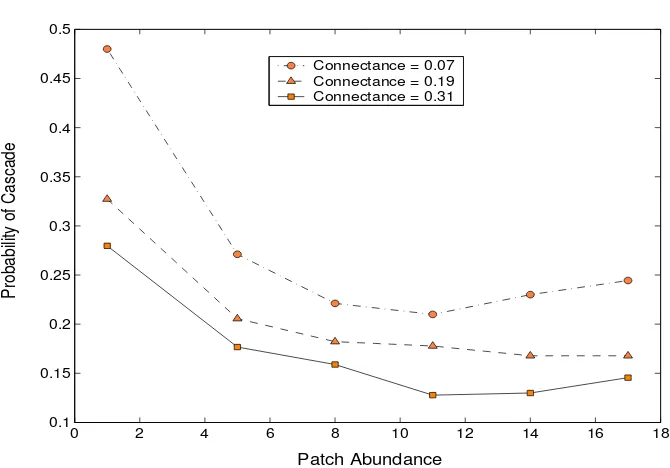
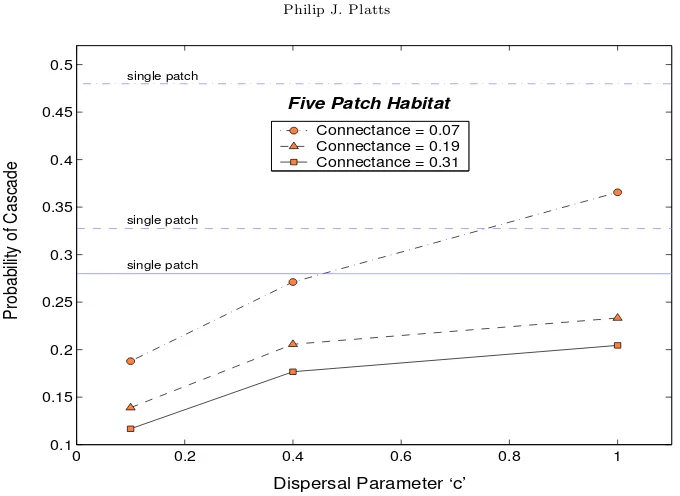
Figure
Related documents
2. made – God did the work, made the way c. This is a good description of God’s saving work a. David rejoices in this everlasting covenant 2. He will make it increase.. Follow flow
The instrument contained 13 attitudinal statements related to the newsletter received, measured on a seven-point Likert scale: reactions to the site (newsletter frequency, drop
(ENG) TÍTOL ACTIVITAT 8: : LABORATORI DE DISSENY D'OSCIL·LADORS DE RF Guided activities: 1h 30m Self study: 4h Guided activities: 2h Self study: 5h Guided activities: 1h
time spent building rapport was found to significantly influence payment type and amount of a..
Conversely, if the acceptor molecule (A) is sensitive to light, a similar excited species may be generated; this reagent reacts as a potent single electron oxidant and
In a model of sovereign borrowing and lending—a model with asym- metric information, costly state disclosure, and no court to enforce repayment—I show that a sovereign
Individual medical schools will ask you later on to submit a form or letter from your undergraduate school verifying that your report is accurate, often referred to as a “Dean
Guide to Graduate Education | 14 Academic Year 2014-15 along with the student’s application to the current program, the student must contact the Division of Graduate Studies