Design, Analysis, And Computational Methods For Engineering Synthetic Biological Networks
Full text
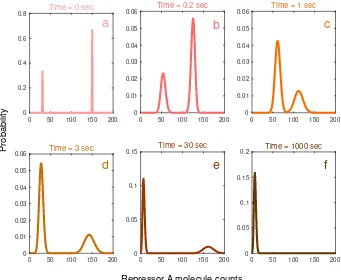
Figure
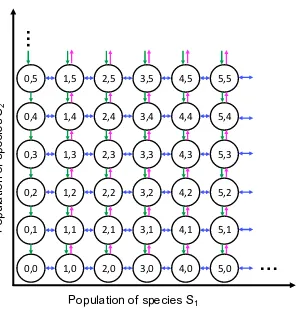
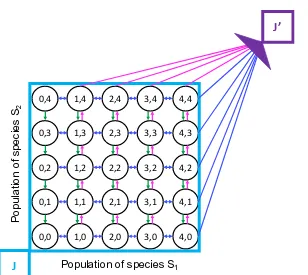
Related documents
Corpus Christi, The Naples of America, located on coast of Corpus Christi Bay 250 miles southwest of Houston, is entered by three railroads, elevation the highest on Texas
The Project Mana g er is responsi b le for the daily mana g ement of the project within the framework provided b y the Project Board, and is therefore responsi b le for the
Data from 135 countries covering five decades suggests that creditless recoveries, in which the stock of real credit does not return to the pre-crisis level
Methods for computing evolutionary distances that take into account the nucleotide (or amino acid) frequency bias for correcting multiple substitutions assume that the pattern
treatment (reducing) (AVT[R]); American Society of Mechanical Engineers (ASME); coal-fired power plants; chemistry guidelines; commercial operation; condensate polishers;
There are three programs in Prince Georges County Circuit Court to assist self represented litigants – the Family Division Information and Referral Center (FDIRC), the Pro
We focused on these two forms of heterogeneity because they re‡ect structural features of the sectors, such as price stickiness, the elasticity of demand and the returns to labor,
program recruits students from a highly-competitive national/international market in which many students are planning careers as graduate research faculty in leading university
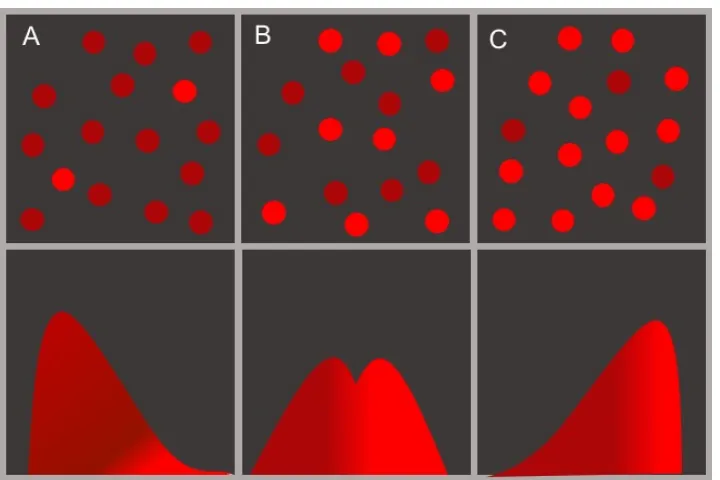
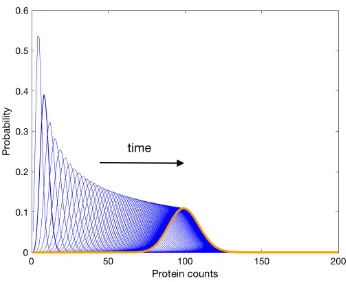
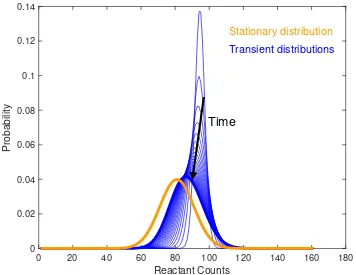
![Figure 2.8: The biological circuit diagram for the genetic toggle switch adaptedfrom [GCC00]](https://thumb-us.123doks.com/thumbv2/123dok_us/8107787.235553/45.612.122.471.94.379/figure-biological-circuit-diagram-genetic-toggle-switch-adaptedfrom.webp)