The importance of habitat quality for marine reserve fishery linkages
Full text
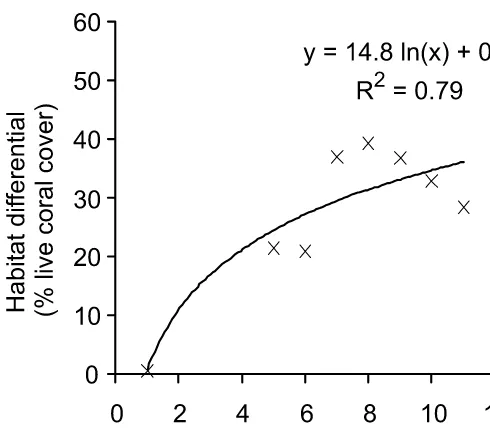
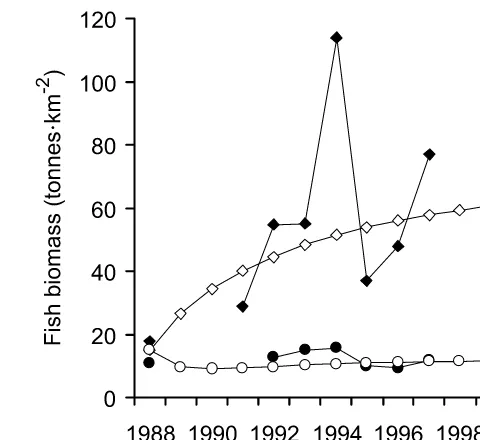
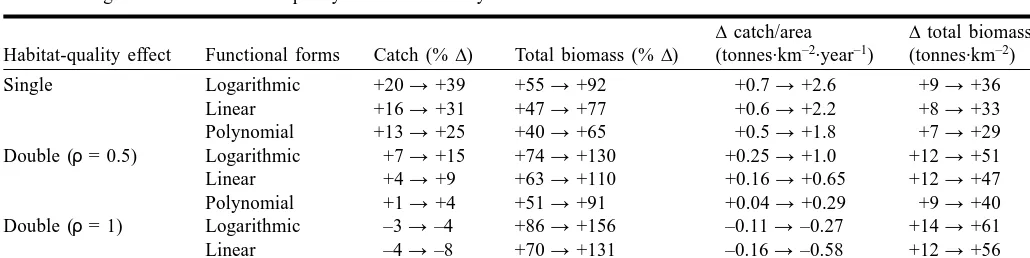
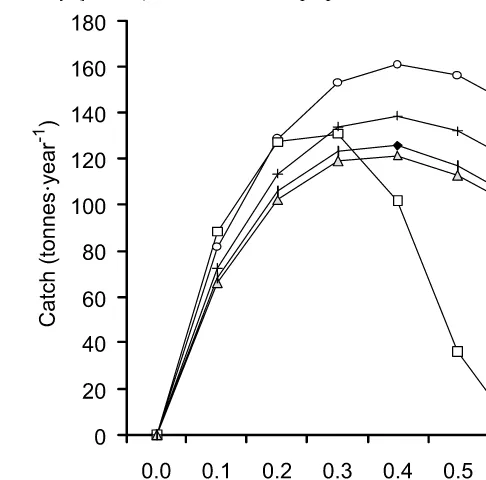
Figure
Related documents
Abstract: This study examines the unique experience of participants who during their reintegration back into the community, following a conviction for sexual offending, re-
Field experiments were conducted at Ebonyi State University Research Farm during 2009 and 2010 farming seasons to evaluate the effect of intercropping maize with
Cest cet aspect que nous allons maintenant analyser a partir de deux mesures de la consommation agregee d'energie, une mesure thermique, soit la fommle (I) et une mesure
But that is Marx’s exact point in discussing the lower phase of communism: “Right can never be higher than the economic structure of society and its cultural development which
The purpose of our study was threefold; first, to pro- vide a review of the extant literature on DDs and vio- lent behavior; second, to describe the prevalence of recent
The results of this study showed that in 2010, in France, about 1 to 10 patients managed for primary lung cancer in the respiratory department of a general hospital died within 1
In addition, results of our exploratory analyses suggest that exposure to specific microbes (e.g., lactobacilli and bifidobacteria) in the maternal vaginal flora may influence
BF-CBT: Biofeedback supported CBT; BMI: Body mass index; CBT: Cognitive behavioral therapy; CI: Confidence interval; DIGNITY: Danish Institute against Torture; DSM-IV: Diagnostic
