A point particle model of lightly bound skyrmions

ScienceDirect

Nuclear Physics B 917 (2017) 286–316

www.elsevier.com/locate/nuclphysb

A

point

particle

model

of

lightly

bound

skyrmions

Mike Gillard

_,

_{Derek Harland}

_,

_{Elliot Kirk}

_,

_{Ben Maybee}

_,

Martin Speight

a_{SchoolofMathematics,UniversityofLeeds,LeedsLS29JT,UK}

b_{TheWolfsonSchoolofEngineering,UniversityofLoughborough,LoughboroughLE113TU,UK} c_{DepartmentofMathematicalSciences,UniversityofDurham,DurhamDH13LE,UK}

Received 6January2017;accepted 31January2017 Availableonline 16February2017

Editor: StephanStieberger

Abstract

A simple model of the dynamics of lightly bound skyrmions is developed in which skyrmions are replaced by point particles, each carrying an internal orientation. The model accounts well for the static energy minimizers of baryon number 1 ≤B≤8 obtained by numerical simulation of the full field theory. For 9 ≤B≤23, a large number of static solutions of the point particle model are found, all closely resembling size Bsubsets of a face centred cubic lattice, with the particle orientations dictated by a simple colouring rule. Rigid body quantization of these solutions is performed, and the spin and isospin of the corresponding ground states extracted. As part of the quantization scheme, an algorithm to compute the symmetry group of an oriented point cloud, and to determine its corresponding Finkelstein–Rubinstein constraints, is devised. ©2017 The Author(s). Published by Elsevier B.V. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/). Funded by SCOAP3_.

1. Introduction

The Skyrme model isan effective theory of nuclearphysicsinwhich nucleonsemergeas topologicalsolitonsinafieldwhosesmall amplitudetravellingwavesrepresentpions. Itthus providesaunifiedtreatmentofbothnucleonsandthemesonswhich,intheYukawapicture,are responsibleforthestrongnuclearforcesbetweenthem.WhiletheSkyrmemodelhasbeen su-percededasafundamentalmodelof stronginteractionsbyQCD,interestinthemodelrevived

* _{Correspondingauthor.}

E-mailaddress:speight@maths.leeds.ac.uk(M. Speight). http://dx.doi.org/10.1016/j.nuclphysb.2017.01.027

onceitwasrecognizedtobeapossiblelowenergyreduction ofQCDinthelimitoflargeNc

(numberofcolours)[17,16],andmuchworkhasbeenconductedtoextractphenomenological predictionsaboutnucleifromstandardversionsofthemodel[11,12,10,3].Manyofthese predic-tionsareingoodqualitativeagreementwithexperiment,andrecentimprovementsinskyrmion quantizationschemesofferhopeofsignificantfurtherimprovementtocome[6,7].

Oneareainwhichstandardversionsofthemodelperformpoorly,however,isthatofnuclear bindingenergies:typically,classicalskyrmionsaremuchmoretightlyboundthanthenucleithey aremeanttorepresent(byafactorof15orso).Inrecentyears,nofewerthanthreevariantsof themodelhavebeenproposedwhichseektoremedythisproblem.Ineachcase,themodelis, bydesign,asmallperturbationofaSkyrmemodelinwhichthebindingenergiesvanishexactly. Perhapsthe mostradicalproposal, duetoSutcliffeandmotivatedby holography,couplesthe Skyrmefieldtoaninfinitetowerofvectormesons[15].Smallbutnonvanishingbindingenergies are(conjecturally)introducedbytruncatingthisinfinitetoweratsomehighbutfinitelevel.This proposal,whileelegant,hassofarnotbeenamenabletodetailed analysis.Asecondproposal, duetoAdam,Sánchez-GuillénandWereszczy´nski,startswithamodelwhichisinvariantunder volumepreservingdiffeomorphismsofspace,thenperturbsitbymixingwithasmallfractionof theconventionalSkyrmeenergy[1].Skyrmionsinthismodelhavetheattractivefeatureofbeing somewhatakintoliquiddrops.However,thelarge(infact,infinitedimensional)symmetrygroup oftheunperturbedmodelisextremelyproblematicfornumericalsimulations,andtheshapesand symmetriesof classicalskyrmions,evenforratherlowbaryonnumber(B≥3)are,sofar,not knowninthismodelintheregimeofrealisticallysmallbindingenergy[5].

Inthispaperwewillstudythethird(andarguablyleastradical)proposal,originallyduetoone ofus[8].ThisamountstomakinganonstandardchoiceofpotentialterminthestandardSkyrme lagrangianand,moreimportantly,radicallyshiftingtheweightingofthederivativetermsfrom thequadratictothequartic.Theresultingmodelisstillamenabletonumericalsimulation,but itsclassicalsolutionsarequitedifferentfromconventionalskyrmions:thelowestenergySkyrme fieldofbaryonnumberBnowresemblesalooselyboundcollectionofBsphericallysymmetric unit skyrmions, ratherthan a tightly bound objectin whichthe skyrmions have mergedand losttheirindividualidentities.Intheterminologyof[14],whichstudieda(2+1)-dimensional analogueofthemodel,skyrmionsinthislightlyboundSkyrmemodelprefertoholdthemselves alooffromoneanother.Numericalanalysisreveals[5]thattheyalsoprefertoarrangethemselves ontheverticesofafacecentredcubicspatiallattice,withinternalorientationsdictatedbytheir latticeposition.Thissuggeststhat,unlikeconventionalskyrmions,lightlyboundskyrmionscan bemodelledaspointparticles,eachcarryinganinternalorientation,interactingwithoneanother throughsomepairwiseinteractionpotentialwhoseminimumencouragesthemtositatafixed separation withtheir internal orientationscorrelated.The aim of thispaper is toderive such asimplepoint particlemodel, compare itspredictions with numericalsimulationsof the full fieldtheory, anduse it to extract, via rigid body quantization,phenomenological predictions aboutnucleiwithbaryonnumber2≤B≤23.Asimilarprogramme(minusquantization)forthe (2+1)-dimensional analoguemodelwascompletedin[14].

determinedbyadhocmeans:onelooksatsuitablepicturesoftheskyrmion,predictsasymmetry byeye,thenchecksitbyoperatingonthenumericaldata.Bycontrast,we willdevelopan al-gorithmwhichautomaticallycomputesthesymmetrygroupofanypointparticleconfiguration. Thisallowsustocompletelyautomatetherigidbodyquantizationscheme.Theresultis,asa phenomenologicalmodel ofnuclei, moderatelysuccessful:rigid bodygroundstates plausibly accountforthelightestnucleusofbaryonnumberBfor12ofthe23valuesconsidered. Presum-ablythiscanbeimprovedbyreplacingrigidbodyquantizationbysomethingmoresophisticated. Therestofthepaperisstructuredasfollows.Insection2wereviewthelightlyboundSkyrme model, focusing onits spin–isospinsymmetryandassociated inertia tensors. Insection 3 we introducethepointparticlemodel,theninsection4wedescribeanumericalschemetofindits energy minimizers,andpresentthe resultsof thisscheme.Insection5 weformulatetherigid bodyquantizationofourclassicalenergyminimizers,focusing particularlyontheFinkelstein– Rubinsteinconstraints.Someconcludingremarksandpossiblefuturedirectionsofdevelopment arepresentedinsection6.

2. The lightly bound Skyrme model

Thefieldtheoryofinterestisdefinedasfollows.ThereisasingleSkyrmefieldU:R3,1→ SU(2),requiredtosatisfytheboundaryconditionU (t,x)=1 as|x|→ ∞forallt.Suchafield, ifsmooth,hasateacht,awell-definedintegervaluedtopologicalcharge

B= − 1

24π2

R3

ij kTr(RiRjRk)d3x, (2.1)

thetopologicaldegreeofthemapU (t,·):R3∪ {∞}→SU(2)∼=S3.Sincethefieldissmooth, B(t ) issmoothandintegervalued, henceautomaticallyconserved.Physically itisinterpreted as the baryonnumberof the field U. The rightinvariant current associated withU isRμ= (∂μU )U†,intermsofwhichthelagrangiandensityis

L= Fπ2

16h_¯Tr(RμR

μ_{)+ ¯}h

32e2Tr([Rμ, Rν],[R

μ_{, R}ν_])

−Fπ2m2π

8h_¯3 Tr(1−U )−

F_π4e2α 32(1−α)2(

1

2Tr(1−U )) 4_.

(2.2)

HereFπ isthepiondecayconstant,mπ thepionmass,ande >0,0≤α <1 aredimensionless

parameters.In[5]thefollowingvalueswerechosenfortheseparameterssothatclassicalbinding energiesinthemodelarecomparablewithexperimentally-measurednuclearbindingenergies1:

Fπ=36.1 MeV, mπ=303 MeV, e=3.76, α=0.95. (2.3)

Thereiscertainlyroomforimprovementinthiscalibration:forexample,obtainingthecorrect pionmasswasnotapriorityin[5],andweexpectthatamorethoroughanalysiscouldresultina parametersetforwhichmπ isclosertoitsexperimentalvalueof137 MeV.However,theaimin

thepresentpaperisnottofine-tunetheparameters,butrathertostudyqualitativepropertiesof staticsolutions,whichweexpecttobeinsensitivetodetailsofthecalibration.

1 _{Thevaluefor F}

ItwillbeconvenienttouseFπ/4e

√

1−αasaunitofenergyand2√1−α/Fπeasaunitof

length;intheseunitsthelagrangiantakestheformL=T −V,where

T =

R3

−1

2(1−α)Tr(R0R0)− 1

8Tr([R0, Ri][R0, Ri])

d3x, (2.4)

V =

R3

(1−α)

−1

2Tr(RiRi)+m 2

Tr(1−U )

− 1

16Tr([Ri, Rj][Ri, Rj])+α( 1

2Tr(1−U ))

4_d3_{x, (2.5)}

andm:=(2mπ

√

1−α/Fπe).Intheparametersetgivenabove,m=1.00.Notethatwhenα=0, ListhelagrangianoftheconventionalSkyrmemodelwithpionmass,whileforα=1 thisisa completelyunboundmodel[8]:thereisatopologicalenergyboundoftheformV ≥const|B|, butthisisattainedonlywhen|B|≤1.

ThefirstapproximationtoanucleuscontainingBnucleonsisastaticSkyrmefieldU:R3→ SU(2)of degreeB whichminimizes the potential energy V.Thusit is importanttoidentify staticclassicalenergyminimizers.Thesearereferredtoasskyrmions.Abetterapproximationto anucleusisobtainedbyallowingsolitonstocarryspinandisospin.Thelagrangianisinvariant underaleftactionofthegroupG:=SU(2)I×SU(2)J,definedby

[(g, h)·U](t,x):=gU (t, h−1xh)g−1 (2.6)

wherewehaveidentifiedphysicalspaceR3withtheLiealgebrasu(2)via x ∼=ixjσj,σ1,σ2,σ3 beingthePaulimatrices,todefinetheactionofhon x.Equivalently,

[(g, h)·U](t,x):=gU (t, R(h)−1x)g−1 (2.7)

whereR(h)istheSO(3)matrixwithentries

R(h)ij=

1 2Tr(hσih

−1_σ

j). (2.8)

The conserved quantities associated withthese symmetriesare isospin and spin.Werefer to transformationsg∈SU(2)I asisorotations,inanalogywithrotationsh∈SU(2)J.

Everyω∈g:=su(2)I⊕su(2)J definesaone-parametersubgroup{exp(tω) : t∈R}of G

isomorphictoS1,whoseactiononastaticskyrmionUgeneratesarigidlyisorotatingand rotat-ingskyrmion,Uω=exp(tω)·U,ofconstantkineticenergyT[Uω].Themappingω→T[Uω]is

aquadraticformong,andhencedefinesauniquesymmetricbilinearform :g×g→Rcalled the inertia tensoroftheskyrmionU.Byitsdefinition, vanishesonthesubspaceofgtangent totheisotropygroupGU ofU(thatis,thesubgroupGU := {(g,h)∈G : (g,h)·U=U}< G whichleavesU unchanged).IfGU _{isdiscrete,as isthecasefor allthe skyrmionsstudiedin}

consistentlyrepresentinertiatensorsinthisway,havingchosenthebasis[−₂iσ1,−₂iσ2,−₂iσ3] forsu(2).

3. The point particle model

Extensivenumericalsimulationsreportedin[5]showedthatskyrmionsinthelightlybound Skyrme modelwithB >0 invariablyresemblecollectionsof B particles.Encouraged bythis observation,wehavedevelopedapointparticlemodelinwhichaSkyrmefieldU withbaryon numberBisreplacedbyBorientedpointparticlesinR3_.

To explain how the model is derived, we begin by recalling the structure of the simplest skyrmion,whichhasB=1,andisof“hedgehog”form

UH(x)=exp(f (r)iσjxj/r), (3.1)

withf (r)arealfunctionsatisfyingf (0)=π,f (r)→0 asr→ ∞,andr= |x|.Theprofile functionisdetermined bysolving(numerically)the Euler–LagrangeequationforV restricted tofieldsofhedgehogform,acertainnonlinearsecondorderODEforf.OnefindsthatUH has

totalenergyMH:=V[UH]≈87.49,anditsenergydensityismonotonicallydecreasingwithr

andconcentratedaroundtheorigin.The1-skyrmionhasahighdegreeofsymmetry:ifg∈SU(2) then

gUH(R(g)−1x)g−1=UH(x).

Inotherwords,GUH _{isthediagonalsubgroupofSU(2)}

I×SU(2)J.

Thisbasicskyrmioncanbemovedandrotatedusingsymmetriesofthemodel.A1-skyrmion withposition x0∈R3andorientationq0∈SU(2)isgivenby

U (x;x0, q0)=UH(R(q0)(x−x0)). (3.2)

Theenergy-minimizerswith2≤B≤8 resemblesuperpositionsoffieldsofthistype[5].More precisely,theirenergydensitiesareconcentratedatBwell-separatedpoints x1,. . . ,xB,andnear eachsuchpoint xathefieldUisapproximatelyoftheaboveformforsomeqa.Thesepositions

andorientationsarethebasicdegreesoffreedominourpointparticlemodel,andwillbeallowed todependontimet.Thelagrangianforthispointparticlemodeltakestheform

Lpp= B

a₌1

1 2M|˙xa|

2₊1 2L| ˙qa|

2

−BM−V (x1, . . . ,xB, q1, . . . , qB), (3.3)

where| ˙q|2:=1₂Tr(q˙q˙†)and

V (x1, . . . ,xB, q1, . . . , qB)=

1≤a<b≤B

Vint(xa, qa,xb, qb), (3.4)

isaninteractionpotential.

Thetermsinvolvingtimederivativesof xa andqa representthekineticenergy ofamoving

skyrmion. Their coefficients could be deducedfrom the Skyrme model.It is known that the 1-skyrmionhasinertiatensor

H=LH

Id3 −Id3

−Id3 Id3

,

LH=

16π 3

∞

0

sin2f(1−α)r2+r2(f)2+sin2f dr≈53.49.

Fromthisitfollowsthatthekineticenergyofarigidlyrotatingskyrmionshouldtaketheform 1

2LH| ˙q0|2, suggestingthat L=LH inthe lagrangian(3.3).Similarly, thekineticenergy of a 1-skyrmionmoving withvelocityx˙0is 1₂MH|˙x0|2,whereMH ≈87.49 isthepotentialenergy

ofastatic1-skyrmion.ThissuggestschoosingM=MH inthelagrangian.However,wehave

chosentofixthecoefficientsbyanalternativephenomenologicalmethodthatwillbeexplained inthenextsection.

3.1. Symmetries of the interaction potential

ThepointparticlemodelinheritsanactionofG=SU(2)I×SU(2)J fromtheSkyrmemodel.

Theactionof(g,h)∈GonthefieldU (x;x0,q0)definedinequation(3.2)is U (x;x0, q0)→gU (R(h)−1x;x0, q0)g−1

=gUH(R(q0)(R(h)−1x−x0))g−1

=UH(R(g)R(q0)R(h)−1(x−R(h)x0))

=U (x;R(h)x0, gq0h−1).

Thereforetheactionof(g,h)onapointparticleconfigurationis

(xa, qa)→(R(h)xa, gqah−1), a=1, . . . , B.

Thepointparticlelagrangianshouldbeinvariantunderthesetransformations,andunder transla-tions xa→xa+cfor c ∈R3.Itshouldbeinvariantunderchangesofthesignsofanyoftheqa,

becauseU (x;x0,−q0)=U (x;x0,q0).Itshouldalsobeinvariantunderpermutationsofthe par-ticles,becauseconfigurationsofparticlesthatarethesameuptoare-orderingdescribethesame Skyrmefield.Finally,theSkyrmemodelisinvariantundertheinversion

U (x)→U (−x)†,

whichisequivalent,forafieldoftheform(3.2),to(x0,q0)→(−x,q0).Hence,ourpointparticle lagrangianshouldbeinvariantunder

(xa, qa)→(−xa, qa). (3.5)

Thekinetictermsin(3.3)obviouslyhavethesesymmetries.Demandingthatthepotential(3.4)

isalsoinvariantimposesconstraintsonthefunctionVint(x1,q1,x2,q2)whichwenowdescribe. Translation symmetry implies that Vint(x1,q1,x2,q2) depends on the positions of the skyrmionsonlythroughtheirrelativeposition X :=x1−x2.Isorotationsymmetryimpliesthatit dependsonq1,q2onlythroughtheisorotation–invariantcombinationQ=q1−1q2.Thus

Vint(x1, q1,x2, q2)=Vred(X, Q),

forsomefunctionVred onR3\{0}×SU(2).Invarianceunderq1→ −q1implies

Vred(X,−Q)=Vred(X, Q), (3.6)

whilerotationalsymmetrydemandsthat

Apermutation(x1,q1,x2,q2)→(x2,q2,x1,q1)changesthesignof XandinvertsQ,so permu-tationinvarianceimpliesthat

Vred(−X, Q−1)=V (X, Q). (3.8)

Finally,symmetryunderinversion(3.5),implies

Vred(−X, Q)=Vred(X, Q). (3.9)

Toproceedfurther,itishelpfultothinkofVred asaone-parameterfamilyofrealfunctions VρonS2×SU(2),parametrizedbyρ:= |X|∈(0,∞).Wemayexpandeachsuchfunctionina

convenientbasisforL2(S2×SU(2)),forexample,thebasisofeigenfunctionsoftheLaplacian. Anaturaltruncationtofinitedimensionsisobtainedbykeepingonlyeigenfunctionsuptoafixed finiteeigenvalue.TheeffectofthistruncationistoexcludefromVred termswithfastorientation

dependence.Thismotivatesthefollowingdefinition:foreachλinthespectrumof_S2_×S3,let Eλdenotethecorrespondingeigenspace,andforanyμ≥0,

Fμ=

λ≤μ

Eλ. (3.10)

LetC_μ∞denotethespaceofsmoothfunctionsonV :R3_{\{0}×SU(2)→RsuchthatV}

ρ∈Fμ

forallρ.

Proposition 1. Let μ∈ [0,20) and V be a function in C_μ∞ invariant under the symmetries

(3.6)–(3.9). Then there exist functions Vi:(0,∞)→R, i=0,1,2, such that

V (X, Q)=V0(|X|)+V1(|X|)Tr(R(Q))+V2(|X|)

X·R(Q)X

|X|2 . (3.11)

Proof. RecallthattheeigenvaluesoftheLaplacianonSnareλ(n)_d =d(d+n−1),d=0,1,2,. . ., andthecorrespondingeigenspaces,E(n)_d ,arespannedby(therestrictionstoSn⊂Rn+1of) har-monic homogeneous polynomialsin Rn+1_{of degree d [2]. Itfollows that the eigenvaluesof S}2_×S3 areλ_d(2)+λ(_d3) witheigenspacesE_d(2)⊗E(_d3).By(3.6),(3.9),V isinvariantunderboth X → −XandQ→ −Q,sowemayrestrictdanddtoonlyevenvalues(homogeneous polyno-mialsofodddegreeareparityodd).Further,sinceV ∈C_μ∞withμ<20,eachrestrictionVρ lies

in

E0⊕E6⊕E8⊕E14=(E₀(2)⊗E(₀3))⊕(E(₂2)⊗E₀(3))⊕(E(₀2)⊗E(₂3))⊕(E(₂2)⊗E(₂3)). (3.12)

Now SU(2)acts onboth E(_d2) (byrotations of S2)andE(_d3) (byconjugationon SU(2)),and, by(3.7),each Vρ isinvariantunderthecombinedaction.InfactE(_d2)∼=R2d+1andcarriesthe

irreducible spin d representation of SU(2),while E(_d3)∼=Rd+1⊗Rd+1 where, for d=2, Rd+1_{carriestheirreduciblespinrepresentationofSU(2).Inparticular,E}(3)

0 =R,onwhich SU(2)actstrivially,andE₀(3)decomposesintoirreduciblerepresentationsas

E(3)

0 =R⊕R 3_⊕R5_.

(3.13)

inthethree-dimensionalspace spannedbythese.Clearly Etriv₀ =E0whichisspannedby the constantfunction(X,Q)→1.Considerthefunctions

(X, Q)→Tr(Q), (X, Q)→X·R(Q)X−1

2TrR(Q)|X| 2_.

(3.14)

ThesearemanifestlySU(2)invariantandextendtohomogeneouspolynomialsonR3×R4of bidegree (0,2) and(2,2) respectively. Furthermore, one mayreadily check that these poly-nomialsare harmonic (separatelywithrespect toXandQ).Hence,theyspanE₈triv andE₁₄triv respectively.Notingthat|X|2≡1 onS2,theclaimfollows. 2

Fromnowon,weassumethatVredliesinthetruncatedfunctionspaceC₁₄∞,sothatithasthe

structureprescribedbyProposition 1.

Recall that, in the standard Skyrme model, the interaction potential for well separated skyrmion pairs can be modelled using the dipole formalism [13]: far from its centre, a unit skyrmionlookslikethefieldinducedinthelinearizationoftheSkyrmemodelaboutthevacuum, U=1,byanorthogonaltripletofscalardipolesplacedattheskyrmion’scentre.Theinteraction potentialforaskyrmionpairwithrelativeposition XandorientationQcanthenbeapproximated bytheinteractionenergyofapairoftripletsofdipolesheldatrelativedisplacement Xand orien-tationQ,interactingviathelineartheory.Thisapproximationintroducesanotherusefulconstant associatedwiththeunitskyrmion,namelythestrengthofthe(necessarilyequal)dipoles.In prac-ticethisisdeterminednumericallybyreadingoffacoefficientCinthelargerasymptoticsofthe skyrmionprofilefunction.ThisformalismisreadilyadaptedtothelightlyboundSkyrmemodel, producinganinteractionpotentialoftheform(3.11)with

V0(r)=0

V1(r)= −8π C2(1−α)

m r2+

1 r3

e−mr

V2(r)=8π C2(1−α)

m2

r +

3m r2 +

3 r3

e−mr. (3.15)

The dipole strength (for α=0.95 and m=1) isfound numerically tobe C ≈14.58. These formulaereproducetheusualpredictionofattractiveandrepulsivechannelsforwell-separated skyrmions.Thatis,Vred ismaximallyattractive(increasesfastestwith|X|)iftheorientations

ofthe skyrmionsdifferbyarotationby π aboutany directionorthogonalto X,ismaximally repulsiveiftheorientationsdifferbyarotationbyπ about X,andisnonmaximally repulsive iftheirorientationsareequal.Werefertothesethreesituationsastheattractive,repulsiveand productchannelsrespectively.

TheexistenceofthesethreechannelsallowsustofixthefunctionsV0,V1,V2numericallyby conductingscatteringsimulationsofskyrmionpairsinthefullfieldtheory,insimilarfashionto SalmiandSutcliffe’sworkonthe(2+1)-dimensional model[14].WebeginwithaSkyrmefield oftheform

Ua(x1, x2, x3)=UH(x1+ s

2, x2, x3)UH(−(x1− s

2),−x2, x3) (3.16) wheres >0 is largeandUH is aunit hedgehogskyrmion defined (numerically)ina ballof

radiuslessthans/2 (soUH(x)=1 forall|x|≥s/2,andtheproductabovecommutes).Sucha

R3_{→SU(2)tobethosepointswhereU= −1.WenowallowUtoevolvewithtimeaccording} to the dynamics defined by the lagrangian (2.2), using the fourth orderspatial discretization employedbytheenergyminimizationschemeof[5],andafourthorderRunge–Kuttascheme withfixedtimestepforthetimeevolution.ThisnumericalschemeconservedtotalenergyE= T +V toextremelyhighaccuracy,

max

t

|E(t )−E(0)|

E(0) <2.4×10

−5_{, (3.17)}

forallthedynamicalprocessespresentedhere.Asthedipolemodelpredicts,theskyrmionswith theseinitialdata slowlymovetowardsoneanother,attainaminimum separation,thenrecede again.Byrecordingtheirseparations(t)andpotentialenergyV (t)ateachtimestep,werecover a numericalapproximation tothe attractive channelinteraction potential which, accordingto

(3.11)isrelatedtoV0,V1,V2by

Va(s)=V0(s)−V1(s)−V2(s). (3.18)

Wethenrepeattheprocesswithinitial data

Ur(x1, x2, x3)=UH(x1+ s

2, x2, x3)UH(−(x1− s

2), x2,−x3) (3.19) Up(x1, x2, x3)=UH(x1+

s

2, x2, x3)UH(x1− s

2, x2, x3) (3.20) whichareintherepulsiveandproductchannelsrespectively.Tomaketheskyrmionsapproach oneanotherandinteract,wenowGalileanboostthemtowardsoneanotheratlowspeed(v=0.1). Notethatthereflexionsymmetriesoftheinitialdatatrapthesefieldsintheirrespectivechannels foralltime.Fromthesenumericalsolutionsweobtainnumericalapproximationstotherepulsive andproductchannelinteractionpotentials,whicharerelatedtoV0,V1,V2by

Vr(s)=V0(s)−V1(s)+V2(s), (3.21)

Vp(s)=V0(s)+3V1(s)+V2(s). (3.22)

ItisclearthatVa,Vr,VpuniquelydetermineV0,V1,V2andhence,withintheansatz(3.11),Vint.

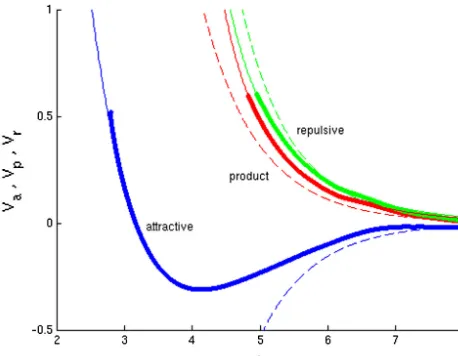
Graphs of Va,Vr,Vp,determinednumerically as described above,are presentedinFig. 1.

These curves also show the potentials predicted by the dipole model (with dipole strength C=14.58).Clearly,thedipoleformulae(3.15)do notprovideanaccuratequantitativepicture ofskyrmioninteractionsinthelightlyboundmodelatanyseparationwheretheinteractionsare notnegligible.Thisis,perhaps,notsurprising,sincethedipoleformalismreplacesthefullfield theorybytermsoriginatingonlyinthequadraticandpionmasspotentialtermsofthelagrangian, andthesearepreciselythetermswhicharegivenverylowweighting,1−α,inthelightlybound regime.Thequalitativepredictionsofthedipolepicturearereliablehowever:theinteraction po-tentialsappeartodecayexponentiallyfast,andthethreechannelsidentifiedhavethebehaviour predicted(attractive,repulsive,moreweaklyrepulsive).Forlateruse,itisconvenienttohave explicitfunctionswhichapproximatethenumericaldatafor Va,Vr,Vp.Forourpurposes,itis

importantthatthesefunctionsdecayexponentiallywithsandaccuratelyfitthenumericaldata fors≥s0,wheres0issomewhatsmallerthentheequilibriumseparationdefinedbyVa(thatis,

Fig. 1.Interactionenergiesofskyrmionspairswithseparation s intheattractive(blue),product(red)andrepulsive (green)channels.Ineachcasethethickcurverepresentsnumericaldataextractedfromascatteringprocess,thethin curveisafittothis,andthedashedcurveistheinteractionenergypredictedbythedipolemodel.(Forinterpretationof thereferencestocolorinthisfigurelegend,thereaderisreferredtothewebversionofthisarticle.)

Va(s)=

7.7479₋4.5997s₊0.8297s2_−0.0473s3

1−0.4751s+0.0843s2_+0.0331s3_−0.0049s4 0≤s <7.096

−94.6178e−_ss s≥7.096,

Vr(s)=

2476

s −

20322 s2 +

50254 s3

e−s,

Vp(s)=

2126

s −

18325 s2 +

47298 s3

e−s.

(3.23)

Ofthese,themostelaborateisVa,aPadéapproximanton[0,7.096]splicedtoanexponentially

decayingtail,the splicebeingchosensothat Va iscontinuously differentiable.UnlikeVr and Vp, Va is welldefined at s=0, where it is chosento equal the staticenergy of the axially

symmetric B=2 solution (asaddle pointof the Skyrme energy), obtainednumerically bya differentscheme,achoicemademainlyforaestheticreasons.

Fromnowon,wechooseVred tobethefunctiondefinedby(3.11),where

V0(s)= 1

2Va(s)+ 1

4Vp(s)+ 1 4Vr(s)

V1(s)= 1

4Vp(s)− 1 4Vr(s)

V2(s)= − 1

2Va(s)+ 1 2Vr(s)

andVa,Vp,Vrarethefunctionsdefinedin(3.23).Itisstraightforwardtoshowthatthisfunction Vred isboundedbelowas,onphysicalgrounds,itshouldbe.

3.2. The FCC lattice

WehaveseenthattheinteractionpotentialVint prefersparticlestobeintheattractive

totheirlineofseparationthroughangleπ.Itisthereforedesirabletofindawaytopackthem together such that all neighbouringpairs of particlesare in the attractive channel. The face-centred-cubic(FCC)latticeprovidesasolutiontothisproblem.

Theface-centredcubiclatticemaybedefinedtobe

{(n1λ, n2λ, n3λ): n∈Z3, n1+n2+n3=0 mod 2},

withλ>0 definingalatticescale.Theunderlyingcubiclatticeisgivenbypoints(n1λ,n2λ,n3λ) forwhichn1,n2,n3arealleven.Thosepointsforwhichsomeofthecoordinatesni areoddlie

onfacesoftheunderlyingcubiccells.

Weassignorientationstothesepointsasfollows:thosepointsontheverticeshaveorientation 1∈SU(2),thoseonfacesperpendiculartothex-axishaveorientation i,thoseonfaces perpen-diculartothey-axishaveorientation j,andthoseperpendiculartothez-axishaveorientation k. Herewe haveimplicitlyidentifiedelementsq∈SU(2)withunitquaternionsq∈H,suchthat

i = −iσ1, j = −iσ2, k = −iσ3and1 istheidentitymatrix.Putdifferently,theorientationqofa particleatlatticesite(n1,n2,n3)λissuchthat

R(q)=

⎛ ⎜ ⎝

(−1)n1 0 0

0 (−1)n2 ₀

0 0 (−1)n3 ⎞ ⎟ ⎠.

Thereadermayverifythatanypairofnearestneighbours,separatedbyadistanceλ√2,isinthe attractivechannel.

Onemightexpectthatminimizersofthepotentialenergyderivedfrom(3.3)resemblesubsets oftheFCClattice.ThiswascertainlytrueofallglobalminimaoftheSkyrmeenergyidentified in[5],andallbutoneofthelocalminima.

3.3. Inertia tensors

Thepointparticlemodel(3.3)makessimplepredictionsfortheinertiatensorsoflightlybound skyrmions.Theseare obtainedbycalculatingthe kinetic energyof a rotatingandisorotating orientedpointcloud.

Let {(xa,qa)} beaminimizer of the potential energy derived from(3.3).Chooseany pair

ofangular velocities(ωI,ωJ)∈su(2)⊕su(2).It isusefultoidentifyeach ω∈su(2)witha

vectorω∈R3bychoosing−₂iσj,j=1,2,3,asabasisforsu(2)(soω= −₂iω·σ).Consider

the followingconfiguration,whichisisorotatingandrotatingatconstantangularvelocityω= (ωI,ωJ):

(xa(t), qa(t))=exp(ωt)·(xa, qa)

=(R(exp(ωJt ))xa,exp(ωIt )qaexp(−ωJt )) .

Wefind

˙

xa(0)=ωJ×xa,

˙

qa(0)=ωIqa−qaωJ=(ωI−qaωJqa−1)qa,

whence

|˙xa(0)|2= |ωJ|2|xa|2−(ωJ·xa)2,

| ˙qa(0)|2=

1

2Tr[(ωI−qaωJq

−1

a )qaqa†(ω

†

I−qaω

†

Jq−

1

a )]

Thereforethekineticenergyis

1 2

B

a=1

M|˙xa|2+L| ˙qa|2

=ωI ωJ

ωI ωJ

, (3.24)

wheretheinertiatensoris

=

B

a=1

M

03 03

03 |xa|2Id3−xaxTa

+L

Id3 −R(qa)

−R(qa)T Id3

. (3.25)

The pointparticlemodel predicts that thisis agood approximationto theinertia tensorof a lightlybounddegreeBskyrmion.Wewilltestthispredictioninthenextsection.

4. Energy minimizers in the point particle model

4.1. Light nuclei

Havingintroducedthe pointparticlemodel forlightlyboundskyrmions,inthissection we present ourresults for energy-minimizing configurationsof pointparticles. Webegin by dis-cussing ourresults for eightparticles or fewer, wherecomparison can be made withenergy minimainthelightlyboundSkyrmemodelfoundin[5].

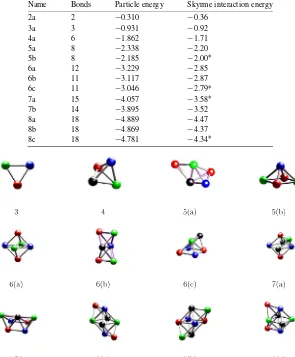
Wehavedevelopedaniterativezero-temperatureannealingalgorithmtominimizetheenergy of aconfigurationofparticles. Weappliedthisalgorithm bothtorandomly-choseninitial en-semblesofparticlesandtoinitialensemblesthataresubsetsoftheFCClattice.Weranalarge numberofsimulationsforeachvalueofB,typicallyobtainingseverallocalenergyminima,and recordhereonlythelowestlocalminimumanduptotwoclosestcompetitors.Energiesofthese localminimawith2≤B≤8 arepresented inTable 1.Theparticleensemblesthemselves are depictedinFig. 2.ThecorrespondingbindingenergiesinthelightlyboundSkyrmemodelare alsorecordedinthetable.ThesearedefinedtobetheenergyoftheB-skyrmionminusBtimes theenergyofthe1-skyrmion.

Our results are almost entirely consistent with the results obtained for the lightly bound Skyrmemodelin[5].For1≤B≤5 weobtainedthesameglobalminimaasinthelightlybound Skyrmemodel. ForB=6,7,8 multiplelocalminimawerepreviouslyobtainedinthelightly bound Skyrmemodel. Allof theseoccurred aslocal minimainthe pointparticlemodel.For B=7,8 theorderingofenergiesinthepointparticlealsoagreedwiththeorderingofenergies inthelightlyboundSkyrmemodel.Theonlyfailureofthepointparticlemodelisfor6particles: heretheenergiesofthetwolowest-energylocalminimaappearinthewrongorder.

In addition to reproducing previously-known minimizers from the lightly bound Skyrme modelourpointparticlemodelalsopredictedsomenewlocalminima.Mostinterestingly,the global energy-minimizerinthe pointparticlemodel for B=7, labelled 7ainFig. 2,did not correspondtoanysolutionofthelightlyboundSkyrmemodelfoundin[5].Basedonthis dis-covery,weconstructedanapproximateSkyrmefieldwithasimilarshapetothe pointparticle energy-minimizer,andminimizeditsenergyusingthesamenumericalschemethatwasusedin

Table 1

Energies and numbers of bonds of the lowest-energy local minima in thepointparticlemodel,andenergiesofthecorrespondinglightlybound skyrmions(takenfrom[5],exceptthosemarked∗,whichresultfromnew simulationsconductedwiththesamenumericalscheme).

Name Bonds Particle energy Skyrme interaction energy

2a 2 −0.310 −0.36

3a 3 −0.931 −0.92

4a 6 −1.862 −1.71

5a 8 −2.338 −2.20

5b 8 −2.185 −2.00∗

6a 12 −3.229 −2.85

6b 11 −3.117 −2.87

6c 11 −3.046 −2.79∗

7a 15 −4.057 −3.58∗

7b 14 −3.895 −3.52

8a 18 −4.889 −4.47

8b 18 −4.869 −4.37

8c 18 −4.781 −4.34∗

Fig. 2.Localenergiesminimizersinthepointparticlemodel.Eachballiscentredonapointskyrmionpositionxaandits

colourrepresentstheinternalorientation qa.EachpicturealsodepictstheFCClatticeconfigurationofsize Btowhich

theminimizerbestfits.Thickgreylinesegmentsindicateinterskyrmionbondsnomorethan10%longerthantheFCC bondlength,whilethinmagentalinesegmentsshownearestneighbourbondsinthebestfitlatticeconfiguration.Inmost casesthefitissogoodthatthethinbondsarenotvisible.Theyshowquiteclearlyon5(a),5(b),6(b),6(c),7(b)and8(c) however.(Forinterpretationofthereferencestocolourinthisfigurelegend,thereaderisreferredtothewebversionof thisarticle.)

Ineverycase,theminimizersfoundlook,tothenakedeye,likesubsetsoftheFCClattice.2It isaninterestingproblemtomeasurethispropertyquantitatively.Givenanorientedpointcloud

2 _{All minimizers in this paper can be found at http://www1.maths.leeds.ac.uk/~pmtdgh/}

(X,Q)=(x1,. . . ,xB,q1,. . . ,qB),we wish toidentify theFCC subset of size B which best

approximatesit.Todo this,we considerthe orbitof (X,Q)under thegroupS of similitudes

ofR3,

R3_×(

0,∞)×SU(2)(c, λ, h):x→R(h)(x−c)

λ . (4.1)

Foreachs∈S,wedefined2tobethesquareddistancefroms·XtotheFCClattice,i.e.

d(s)2= B

a=1

min{|xa−n|2 : n∈Z3, n1+n2+n3=0 mod 2}. (4.2)

Now, givenaneighbouringtripleof particlesinX (aparticlex,itsnearest neighbour x and next-nearest neighbour x), we construct a similitude s0 which maps x to 0, x to (1,1,0) andx tothe plane spanned by (1,1,0),(0,1,1). Wethen solve the gradientflow equation of d2:S→R,withs(0)=s0,tofindalocalminimum ofd2 closetos0.Repeatingoverall neighbouringtriples,wekeepthelowestlocalminimumsminofd2found(notethatd2neverhas

aglobalminimumsinces·Xcanbemadearbitrarilycloseto(0,0,0)bytakingλsufficiently large).InthiswayweidentifytheclosestFCCsubsettoX anditsrootmean squaredistance fromX,namelydRMS=

d(smin)2/B.Havingfoundsmin·X,theFCCcolouringrulepredicts

theinternalorientations(q₁,. . . ,q_B )theparticlesshouldhave.Theseshouldbecomparedwith (q1h−_min1 ,. . . ,qBh−_min1),bearinginmindthatorientationsaredefinedonlyuptosign,andthatthe

systemisisospininvariant.Thusweminimize

d_iso2 :SU(2)→R, g→ B

a=1

min{|gqah−_min1 −qa|2,|gqah−_min1 +qa|2} (4.3)

overg∈SU(2)I,againbygradientflow.Thisgivesusameasureoftherootmeansquared

dis-tanceoftheinternalorientationsoftheconfiguration(X,Q)fromthoseimposedbythecolouring

ruleappliedtoitsclosestFCCapproximant,namelyd_RMSiso =

d_iso2 (gmin)/B.Italsoallowsusto

“coarsegrain”theinternalorientations,thatis,mapeachqatotheelementof{±1,±i,±j,±k}

towhichgqah−_min1 isclosest. Weusedthismethodtodeterminetheparticle coloursandFCC

bondsinFig. 2.WewillpresentgraphsofdRMSanddRMSiso inthenextsection.

Inadditiontocomparingenergieswehavealsocomparedinertiatensorsinthepointparticle andlightlyboundSkyrmemodels.Underisorotationsandrotations(g,h)∈SU(2)I ×SU(2)J

inertiatensorstransformas

→

R(g) 0

0 R(h)

R(g)−1 0

0 R(h)−1

.

Table 2

Percentageerrorininertiatensorscalculatedinthepointparticlemodel,ascomparedwiththelightlyboundSkyrme model.

Name 1 2 3 4 5 6b 7a 8a

Error 1.96% 5.96% 1.61% 1.15% 4.65% 9.91% 1.97% 3.20%

= ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝

∗ ∗ ∗ μ1 ν3 ν2

∗ ∗ ∗ 0 μ2 ν1

∗ ∗ ∗ 0 0 μ3

μ1 0 0 λ1 0 0

ν3 μ2 0 0 λ2 0

ν2 ν1 μ3 0 0 λ3

⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠

, (4.4)

where

• λ1,λ2,λ3satisfy|λ1−λ2|≤ |λ2−λ3|≤ |λ1−λ3|;

• ifλ1=λ2 thenμ1,μ2,μ3areeitherallnon-negativeorallnon-positiveandν1,ν2,ν3are eitherallnon-negativeorallnon-positive;and

• ifλ1=λ2thenν3=0,|μ1|>|μ2|,andμ1,μ2,μ3,ν1,ν2areeitherallnon-negativeorall non-positive.

AnyinertiatensorhasamatrixofstandardforminitsSU(2)I×SU(2)J orbit,and,ingeneric

casesthismatrixisunique.Notethatwehavechosennottodefinestandardformasbeingaform inwhichboththeupper-leftandlower-rightblocksof arediagonal,eventhoughsuchaform isarguablysimplerthantheonedescribedabove.Thereasonisthattheupper-leftblockofany inertiatensorobtainedinthepointparticlemodelisproportionaltotheidentity,sodiagonalizing theupperleftblockdoesnotfixtheisorotationsymmetry.Weshallmeasurethedistancebetween inertiatensorsbythedistancebetweentheirstandardforms,usingtheusualEuclideannormon thespaceofrealmatrices,thatis

2_:=

Tr( T ). (4.5)

InTable 2thedistancesbetweeninertiatensorsobtainedinthepointparticleandlightlybound Skyrmemodelsarerecorded.Theerrorsrecordedinthetablearenormalized bydividingthrough by ,where isthelightlyboundSkyrmemodelinertiatensor.Theconfigurationschosen inthiscomparisoncorrespondtoglobalenergyminimainthelightlyboundSkyrmemodel.The valuesofLandMhavebeenchosentooptimize theagreementbetweenthetwomodels,inother words,tominimizethesumoverallchosenconfigurationsofthedistancebetweenthe lightly boundSkyrmeandpointparticleinertiatensors.Theprecisevaluesare

M=93.09, L=54.30.

These arequite closetothe values MH ≈87.49 and LH ≈53.49 obtaineddirectly fromthe

1-skyrmion(3.1).Aswithenergies,agreementofinertiatensorsisgenerallygood(within6%), withoneexceptionatbaryonnumber6.

4.2. Heavier nuclei

particles,andhencethenumberofcandidatelocalminimaoftheenergygrowsrapidly.We ad-dressedthisproblembyseekingonlylocalminimacorrespondingtoFCClatticesubsetswitha largenumberofbonds.Moreprecisely,weusedasinitialconditionsinourrelaxationalgorithm onlylatticesubsetswhosenumberofbondsisatmosttwolessthanthemaximumpossiblefor thegivennumberofparticles.Intheendwefoundthatglobalenergyminimaalwayshadatmost onelessthanthemaximumnumberofbonds,sothisrestrictionseemsreasonable.

Evenwiththissimplification,thenumberofinitialconditions toconsiderislargeanditis difficulttobesurethatenoughsimulationshavebeenruntofindtheglobalenergyminimizer.To solvethisproblemweseparatedourminimizationalgorithmintotwostages:inthefirststage, alistofdistinct latticesubsets isgenerated,andinthesecondstagethesesubsetsarerelaxed as before.Our methodfor telling whether two latticesubsetsare distinct istocompute their energy:if twolatticesubsetshavethesameenergytohighprecisionwe assumethattheyare identicalanddiscardone.Indoingsoweruntheriskthatalatticesubsetwhoseenergyhappens tocoincide withanother is wrongfully discarded. Forexample, the initialFCC subsets used togeneratesolutions6b and6chave exactlythe samespectrumof bonds, andhenceexactly the sameenergy. Onlyafter relaxationaway fromthe FCC latticedo theirenergiesseparate. To mitigateagainst thisdanger we ranextensivesimulations up to16particlesstarting from randomlychosenlatticesubsetssatisfyingthebondnumberconstraint;inallcasesweobtained thesameminimumenergyaswhenwestartedwithalistofdistinctlatticesubsets.

Onedistinctadvantageof ourmethodisthatitmakesiteasytoidentifynotjusttheglobal energy-minimizerbutalsolocalenergyminima. Anotheristhat itallowsonetotellwith rea-sonableconfidencewhensufficientlymanylatticesubsetshavebeensampled.Throughoutthe procedurethenumberofoccurrences ofeachsubsetisrecorded,andwhenallofthesenumbers areaboveafixedminimumonemayassumethatalldistinctlatticesubsetshavebeenfoundand terminatethealgorithm.

Inordertogeneratelatticesubsetstouseasinitialconditionswedevelopedacrystal-growing algorithm.Again,thisalgorithmproceedsintwostages.Inthefirststageaconnectedsubsetof theFCClatticeisgeneratediteratively.Thisschemestartswithalatticesubsetconsistingofa singlepoint.At eachstep ofthe iterationamemberofthe latticesubsetis chosenatrandom andoneof itstwelvenearest neighboursischosenatrandom.If theneighbourisnotalready amemberof the latticesubset, it isappended, otherwiseit isdiscarded. Thiscontinues until thelatticesubsethastherequirednumberofparticles.Inthesecondstageofthealgorithmthe subsetismodifiedsoastoincreasethenumberof bondswhilemaintainingafixednumberof particles.Ateachstepthealgorithmchoosesatrandomonememberofthesubsetandaneighbour ofanothermember.Iftheneighbourisnotalreadyamemberofthesubset,andreplacingthe originalmemberwiththisneighbourincreasesthenumberofbonds,thealgorithmmakesthis replacement;otherwise,nothinghappens.Thiscontinuesfor afixednumberofsteps.Ateach stepofthesecondstagethelatticesubsetisrecorded,sorunningthealgorithmoncegeneratesa largenumberoflatticesubsets.

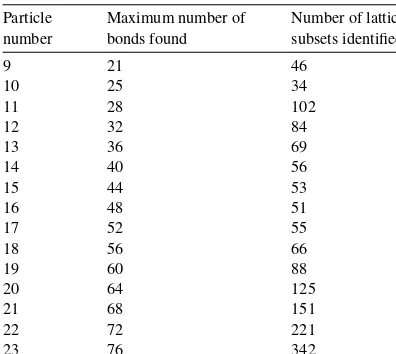
Thecrystal-growingalgorithmwasrunrepeatedlyanddistinctsubsetswithsufficientlymany bondssaveduntilitwasdeemedthatenoughlatticesubsetshadbeensampled,accordingtothe above-defined criteria.The maximumnumberof bondsandthe numberof crystalsidentified satisfyingourcriteriaarerecordedinTable 3.

Table 3

MaximumnumberofbondsinanFCClatticesubsetofgiven size,andthenumberoflatticesubsetsidentifiedbyour algo-rithmwithatmosttwofewerbondsthanthemaximum.

Particle number

Maximumnumberof bondsfound

Numberoflattice subsetsidentified

9 21 46

10 25 34

11 28 102

12 32 84

13 36 69

14 40 56

15 44 53

16 48 51

17 52 55

18 56 66

19 60 88

20 64 125

21 68 151

22 72 221

23 76 342

andhavethemostevendistributionofparticle“colours”(aftercoarsegraining)possible.A no-tableexceptiontoboththeserulesis23a,whichhasonelessbondthanmaximal,andarather unevencolourdistribution(8,5,5,5)butis,nonetheless,thelowestenergyB=23 configuration found.Thisminimizeralsohasunusuallyhighsymmetry,ascanbeseenfromFig. 3,whichalso depictsthehighlysymmetricminimizers10band19b.Oneshouldnote,however,thatthepoint particlemodeldoesnotalwaysfavourhighlysymmetricconfigurations.TheB=13 configura-tion,letuscallit13sym,obtainedbyaugmentingasinglepointbyallitsnearest neighbours, forexample,hasthemaximalnumberofbonds,buthasenergy−8.556,whichismuchhigher thanthe13a.Italsohasaveryunevencolourdistribution:4,4,4,1.SoforB=13,unlikeB=23, the model prefers to sacrifice symmetryin favour of uniform colour distribution. Thesetwo charge13configurationsarealsodepictedinFig. 3.Notethatallparticlesin13aarecontained injusttwoplanesoftheFCClattice,afeatureithasincommonwithallglobalminimizersfor 4≤B≤15.

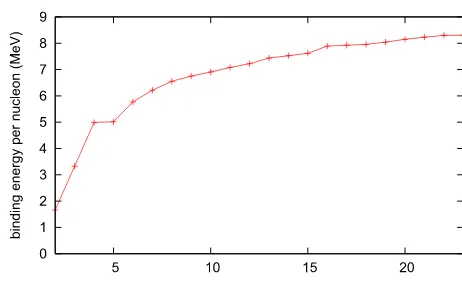
The corresponding predictions for nuclear binding energies per nucleon, defined to be

−Vint/B,areplottedinFig. 4.Here,asin[5],energiesinTable 4havebeenconvertedtoMeV

bymultiplyingwith10.72.Thecurveshowsthatensemblesof4and16particleshaveunusually highbindingenergies,inagreementwithnuclearexperiment,althoughtheseeffectsareless pro-nouncedinthepointparticlemodelthaninexperiment.Theenergyminimizerscorresponding tothesetwopeaksareparticularlyspecial:theybothhavetetrahedralsymmetry.Notethatour bindingenergy curvelacksthe peakseenatbaryonnumber12inthenuclearbindingenergy curve.

Inordertoanalyzetheoverallshapeoftheenergyminimizerswehavecalculatedforeachits secondmomentmatrixMij,definedby

Mij:= N

a=1

(x_ai −x₀i)(xaj−x j

0), x0:= 1 N

N

a=1

Table 4

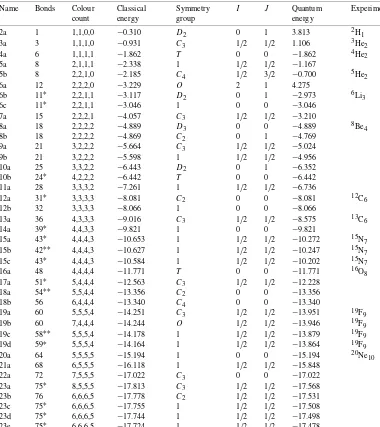
Thelowestenergylocalenergyminimainthepointparticlemodel.Asterisksincolumn2indicatethattheconfiguration hasoneortwofewerbondsthanthemaximumbondnumberfoundforthatparticlenumber.Column3indicatesthe numberofparticlesofeachinternalorientation,aftercoarse-graining.Theclassicalenergyisthepotential Vofeq.(3.4), andthequantumenergyis V+,where isdefinedinsection5.Theexperimentcolumnidentifiesthelightestnucleus forgivenbaryonnumber Bifthisnucleushasthespinandisospinpredicted.

Name Bonds Colour count

Classical energy

Symmetry group

I J Quantum

energy

Experiment

2a 1 1,1,0,0 −0.310 D2 0 1 3.813 2H1

3a 3 1,1,1,0 −0.931 C3 1/2 1/2 1.106 3He2

4a 6 1,1,1,1 −1.862 T 0 0 −1.862 4He2

5a 8 2,1,1,1 −2.338 1 1/2 1/2 −1.167

5b 8 2,2,1,0 −2.185 C4 1/2 3/2 −0.700 5He2

6a 12 2,2,2,0 −3.229 O 2 1 4.275

6b 11∗ 2,2,1,1 −3.117 D2 0 1 −2.973 6Li3

6c 11∗ 2,2,1,1 −3.046 1 0 0 −3.046

7a 15 2,2,2,1 −4.057 C3 1/2 1/2 −3.210

8a 18 2,2,2,2 −4.889 D3 0 0 −4.889 8Be4

8b 18 2,2,2,2 −4.869 C2 0 1 −4.769

9a 21 3,2,2,2 −5.664 C3 1/2 1/2 −5.024

9b 21 3,2,2,2 −5.598 1 1/2 1/2 −4.956

10a 25 3,3,2,2 −6.443 D2 0 1 −6.352

10b 24∗ 4,2,2,2 −6.442 T 0 0 −6.442

11a 28 3,3,3,2 −7.261 1 1/2 1/2 −6.736

12a 31∗ 3,3,3,3 −8.081 C2 0 0 −8.081 12C6

12b 32 3,3,3,3 −8.066 1 0 0 −8.066

13a 36 4,3,3,3 −9.016 C3 1/2 1/2 −8.575 13C6

14a 39∗ 4,4,3,3 −9.821 1 0 0 −9.821

15a 43∗ 4,4,4,3 −10.653 1 1/2 1/2 −10.272 15N7

15b 42∗∗ 4,4,4,3 −10.627 1 1/2 1/2 −10.247 15N7

15c 43∗ 4,4,4,3 −10.584 1 1/2 1/2 −10.202 15N7

16a 48 4,4,4,4 −11.771 T 0 0 −11.771 16O8

17a 51∗ 5,4,4,4 −12.563 C3 1/2 1/2 −12.228

18a 54∗∗ 5,5,4,4 −13.356 C2 0 0 −13.356

18b 56 6,4,4,4 −13.340 C4 0 0 −13.340

19a 60 5,5,5,4 −14.251 C3 1/2 1/2 −13.951 19F9

19b 60 7,4,4,4 −14.244 O 1/2 1/2 −13.946 19F9

19c 58∗∗ 5,5,5,4 −14.178 1 1/2 1/2 −13.879 19F9

19d 59∗ 5,5,5,4 −14.164 1 1/2 1/2 −13.864 19F9

20a 64 5,5,5,5 −15.194 1 0 0 −15.194 20Ne10

21a 68 6,5,5,5 −16.118 1 1/2 1/2 −15.848

22a 72 7,5,5,5 −17.022 C3 0 0 −17.022

23a 75∗ 8,5,5,5 −17.813 C3 1/2 1/2 −17.568

23b 76 6,6,6,5 −17.778 C2 1/2 1/2 −17.531

23c 75∗ 6,6,6,5 −17.755 1 1/2 1/2 −17.508

23d 75∗ 6,6,6,5 −17.744 1 1/2 1/2 −17.498

23e 75∗ 6,6,6,5 −17.724 1 1/2 1/2 −17.478

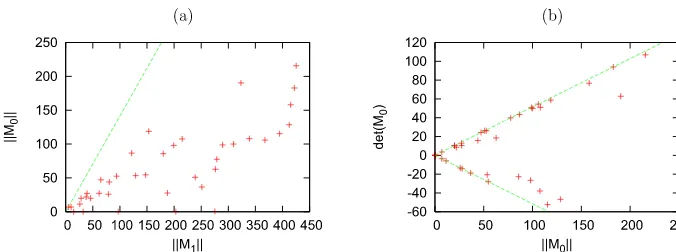
ThismatrixcanbedecomposedM=M1+M0,whereM1=1₃Tr(M)Id3andM0istraceless.The tracepartM1providesameasureofthesizeofthepointcloud{xa}.Ifthecloudisapproximately round,thenMhasnearlyequaleigenvaluesandthetracelesspartM0isclosetozero.Therefore

Fig. 3.Selectedenergyminimizersfor10 ≤B≤23.23aisalargeoctohedronwithatetrahedrongluedtooneface.This unusuallysymmetricconfigurationistheglobalminimizerfor B=23,despitehavinglessthanmaximalbondnumber andratherunevencolourdistribution.Bycontrast,theexceptionallysymmetricconfiguration13symhasmuchhigher energythan13a.Alsodepictedarethelocalminimizers10band19b,alargetetrahedronandoctohedronrespectively.

Fig. 4. Predictions for nuclear binding energies from the point particle model.

defined in(4.5)).Forasymmetricmatrixsuchas M,M2=λ2₁+λ2₂+λ2₃,whereλi areits

eigenvalues.Clearly,M12=3λ 2

whereλ=(λ1+λ2+λ3)/3,andtheeigenvaluesofM0are λi−λ.Hence

M02=(λ1−λ)2+(λ2−λ)2+(λ3−λ)2

=(λ1+λ2+λ3)2−2(λ1λ2+λ2λ3+λ3λ1)−3λ 2

=6λ2−2(λ1λ2+λ2λ3+λ3λ1)≤6λ 2

=2M12 (4.7)

Fig. 5.Graphsshowing(a)theanisotropyofenergyminimizerslistedinTable 4asafunctionoftheirsize,and(b) thetypeofanisotropyoftheseenergyminimizers.ThedashedlinesrepresenttheboundsonM0anddetM0given by(4.7),(4.8).

Thedeterminantdet(M0)measuresthequalitativenatureoftheanisotropy.Letusorderthe eigenvaluesofMsothatλ1≤λ2≤λ3.Ifthepointcloudislongandthinthenλ1≤λ2< λ < λ3, soM0 hastwonegativeeigenvaluesandonepositive,whencedet(M0)>0.Bycontrast,ifthe point cloud is flat andround then λ1< λ < λ2≤λ3, so det(M0)<0. It is useful todefine μi=λi−λ,theeigenvaluesofM0.ByextremizingthefunctiondetM0=μ1μ2μ3onthecircle obtainedbyintersectingthesphereofradiusM0withtheplaneμ1+μ2+μ3=0,onefinds that

− 1

3√6M0

3_≤det(M 0)≤

1 3√6M0

3_{, (4.8)}

withequalitypreciselywhentwooftheeigenvalues(ofM0or,equivalently,M)coincide.Fig. 5 alsodisplaysaplotof√3

det(M0)againstM0fortheminimizerslistedinTable 4.Interestingly, det(M0)isclosetoeitheritsmaximumoritsminimumvalueinthemajorityofcases,indicating thatbothextremesofanisotropyarewell-represented.

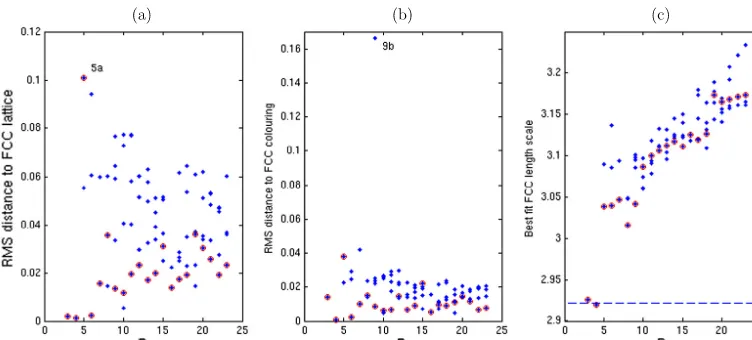
Justasfor 2≤B≤8, wecanmeasurethedistanceofeach localminimumfoundfromits closestFCClatticeapproximant,bothinspaceandininternal(orientation)space,asdefinedin

(4.2)and(4.3).The resultsofthisanalysis arepresented inFig. 6.Withvery fewexceptions theminimizersmatchupverycloselywithFCCsubsets,andtheirinternalorientationsarevery closetotheFCCprediction.Note,however,thattheoptimallatticescalevariesquitesignificantly withB(rightmostgraph),soitisnotagoodapproximationtofixthisatthestart(tomatchthe FCCbondlengthtotheoptimalseparationofasingleskyrmionpair,forexample)andminimize energyonlyoverFCCsubsetsofthatfixedscale.Anyattempttoproceedinthiswayalwaysgets therelativeenergyorderingoflocalminimawrongforseveralvaluesofB.

5. Rigid body quantization

Fig. 6.ComparisonofenergyminimizersofthepointparticlemodelwithsubsetsoftheFCClatticeforbaryonnumber 3≤B≤23.Ineachcaseweshift,scaleandrotatetheconfigurationuntilitmatches,ascloselyaspossible,aconnected subsetofthestandardFCClattice(withintegercoordinates).Plot(a)showstherootmeansquaredistanceoftheparticles ineachtransformedconfigurationfromtheFCClattice,whileplot(b)showstherootmeansquaredistanceoftheir internalorientationsfromthosepredictedbytheFCCcolouringrule.Plot(c)showsthescalefactorused.Ineachcase, datacorrespondingtoglobalenergyminima(i.e.configurationslabelled“a”)arecircledinred.Thedashedlinein(c) markstheoptimallatticescalefor B=2.(Forinterpretationofthereferencestocolourinthisfigurelegend,thereader isreferredtothewebversionofthisarticle.)

solitonshavesymmetrytheyyieldmorenontrivialinformation.Inthepresentsectionwedescribe howtoapplyrigidbodyquantizationandtheFinkelstein–Rubinsteinconstraintsinthepoint par-ticlemodel.Theprocedurereducestoanumericalalgorithmwhichwehaveimplementedand appliedtotheminimapresentedintheprevioussection.

5.1. Finkelstein–Rubinstein constraints

WebeginbyrecallingthedefinitionoftheFinkelstein–Rubinsteinconstraints(readersnot in-terestedintopologicaldetailscouldskipthissubsectionandcontinuereadingatthestartofthe nextsubsection).TheclassicalconfigurationspaceofsolitonswithbaryonnumberBisthespace SBofcontinuousmapsU:R3→SU(2)oftopologicaldegreeB,satisfyingtheboundary

con-ditionU (x)→1 as|x|→ ∞.Thisspaceistopologicallynontrivial:itcontainsnon-contractible loops,sohasanontrivialfundamentalgroup.Infact,π1(SB)=Z2forallB∈Z.SBhasa

univer-salcoveringspaceS˜B togetherwithatwo-to-onemapπS: ˜SB→SB,suchthatallloopsinS˜B

arecontractibleandaloopinSBiscontractibleifandonlyifitcanbeliftedtoaclosedloopin

˜

SB.Thesolitonwavefunctionisafunction: ˜SB→C.TheFinkelstein–Rubinsteinconstraint

on statesthatforeverypairyandyofdistinctpointsinS˜BsuchthatπS(y)=πS(y),

(y)= −(y). (5.1)

AconfigurationofB pointparticlesconsistsof B vectors x1,. . .xB inR3andB elements q1,. . . ,qB ∈SU(2).The energy function disfavoursvectors xa from being too close, so for

practicalpurposeswemaydemandthattheirseparationsaregreaterthansomefixedminimum δ >0.Thereforethenaiveconfigurationspaceforthepointparticlemodelis

˜

R3B_∗:=(

x1, . . .xB)∈(R3)B : |xa−xb|> δwhenevera=b

. (5.3)

ThemaptoSkyrmeconfigurationspaceisgivenbyaso-called“relativized productansatz”

ˆ

F:(x1, . . . ,xB, q1, . . . , qB)→P ⎛ ⎝ 1

N!

σ∈B

B

a=1

U (x;xσ (a), qσ (a)) ⎞

⎠. (5.4)

HereU (x;xa,qa)isdefinedin(3.2),Bisthegroupofpermutationsoftheset{1,. . . ,B},and

P (U )=Tr(U†U )−1/2U.

ApplyingP toasumofproducts ofmatricesinSU(2)yieldsanSU(2)matrix,aslongas the sumofproductsiseverywherenonvanishing.TheargumentofP ineq.(5.4)isnonvanishingif thepositions xaaresufficientlywell-separated,sotherighthandsideisamapR3_→SU(2).

ThemapFˆ: ˜CB→SBineq.(5.4)isnotinjectivesinceflippingthesignofanyorientationqa,

andpermutingtheparticlelabels,leavetheassociatedSkyrmefieldunchanged.Tobeprecise, letB bethe groupofpermutationsof {1,2,. . . ,B}andZ2= {1,−1}.Toeach pair(σ,s)∈ B×(Z2)B,associatethemap

(σ,s): ˜CB→ ˜CB,

(x1, . . . ,xB, q1, . . . , qB)→(xσ (1), . . . , xσ (B), sσ (1)qσ (1), . . . , sσ (B)qσ (B)).

Thisdefines aright actionof B(Z2)B onC˜B byhomeomorphisms,wherethe semi-direct

productcarriesgroupoperation

(σ, s)·(μ, t)=(σ◦μ, (s1tσ−1₍₁₎, . . . , sBtσ−1_(B))).

Thisaction leaves Fˆ invariant, that is, Fˆ ◦(σ,s)= ˆF, so Fˆ descends toa continuousmap F:CB→SBwhere

CB:= ˜CB/B(Z2)B

isthe true pointparticleconfiguration space.Since C˜B is simplyconnectedandthe actionis

free,C˜B is theuniversalcoverof CB andπ1(CB)∼=B(Z2)B.Clearly, Fˆ =F ◦πC where π_C: ˜CB→CBisthecanonicalprojection.

Chooseanypairofpointsx0∈ ˜CB,y0∈ ˜SBsuchthatF (xˆ 0)=πS(y0).Byastandardtheorem oftopology(see[9,pp. 61–62]forexample),Fˆ hasauniquecontinuousliftF˜: ˜CB→ ˜SBwith

˜

F (x0)=y0.Thesituationissummarizedinthefollowingcommutativediagram

˜

CB S˜B

CB SB

˜

F

π_C π_S

F

ˆ

F

. (5.5)

NotethatFisaliftofF.

Anywavefunction: ˜SB→Cdefinesawavefunctionψ=◦ ˜F onC˜B,whichmustsatisfy

Proposition 2. If x,xare two points in C˜B such that πC(x)=πC(x), then

ψ (x)=sgn(σ ) B

a=1

saψ (x),

where (σ,s)∈B(Z2)Bis the unique group element that maps xto x.

Proof. Thisresult follows almostdirectlyfrom two importantresults of Finkelstein and Ru-binstein [4].First,ifx∈ ˜CB,andta∈(Z2)B isthetransformationthatchanges thesignofqa

(only)andαisapathinC˜B fromx to(Id,ta₎(x)thenF ◦π_C◦αisnon-contractible.Second,

ifσ ∈B isatranspositionandβ isapathinC˜B fromx to(σ,1)(x)thenF ◦πC◦αisalso

non-contractible.Thustheconstraint(5.1)impliesthat

ψ ((Id,ta₎(x))= −ψ (x) and ψ (_(σ,1)(x))= −ψ (x).

NowanyelementofB(Z2)Bcanbewrittenasaproductofsignflipsandtranspositions,so

theclaimfollows. 2

5.2. Rigid body quantization

In rigid bodyquantization, motion is restrictedto the rotation–isorotationorbit of afixed minimumx=(x1,. . . ,xB,q1,. . . ,qB)oftheclassicalenergy.Thustheclassicalconfiguration

spaceistakentobeG=SU(2)I×SU(2)J witheach(g,h)∈Gidentifiedwith

(g, h)·(xa, qa)=(R(h)xa, hqag−1)∈ ˜CB.

The wavefunctionψ:G→CisrequiredtosolveaSchrödingerequationH ψˆ =Eψ,where

ˆ

H is(up toaconstant factor)the Laplacian operatoron G associated withthe leftinvariant metric ,theinertiatensorofx.

Inordertomodelanucleusofdefinitespinandisospinoneassumesthatψisaneigenstate of the totalisospin andspin operatorswithisospin I andspin J.Thisis consistentwiththe Schrödinger equationbecause the hamiltonian commutes withtheseoperators. By the Peter– Weyltheorem,anysuchψisafinitesumoffunctionsoftheform

ψ (g, h)= w, ρI(g)⊗ρJ(h)v, v, w∈VI,J :=C2I+1⊗C2J+1,

wherefor ∈ 1₂N,ρ:SU(2)→SU(2+1)denotesthespin-representationof SU(2).For

eachw∈VI,J denotebyV(w)thesubspaceoffunctionswithwfixed.ClearlyV(w)∼=VI,J for

allw=0.Furthermore,Hˆ preservesV(w),anditsactiononeveryV(w=0)isunitarilyequivalent. Hencewemay,withoutlossofgenerality,fixw=0,andrepresentHˆ byalinearoperatorHI,J

onV(w)∼=VI,J.Towritethisoperatordownexplicitly,itisusefultointroducetheusualbasis

forg=su(2)I⊕su(2)J,namely

Ki= −

i

2σi⊕0, Ki+3=0⊕

−i

2σi

, i=1,2,3, (5.6)

withrespecttowhich isasymmetric6×6 realmatrix.Denoteitsentries abandthoseofits

inverse ab.ThenHˆ actsonV(w)∼=VI,J as

HI,J :v→ − ¯ h2

2

ab_ρ∗

whereρ∗_I,J:su(2)I⊕su(2)J→su((2I+1)(2J+1))istheLiealgebrarepresentationassociated

toρI⊗ρJ:

ρ_I,J∗ (Ka)=

ρ_I∗(Ka)⊗Id2J+1 a=1,2,3

Id2I₊1⊗ρ_J∗(Ka) a=4,5,6.

Supposethat(g0,h0)∈SU(2)I×SU(2)Sisasymmetryofx,i.e.thatthereexistsa(σ,s)∈ B(Z2)B suchthat

(R(h0)xa, h0qag₀−1)=(xσ (a), sσ (a)qσ (a)).

ThentheFinkelstein–Rubinsteinconstraintsdescribedintheprevioussectionimplythat

ψ (gg0, hh0)=sgn(σ )

_B

a=1 sa

ψ (g, h) ∀(g, h)∈SU(2)I×SU(2)J.

Thisinturnimpliesthat

ρI(g0)⊗ρJ(h0)v=χ (g0, h0)v, (5.8)

χ (g0, h0):=sgn(σ )

B

a=1

sa. (5.9)

Thuseachelementofthesymmetrygroupofxdeterminesalinearconstraintonv,andv there-foremustbelongtothesubspaceV_I,J(x)⊆C2I+1_⊗C2J+1_{onwhichallof theseconstraintsare} satisfiedsimultaneously.Therefore,tofindthelowestenergyquantizedstateofaconfiguration withisospinI andspinJ oneneedstofindthesmallesteigenvalueoftherestrictionofHI,J

toV_I,J(x).

One important consequence of equation(5.8) is that nucleons have half-integer spin and isospin.Thiscanbededucedusingthetrivialsymmetries(g0,h0)=(1,−1)and(−1,1),which aresymmetriesofanyconfiguration.Bothofthesetransformationsnegatealloftheorientations qa,sothesignappearingontherightofeq.(5.8)is(−1)B.NowρI(−1)equals−Id2I+1ifI is half-integerandId2I+1ifI isinteger,soV_I,J(x)= {0}ifI ishalfintegerandB iseven,orifI is integerandBisodd.Hence,therearenohalfintegerisospinenergyeigenstateswhenBiseven, andnointegerisospinenergyeigenstateswhenBisodd.Similarcommentsapplytospin.

5.3. Two particles

Wenowillustratethequantizationprocedureforthesimpleexample oftwoparticles.After rotationandcentreing,theenergyminimizer2ais

x2a=(x1,x2, q1, q2)=

−√λ

2e1, λ

√

2e1,1,k

, (5.10)