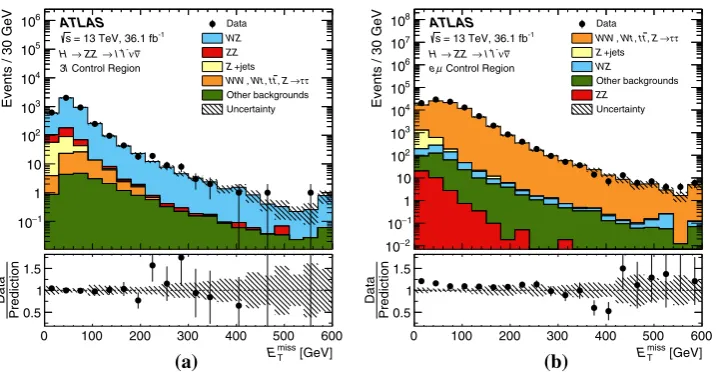
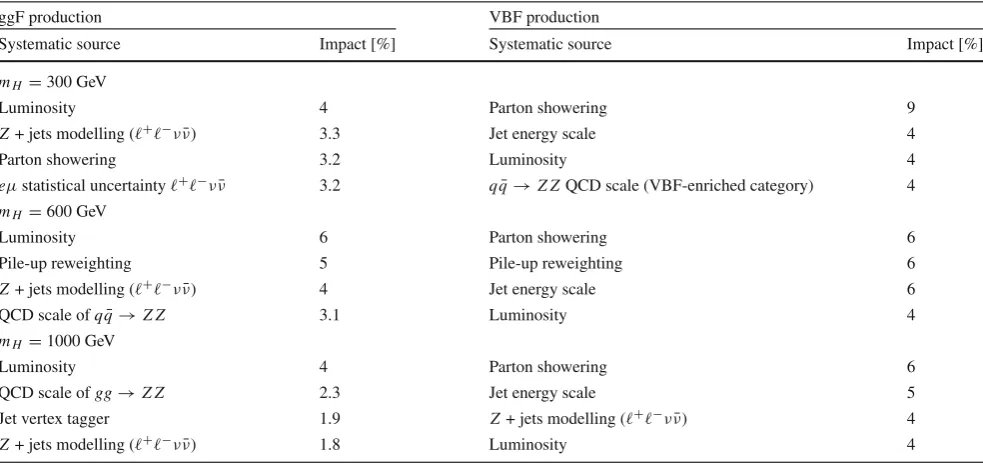
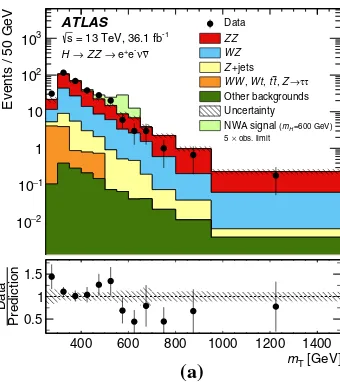
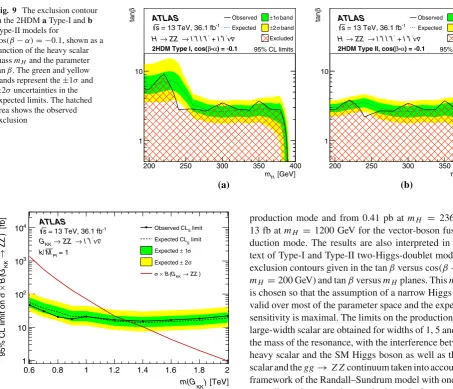
Search for heavy ZZ resonances in the l(+) l(-) l(+) l(-) and l(+) l(-) nu(nu)over-bar final states using proton-proton collisions at root s=13 TeV with the ATLAS detector
Full text
Figure

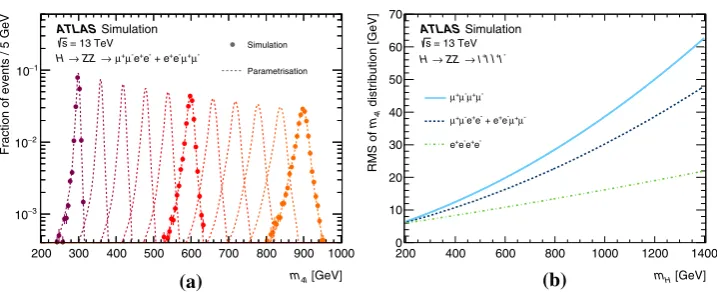


Related documents
critique of religion, which often took the form of a hostile, external attack on the value and.. even actuality of religious phenomena 1 , philosophy of religion has also been quick
On the basis of the Commission's Communication on consumer health and food safety and its Green Paper on food law, the Council held an open debate on what has become the
Recent research has underlined the fact that urban transport and traffic problems are not only related to availability of infrastructure and modes of transport, and
By co-ord1nating stronger IPRs with broader modernisation programmes for assist developing countries in designing an technology development, including human
Le groupe de travail, après discussion, a donc décidé de soumettre à l'Organe permanent l'avis que la question des chantiers mouillés ne pose pas de problème
représentent chaque fois le double de la moyenne régionale.. Obéissant à la tendance générale, la région accuse une baisse sensible du nombre des personnes
Focus on the existing problem in the above method, M. raised local T-Spline skinning method capable of shape preservation [8]. The key points of this method rely in that for
There are some ways to suppress the speckle by reducing the spatial coherence of the laser such as the random laser that can tune the spatial coherence by va- rying the density of