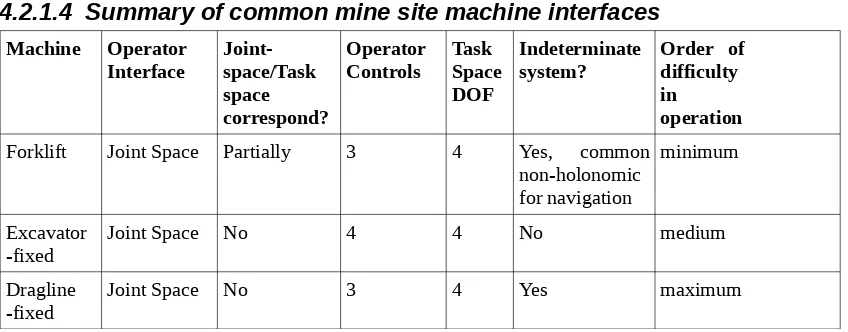
Development of operator interfaces for a heavy maintenance manipulator
Full text
Figure
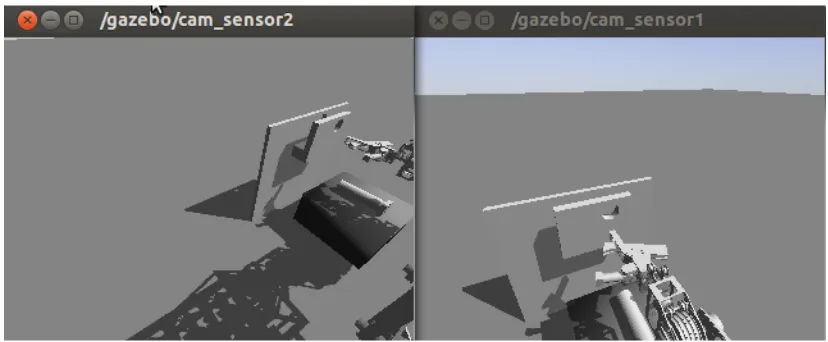

Related documents
While a very small percentage of camps (1%) are weight loss camps that specifically target obese children [17,18] most camps either focus on a specific activity
In this PhD thesis new organic NIR materials (both π-conjugated polymers and small molecules) based on α,β-unsubstituted meso-positioning thienyl BODIPY have been
Significant elevated levels of S100B in older (14 months old) ApoE-PON1 DKO serum was observed compared to age matched control and younger (4 months old) ApoE-PON1 DKO
R1 How will barriers to outdoor play, such as weather conditions, safety concerns for the children, and accessibility to materials, be removed or diminished to encourage teachers
Such a collegiate cul- ture, like honors cultures everywhere, is best achieved by open and trusting relationships of the students with each other and the instructor, discussions
It is clear from Table 4 that HD patients reported significantly lower GHRQoL (both the PCS and MCS) and also higher impact of oral health on quality of life (i.e. poorer OHRQoL)
In this study, it is aimed to develop the Science Education Peer Comparison Scale (SEPCS) in order to measure the comparison of Science Education students'
(G –J) DiI-labeled EVs, isolated from supernatant of control uninfected cells, were stained with anti-gB AF647 antibodies and anti-gH PB antibodies or with their isotype controls..