Investigation of strong earthquake ground motion
Full text
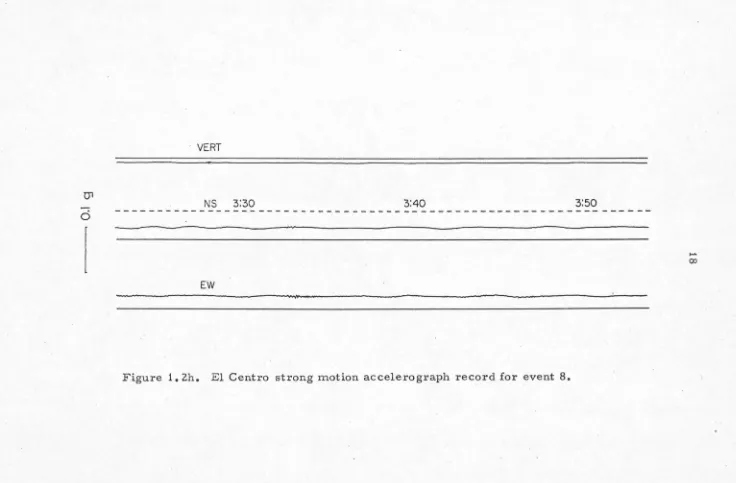
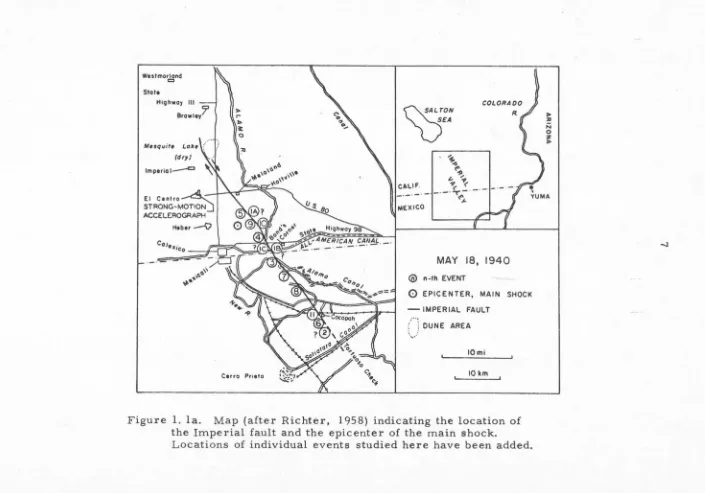
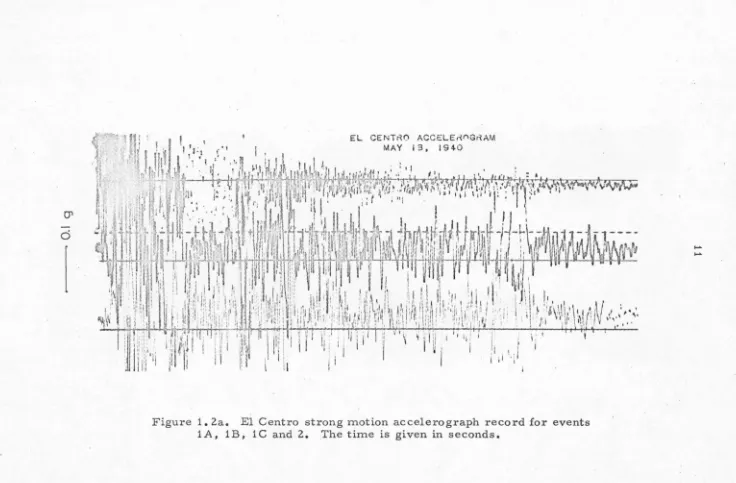
Figure


Related documents
(hereinafter referred to as “the Company”), which comprises the balance sheet as at 31 December 2014, which shows Total Assets of THUF 21,765,529 and retained profit for the year
• The Descrip option takes you to the Project Description menu where you set options that apply to the project in general, such as the title, the unit of time to be
Based on Claim 1, this work proposes to use the common pool method for the overlapping two layers. In case that two sublayers do not completely overlap such as in Fig.5, two layers
The percentage of pulmonary tuberculosis was significantly higher in patients older than 40 years and the percentage of extra-pulmonary TB was significantly higher in patients
The flow of events of a use case includes a main flow, which is the main success scenario and alternative flows, which depict alternate courses of action.. An exception can
This unit seeks to understand the rise, maintenance, and fall of empires by comparing the empire experience in different parts of the world.. We can identify both similarities
Shruthi Dyamanagowdru et.al (April 2015)conducted a study on the treatment of domestic sewage using two species Vetiver and Canna siamensis.Theyhas proved to give
The proposed work gives a algorithm for text to speech conversion. Image to Text and Text to Speech conversion is implemented in this paper using MATLAB. In this paper we can read