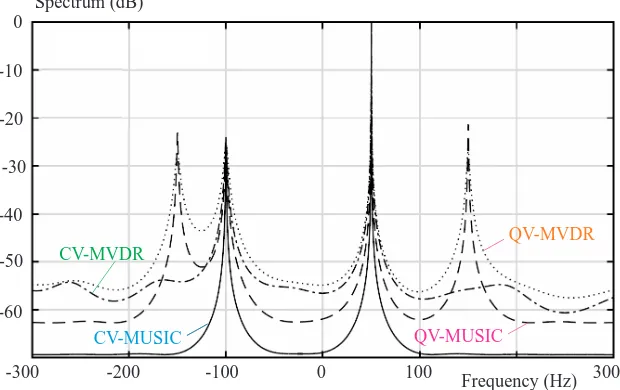
Quaternion-valued single-phase model for three-phase power system

Participants were asked “What should counselors or counseling centers do to make potential Native American clients more comfortable with the idea of getting

Arthrocentesis, Injection of Shoulder, Elbow, Knee & Ankle: Greater Trochanteric Bursa (Excludes Injection of Hip Joint) (ABN# 10) - ACNP, ANP, FMP, & GNP – Allowed

The major findings from the analysed data were that public secondary schools were negatively affected by four main categories of factors: (a) socio-economic factors; (b) the nature

If the vehicle is equipped with the idle bogie, there are active mechanical disk brakes with electro-hydraulic control installed on such bogie with undivided disks located outside

Viewable alarms shall include but not be limited to access control related events such as Door Normal, Door Alarm, Door Trouble, Door Ajar; Card events such as Trace, Not

Following on from the findings of this study and research documented within the Economic and Social Research Council review on ethical issues in visual research [15], we suggest

The hydroxyapatite af fi nity experiment indicated that CUR loaded ALN-HA-C18 micelles exhibited a high af fi nity to bone.. CUR loaded ALN-HA-C18 micelles exhibited much higher

Since Cartesian routing use latitude and longitude pairs to identify the source and the destination addresses of packets, this information is not sufficient to