Strong coupling in a microcavity containing β-carotene
Full text
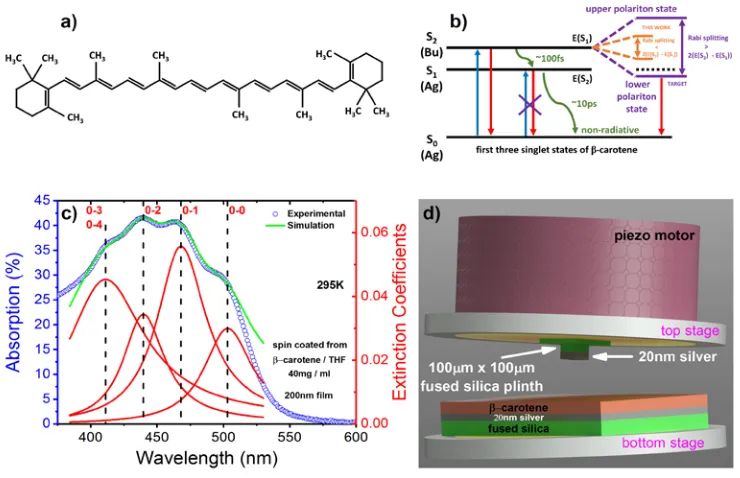
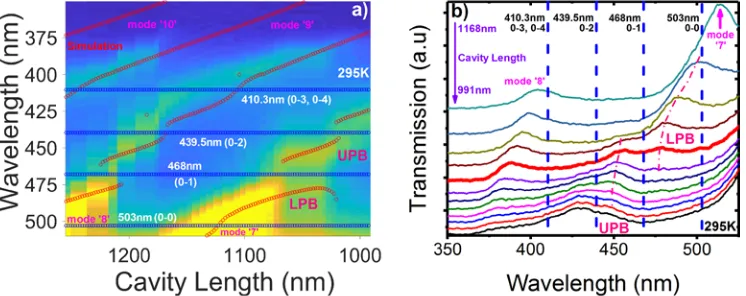
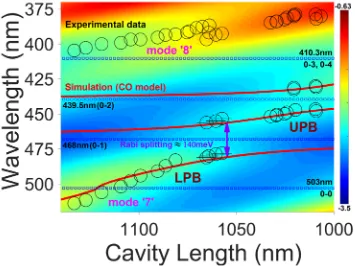
Figure
Related documents
(1) Any person holding a valid hotel certificate shall, on payment of a processing fee of 1,000 rupees, make an application in writing to the Committee for a star rating certificate
The companies Berlin Partner GmbH and ZukunftsAgentur Branden- burg GmbH (Brandenburg Economic Development Board) support with a large range of services, from recruiting
HEIDENHAIN HISTORY For over 100 years, HEIDENHAIN has been a significant force in the precision measurement and motion control industry.. This is the first in a series of columns
This model posits four types of health beliefs that affect an individual’s health behavior, in this case, the decision to seek mental health services: perceived
employment/referral for 1 year. The participant must complete the specified treatment or education program and obtain a return to work release to be eligible for
Using a nationwide database of hospital admissions, we established that diverticulitis patients admitted to hospitals that encounter a low volume of diverticulitis cases have
• Taxpayers subject to the provisions of Title II of the Income Tax Law (ITL) which have declared taxable income of $644,599,005 or more in the immediately preceding tax