Semi-transitive orientations and word-representable graphs
Full text
Figure
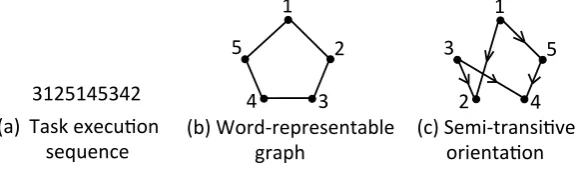
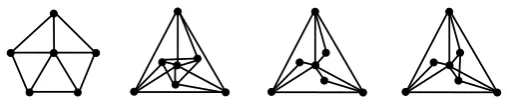
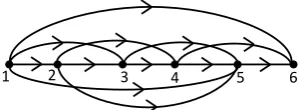
Related documents
The general idea behind the projection is to improve the correlation between the SMI and surface soil moisture at high resolution before applying the downscaling procedure of equation
(Fabaceae: Mimosoideae) in Africa, including new combinations in Vachellia and
Thus, whilst further research is needed to examine the specific influence of these newer, more positive representations on the gendered knowledge and behavior of young children, it
KTP project examples at UoG E-business capability development at TPG Disableaids, Hereford New integrated information systems at Fixing Point, Cheltenham New marketing
Study on the effect of leadership style, reward systems, and working conditions on employee work performance (case study of the state plantation of Merbau Pagar, Indonesia)..
In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Lan- guage Processing (Volume 1:
The Sports Law and Practice course forms part of a wider LLM programme at Leicester De Montfort Law School and for added flexibility, in addition to the Sports Law and