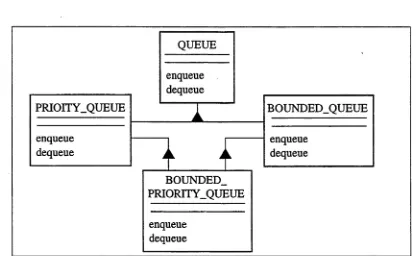
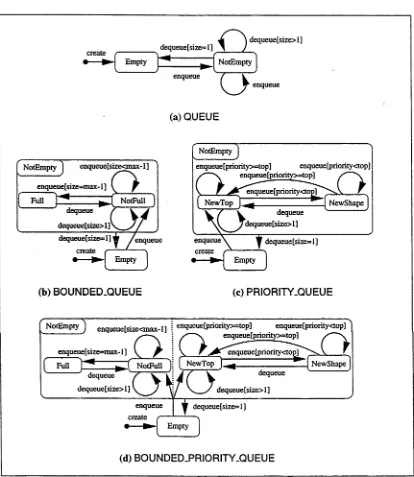
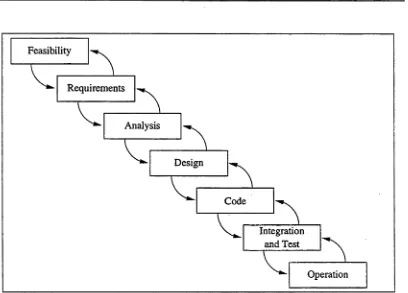
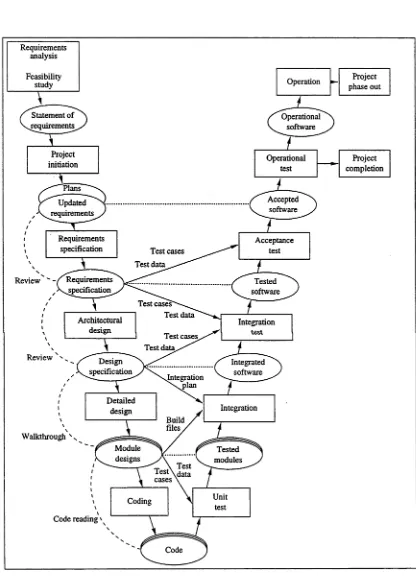
Testing object-oriented software
Full text
Figure
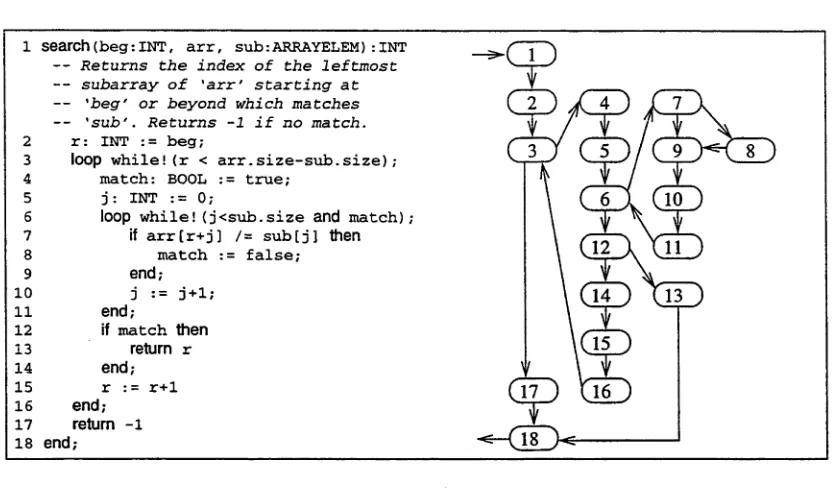



Related documents
Moreover, based on the results, the alkali treated jute fibre reinforcement increases the cement hydration reaction product compared to that of the raw jute reinforced cement
The summary and the comparison of the design concepts (non-nuclear), the nuclear safety standards and specifications for structural steelwork and pipe supports show, that the change
based on the Pediatric Sleep Questionnaire (Chervin et al, 2000). •
This debt is the ransom price our perfect innocent substitute – Jesus Christ – had to pay to free us from bondage to sin, lawlessness, guilt, eternal punishment
The estimated values of both the peak discharge and time to peak were applied to the dimensionless hydrograph ratios in accordance to SCS and the points for the unit hydrograph
Not only the annual average rainfall is declining in the region of Sine Saloun, also the distribution per month of the annual total rainfall is varying from one year
The rise in the demand for human capital in the second phase of industrialization brought about a significant reduction in fertility rates and population growth in various
Two Gaultheria antipoda fruits before and after wētā feeding: (left) fruit part-eaten by a single ground wētā (Hemiandrus ‘evansae’) in a single night; (right) an intact