James Taylor
A thesis submitted for the degree of
Doctor of Philosophy
The Australian National University
This thesis comprises five original research papers, and an introduction. This thesis is within the 100,000 word limit.
I certify that all research chapters are co-authored with José Rodrigues-Neto. The modeling work was split evenly between the authors. The research topic, selection of methodology, connection with the literature, and production and presentation of slides were entirely my own work.
All research papers are manuscripts in preparation for submission.
James Taylor 2 June 2019
I am eternally grateful to José Rodrigues-Neto - the chair of my supervisory panel at The Australian National University - for his exemplary supervision. I thank Simon Grant and Idione Meneghel - the other members of my supervisory panel - for their helpful advice and suggestions.
Those who have given helpful suggestions are too numerous to all recount here, but I would specifically like to thank Aurélien Baillon, Ben Chen, Simona Fabrizi, Lu-ciana Fiorini, John Hillas, Jeffrey Kline, Ruitian Lang, Steffen Lippert, George Mailath, Rogério Mazali, Andrew McLennan, Matthew Ryan, Larry Samuelson, Jack Stecher, and Toru Suzuki for their helpful advice and suggestions on some or all chapters of this thesis. In addition, I am grateful for the comments of three anonymous examiners.
I thank my family, particularly my parents Colleen and Alan, for their unwavering support and exceeding patience over these many years. I also thank my comrades in the PhD trenches - Ben Chen, Max Halupka, Dana Hanna, Miles Keighley, Jessie Moritz, and Emma Vines - for sharing this experience.
Finally, I thank Emma Vines for helping with English editing. Any remaining errors remain, as always, my own responsibility.
Economic analysis containing agents with incomplete information is common in many fields of economics, most notably Game Theory and Decision Theory. In these fields, information structures are typically represented by a state space of outcome-relevant variables, and each agent is endowed with a partition of the state space representing their information about the state of the world. This modeling implicitly assumes a great deal of logical sophistication on the part of agents in the model. For instance, agents can undertake introspection, and can never be mistaken.
This thesis considers some effects of weakening various rationality assumptions on individuals’ information processing capabilities. We allow agents to have much more general forms of information structures in which agents may be mistaken, or potentially not understandmodus ponens. These information structures are formalized by the knowledge operator, a function which takes each event into the set of states where the agent knows that the event has occurred.
One consequence of this relaxation of assumptions is that the classical Aumann [1976] and Lewis [1969] definitions of common knowledge lose a range of desirable properties. A new definition of common knowledge is developed which reduces to the classical definitions when agents have sufficiently strong information processing ca-pabilities, and retains many desirable properties even when agents lack these abilities. Information aggregation more generally is formalized, and a language for discussing knowledge aggregation is developed.
Knowledge operators are used to develop a framework for the study of imprecise probabilities, the Behavioral Imprecise Probability. This new framework uses a stan-dard probability function over the state space to capture Knightian risk, while the knowledge operator captures Knightian uncertainty, or ambiguity. Behavioral Impre-cise Probability Models are systematically compared to existing frameworks of impre-cise probability including the Multiple Prior Model of Gilboa and Schmeidler [1989], and totally monotone capacities, as in Dempster [1967], Shafer [1976], and Gilboa and Schmeidler [1994].
Acknowledgments v
Abstract vii
1 Introduction 1
1.1 Thesis Outline . . . 3
2 Knowledge Aggregators 7 2.1 Introduction . . . 8
2.2 Knowledge Aggregation . . . 11
2.2.1 General Knowledge Aggregation . . . 12
2.2.2 Classical Knowledge Aggregators . . . 12
2.3 Core Properties of Knowledge Aggregators . . . 15
2.3.1 Anonymity, Associativity, and Identity . . . 15
2.3.2 Relative Informativeness . . . 20
2.4 Logic Properties of Knowledge Aggregators . . . 25
2.4.1 Partitions and Correspondences . . . 25
2.4.2 Modal Logic’s S5 Axioms . . . 29
2.4.3 Monotonicity . . . 32
2.4.4 Cognitive Dissonance . . . 33
2.5 Knowledge Modeling through Collections of Events . . . 34
2.A Proofs . . . 39
3 Common Knowledge for Rational and Behavioral Agents 65 3.1 Introduction . . . 66
3.2 Kripke Rationality and Operator Knowledge Models . . . 69
3.3 Classical Common Knowledge Operators . . . 70
3.3.1 Properties of the Classical Operators . . . 71
3.3.2 Breakdown of the Classical Operators . . . 73
3.4 Behavioral Common Knowledge . . . 74
3.4.1 Defining Behavioral Common Knowledge . . . 74
3.4.2 Properties of Behavioral Common Knowledge . . . 78
3.4.3 Behavioral Common Knowledge and the S5 Axioms . . . 80
3.5 Alternative Ideas of Behavioral Common Knowledge . . . 81
3.6 Interpreting Behavioral Knowledge . . . 85
3.7 Conclusion . . . 87
3.A Proofs . . . 88
4 Imprecise Probabilities under General Information Structures 103 4.1 Introduction . . . 104
4.2 Behavioral Imprecise Probabilities . . . 106
4.2.1 Existence and Uniqueness . . . 110
4.2.2 Rationality Assumptions . . . 113
4.3 Relation to other Imprecise Probability Models . . . 118
4.3.1 Multiple Prior Models . . . 118
4.3.2 Dempster-Shafer Models . . . 121
4.3.3 Monotonicity and Dempster-Shafer . . . 128
4.4 Applications . . . 132
4.4.1 Ellsberg Paradox . . . 133
4.4.2 Sorites Paradox . . . 135
4.4.3 Cautious Agents . . . 137
4.4.4 Tversky and Kahneman Behavioral Agents . . . 138
4.5 Conclusion . . . 140
4.A Proofs . . . 141
5 Cycles and Common Priors without Full Support 157 5.1 Introduction . . . 158
5.2 Model Setup . . . 160
5.3 Common Priors without Full Support . . . 162
5.4 Connectedness . . . 168
6 Atomic Cycles and Common Prior Existence 175
6.1 Introduction . . . 176
6.2 Model Setup . . . 177
6.3 Atomic Cycles and the Common Prior . . . 179
6.4 Relative Informativeness . . . 185
6.5 Conclusion . . . 190
Introduction
Most economic analysis assumes a great deal of logical sophistication on the part of the agents in the model. Information structures are typically assumed to be represented by a partition of the state space. However, such a representation requires that agents are capable of substantial logical sophistication. For example, an agent with a partitional information structure can undertake both positive and negative introspection, and can never be mistaken, among other logical processing capabilities. In the first part of this thesis, we break away from these assumptions on the processing capabilities of the agents, and allow agents with arbitrarily poor information structures. There are two main reasons we would like to drop these assumptions. The first is the argument from behavioral economics. As a field, behavioral economics has becoming increasingly im-portant within the economics disciple, now having Nobel Prizes for work in behavioral economics held by Kahneman (2002), Shiller (2013), and most recently Thaler (2017). Perhaps the key message from the field of behavioral economics is that agents do not have perfect information processing abilities, and that this deviation from rationality is not random, but can be systematic. For this reason, we would like our models to allow for agents which can exhibit behavioral qualities. The second argument for weaken-ing the rationality assumptions is a simple matter of intellectual curiosity. We would like to know what results are lost when agents are permitted to have less than ideal knowledge structures, and what results are robust to such changes.
Once the various rationality assumptions have been removed, it is no longer suffi-cient to use a partitional, or even signal-based, model of knowledge. In the first part of this thesis, we use knowledge operators to represent the information structure of an agent. This method can be rooted in Modal Logic, however we only use simple set-theoretic constructions when discussing knowledge. This is because knowledge operators provide us with sufficient flexibility for our discussion, and because they are
of much greater familiarity to the reader.
Throughout the first part of the thesis, we will be using the term ‘knowledge’, even when the agent may have information structures which are far from being consistent with full rationality. In particular, the agent could be mistaken in their knowledge. In this work, knowledge is really what the agent claims to be certain of, rather than the classical definition as justified true belief. If this is of great concern, we are happy for the reader to substitute the word ‘belief’ or ‘certainty’ instead of knowledge. We use the term knowledge because, when an agent is making decisions, agents act ‘as if’ they actually know what they claim to know.
The second part of this thesis retuns to the usual partitional model of knowledge, and focuses on the common prior assumption, and related Harsanyi Consistency Prob-lem (Harsanyi [1967, 1968a,b]). The common prior assumption is a standard assump-tion in most economic analysis. This assumpassump-tion posits that all players have the same underlying probability assessment of the world, or priors, and differ in their even-tual assessments, or posteriors, only due to differences in information. While this assumption is widely used in almost all applications, it has long been known to cause significant problems in the form of No Trade Theorems. The seminal result of Aumann [1976] shows that when players have common priors, they cannot agree to disagree. Work by Rubinstein [1975], Kreps [1977], Milgrom and Stokey [1982], Geanakoplos and Polemarchakis [1982] and others reframe this result to say that, under common priors, players cannot have incentive to trade purely based on differences of infor-mation. The Harsanyi Consistence Problem asks how restrictive the common prior assumption actually is as an assumption. That is, what restrictions are actually being made on the posteriors by the common prior assumption. Samet [1998a,b] provides solutions to this problem using separation of convex sets, and iterated expectations. Rodrigues-Neto [2009, 2012] provides an alternative solution using a graph called the meet-join diagram. Chapter 5 uses the machinery of Rodrigues-Neto [2009] to provide a solution to the Harsanyi Consistency Problem when players priors and posteriors do not necessarily have full support. Chapter 6 refines the main result of Rodrigues-Neto [2009] to produce a tractable algorithm for checking for common prior consistency.
limited information is studied primarily in game theory and decision theory. Game theory has known applications in evolutionary biology, marketing, political science and computer science. Games with limited information are of significant interest in these areas. More recently, limited information is of use in computer science when working on problems associated with artificial intelligence. The modeling of artificial intelligence which mirrors the information processing capacity of humans requires that even very logical artificial intelligence programs need to be able to properly model the poor information processing capacities of behavioral humans.
1.1
Thesis Outline
This thesis is divided into two main lines of research. Chapters 2, 3, and 4 are concerned primarily with dropping a variety of rationality assumptions on agent’s information processing abilities. This part of the thesis assumes agents may not have partitional information structures, and investigates the consequences of dropping this assumption. Chapter 2 establishes a language for discussing knowledge aggregation in a general context. Chapter 3 constructs a novel definition of Common Knowledge which has many desirable properties even when the agents in the model may have undesirable information structures. Chapter 4 uses generalized knowledge structures to create a new framework for the study of imprecise probability.
Chapters 5 and 6 use simple graph theory to approach the Harsanyi Consistency Problem (Harsanyi [1967, 1968a,b]). Chapter 5 extends the main results of Rodrigues-Neto [2009] to solve the Harsanyi Consistency Problem in cases where priors and posteriors are allowed to have less than full support. Chapter 6 refines the results of Rodrigues-Neto [2009, 2012], producing a solution to the Harsanyi Consistency Problem using only relatively short cycles of a graph called the meet-join diagram.
knowledge’, and what is ‘distributed knowledge’. Most of these are standard, and distributed knowledge asks what can be determined by cooperating agents under di-rect communication. Various regularity and preservation properties of aggregators in general, and these examples in particular, are developed and investigated. Notably, the relationship between aggregators and the Kripke S5 axioms are discussed in depth.
Chapter 3 approaches the issue of constructing the appropriate definition of com-mon knowledge when agents have arbitrary information structures. Classically, Au-mann [1976] states that an event is common knowledge if “both know it, 1 knows that 2 knows it, 2 knows that 1 knows it, 1 knows that 2 knows that 1 knows it, and so on”. This definition of common knowledge works very well when agents have sufficiently well-behaved information structures. However, if agents do not have nice information structures, then the Aumann definition of common knowledge has some undesirable properties. Notably it is possible for an event to be common knowledge, but for no agent to know that the event is common knowledge. The same issue exists for the classical Lewis [1969] definition of common knowledge. This chapter constructs a new definition of Behavioral Common Knowledge which matches the classical defini-tions when agents are well-behaved, but still retains desirable properties when agents have arbitrary information structures. A recursive method based on a formal idea of ‘knowledge questions’ is used to build this new definition. Interactions between the new concept of common knowledge and the Kripke S5 axioms are explored. Other alternative ideas of common knowledge for behavioral agents are considered, with shortcomings shown for each alternative.
is the probability you think the event is possible. This model allows for a wide range of behavior, most notably agents can lack monotonicity. This means the Behavioral Imprecise Probability model is not necessarily a capacity. Therefore, the results of Tversky and Kahneman [1983], where agents display non-monotonic probabilities, can be analyzed. The Behavioral Imprecise Probability model is systematically compared to the Common Prior and Totally Monotone Capacity models, and the interaction of Behavioral Imprecise Probability with various rationality assumptions is explored. A range of applications are discussed.
Chapter 5 analyzes the problem of common prior existence when the priors and posteriors for the players may not have full support. This chapter returns to the tra-ditional, partitional model of knowledge. The departure from existing literature is to allow priors and posteriors without full support. Morris [1994], Samet [1998a,b], and Rodrigues-Neto [2009] provide solutions to the common prior existence problem, but all assume that priors and posteriors have full support. This chapter provides a natural extension to Rodrigues-Neto [2009], using the simple graph constructions of Rodrigues-Neto [2009], but where priors may not have full support. Rodrigues-Neto [2009] finds that a common prior exists if and only if all cycle equations of the meet-join diagram are satisfied. When moving away from full support common priors, we can only say that if all cycle equations are satisfied, then there exists a common prior. The role of connectedness is also discussed in detail, and is of particular interest for the uniqueness a common prior, should it exist.
Knowledge Aggregators
Given a group of agents with heterogeneous information, there are many po-tential forms for combining agents’ information. This chapter introduces some language for investigating different methods of aggregating information within groups, where the knowledge of each agent or group of agents takes the general op-erator form. The opop-erator form allows for the modeling of agents who are less than perfectly rational in their information processing. Various specific aggregation formulations are considered in detail, including what ‘somebody knows’, what ‘everybody knows’, common knowledge, and distributed knowledge. Distributed knowledge is what can be determined by cooperating agents, given their infor-mation, under direct communication. Regularity and preservation properties of aggregators are investigated and applied to the specific aggregators listed.
2.1
Introduction
The problem of combining attributes of multiple agents into a single attribute has a long history. The Condorcet Paradox, identified by Condorcet [1785], highlights the issues surrounding the aggregation of individuals’ preferences. While each agent may have well-defined preferences, the group as a whole may end up with non-transitive preferences when pairwise preferences are elicited though majority voting. Demand ag-gregation, and the existence of a representative consumer, face similar issues. Samuel-son argued in 1956 that“Community indifference curves of the type needed for the derivation of community demand do not exist” (Samuelson [1956]). Gorman [1961] gave explicit circumstances under which such demand aggregation is possible.
Similar problems arise in the context of incomplete information when attempting to aggregate individuals’ knowledge structures. When knowledge partitions, as in Aumann [1976], are taken as the primitives of the model, certain natural aggregations do not lead to group knowledge partitions. For example, suppose there are three possible outcomes to some process, say High, Medium, or Low. Ann knows if the outcome will be High, while Bob knows if it will be Low. The modeler can ask when does ‘somebody know’ the outcome. Clearly, somebody knows if the outcome will be High, or if it will be Low, but no-one knows if it will be Medium. The information structure necessary to convey what ‘somebody knows’ does not admit a representation in the usual partition framework of knowledge. This problem remains even if the set of available information structures is expanded to allow correspondence, or signal-based, knowledge. The correspondence, or signal, approach to information representation allows each state of the world to be associated with the set of states the agent considers possible at that state. In this example, when the state is Medium, Ann rules out High, while Bob rules out Low. Thus, somebody rules out High and somebody rules out Low, but no-one rules out both High and Low. The information structure necessary to convey what ‘somebody knows’ does not even admit a representation in the correspondence framework of knowledge.
This chapter introduces the concept of knowledge aggregators and proposes some methods of classifying these structures. The idea of an aggregator is to generate a single new knowledge operator based on the operators of a group of agents. A knowl-edge aggregator takes the operators from multiple agents and combines them into a new knowledge operator which describes the ‘group’ knowledge, for varying ideas of what ‘group’ knowledge might mean. Aggregators which are investigated in some detail include what ‘somebody knows’, what ‘everybody knows’, what is ‘common knowledge’, and what is ‘distributed knowledge’.
Various properties of aggregators are proposed and investigated. Standard proper-ties arising from viewing aggregators as functions of multiple inputs, such as anonymity, associativity, label neutrality, and identity, are considered. An aggregator is anonymous if changing the label on the agents does not change the aggregation, while the aggrega-tor is label neutral if changing the label on the states does not change the aggregation. An aggregator is an identity if, when all agents have the same knowledge operator, the aggregation has this operator as well.
Properties related to relative informativeness are also developed. Aggregators are classified as positive or negative aggregators. Positive aggregators increase the amount of information known following the aggregation and can be associated with cooper-ative situations. Negcooper-ative aggregators restrict the amount of information known fol-lowing the aggregation, and are best associated with competitive situations. A simple criterion for identifying these properties is given.
Knowledge operators are often assumed in the literature to have certain regularity properties which can be interpreted as rationality assumptions, notably the various assumptions contained in Kripke’s S5 system for Modal Logic.1 Aggregators are said
to preserve these rationality assumptions, or logic properties, if, whenever every agent has some aspect of rationality, then the aggregated information also has that aspect. Strong rationality assumptions, such as the partition assumption of Aumann [1976] are considered, as well as a range of weaker assumptions. Generally speaking, the example aggregators considered tend to have fairly weak preservation properties.
An equivalent formulation for knowledge operators based on ‘collections of known events’ is introduced. In this formulation each state of the world is associated with
the collection of events which an agent knows has occurred. Some results allow more direct proof when thought of in terms of these collections of known events, rather than using the knowledge operators directly.
An equivalent formulation of knowledge operators can be given in terms of possi-bility operators. Using possipossi-bility operators, an event is considered possible if an agent is not certain that the event has not occurred. This chapter does not use possibility operators, as all work can be done purely in terms of knowledge operators, and the formulations are exactly equivalent.
These aggregation properties can also be viewed as helpful tools in the study of behavioral economics. Firstly, the weaker conditions imposed by knowledge opera-tors, compared to partitions or correspondences, allow the existence of agents who are not rational in terms of information processing. The modeling presented allows the existence of agents who process information in a ‘behavioral’ manner. Secondly, be-cause we can view an agent as being made of multiple competing selves, this modeling allows us to aggregate the information of each ‘self’ into a single entity. This justifies emergent behavior in which each ‘self’ can be fully rational, though the combined entity may not be.
Many other fields of study also investigate rationality and information aggregation, principally philosophy and computer science. The S5 logic system used in Kripke semantics is taken as an important case study in this work. In this chapter, these ideas are able to be explored by appealing purely to set theory, allowing a wider audience in the economics field than most of the work in Modal Logic.
Information and knowledge concerns are very important in economics and game theory. From auctions to contract theory, the precise modeling of information is of paramount importance for the understanding of incentives and preferred strategies of strategic agents. Information concerns are critically relevant even in the absence of strategic considerations. Much has been written about decision making under uncer-tainty.2
Aumann [1976] introduces the partitional approach to model knowledge and com-mon knowledge. Geanakoplos [1989a, 1992], and Brandenburger et al. [1992] study
2Initial work in this field includes Von Neumann and Morgenstern [1947], Savage [1954], and
the correspondence model. Samuelson [2004] reviews how economists have modeled knowledge and information. Unawareness is treated in great detail in Dekel et al. [1998], Fagin and Halpern [1987], and Heifetz et al. [2006].
Section 2.2 defines knowledge operators and aggregators, and introduces example aggregators to be investigated in subsequent sections. Section 2.3 considers properties of aggregators derived from aggregators being functions of multiple inputs, as well as those properties related to the relative informativeness of the agents’ knowledge operators. Section 2.4 considers some rationality assumptions that can be made on the set of knowledge operators, and how these restrictions interact with knowledge aggre-gators. Section 2.5 gives an alternate formulation of knowledge operators. Appendix 2.A contains all proofs.
2.2
Knowledge Aggregation
A state space is a non-empty finite setΩof outcome-relevant states. Let2Ω be the set of
all subsets ofΩ. There is a non-empty, finite list (ordered set)Jof agents, with a typical agent being denotedj. Knowledge for each agentj ∈J is represented by a knowledge operatorKj : 2Ω → 2Ω. The usual interpretation is that, for each eventE ∈ 2Ω, the
subsetKjEcontains the states at which agentj knows that eventEhas occurred. That
is, agentj knows the eventE has occurred at stateωprecisely whenω ∈KjE. LetK
be the set of all possible knowledge operators,K = {K : 2Ω → 2Ω}. Different agents
may have the same knowledge operators, while some knowledge operators may not be held by any agents.
Definition 2.1. A tuple(Ω, J,{Kj}j∈J)is a knowledge model, whereΩis a state space,J is a
finite list of agents, and eachKj is a functionKj : 2Ω → 2Ω which is the knowledge operator
for agentj ∈J.
Knowledge operators are not restricted in any way. For example, it is entirely possi-ble that an agent claims to know things which are not true. That is,ω ∈KjE, butω /∈E.
2.2.1
General Knowledge Aggregation
A knowledge aggregator is a function that takes as input the knowledge operators of multiple agents, and produces a single new knowledge operator which represents the ‘group knowledge’ in some sense. The particular aggregator which may be of use to a modeler will depend on the problem at hand. In many game-theoretic situations, the aggregation of common knowledge is of great importance. If constructing a team project, where it is only important that somebody knows the relevant information, then a ‘somebody knows’ aggregation will be of greatest interest. Any function which takes in the information from multiple agents and constructs a new knowledge operator is a knowledge aggregator.
We are not concerned in this work with the method by which information is trans-ferred between agents, algorithms which generate the group knowledge, or informa-tion revelainforma-tion mechanisms. Our concern is exclusively with the final form and prop-erties of group knowledge, or knowledge aggregation, which is obtained.
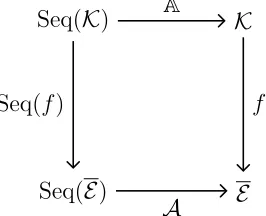
Definition 2.2. LetΩbe a finite state space, andK={K : 2Ω →2Ω}be the set of functions
from2Ωto2Ω. LetSeq(K)be the set of all finite sequences of elements ofK.
A knowledge aggregatorAis a function:
A: Seq(K)→ K
The sequence of knowledge operators represents the knowledge operators for some collection of agents. LetJ = (1,2, . . . ,|J|)be a finite list of agents and(K1, . . . , K|J|)be the sequence of knowledge operators associated withJ. To simplify notation we write
AJ to mean A(K1, . . . , K|J|). It must be emphasized that where A is an aggregator, a function Seq(K) → K, the symbol AJ refers to a knowledge operator, a function
2Ω →2Ω.
Definition 2.3. Let (Ω, J,{Kj}
j∈J) be a knowledge model, and A : Seq(K) → K. The
knowledge aggregationAJ : 2Ω →2Ω is the knowledge operator given by
AJE =A(K1, . . . , K|J|)E, for allE ∈2Ω
2.2.2
Classical Knowledge Aggregators
aggregator, denoted∧, somebody knows aggregatorg, and the distributed knowledge aggregator, denoted∨. The intuitive idea of ‘somebody knows’ and ‘everybody knows’ are fairly self-explanatory. The common knowledge is well-studied in the economics literature, and is the concept that everybody knows, and everybody knows that ev-erybody knows, and so on ad infinitum. Common Knowledge is discussed in much greater detail in Chapter 3. Distributed knowledge is more familiar in the Modal Logic literature, and describes what agents can know if they work together by directly and completely sharing information.
We will usually be interested in how these knowledge aggregators behave on a given knowledge model(Ω, J,{Kj}
j∈J). Often we will write the corresponding
opera-tors in the simplified forms:fJ,∧J,
gJ and∨J.
Definition 2.4. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. Define the everybody knows aggregator f : Seq(K) → K pointwise at each sequence
(K1, . . . , Kn)∈Seq(K)and eventE ∈2Ω, by
f(K1, . . . , Kn)E =
n
\
i=1
KiE
For a knowledge model(Ω, J,{Kj}
j∈J), the everybody knows aggregationfJ : 2Ω →2Ωis
fJE = \
j∈J
KjE
Each stateω belongs tofJE when, atω, all agentsj ∈J know eventE.
In order to define common knowledge, let(K)(s) denote the operatorK applieds
times for anys ∈N={1,2,3, . . . ,}. Iterated application of this operator is possible as it has the same domain and codomain, namely the power set2Ω.
Definition 2.5. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. Define the common knowledge aggregator ∧ : Seq(K) → K pointwise at each sequence
(K1, . . . , Kn)∈Seq(K)and eventE ∈2Ω, by
∧(K1, . . . , Kn)E =
∞
\
s=1
f(K1, . . . , Kn)(s)E
For a knowledge model(Ω, J,{Kj}
j∈J), the common knowledge aggregation∧J : 2Ω→2Ω is
∧JE =
∞
\
s=1
EventEis common knowledge atωif everybody knowsE, and everybody knows that everybody knowsE, and so on, ad infinitum.
This is the definition of common knowledge as in, for example, Bacharach [1985]. Alternative definitions for common knowledge are often used, as in, for example, Au-mann [1976]. Both are generally equally useful definitions of common knowledge. For brevity, this chapter restricts attention to the Bacharach version of common knowledge presented in Definition 2.5.3 Chapter 3 explores the distinction between the Bacharach
and Aumann definitions. In Chapter 3, the definition given here is referred to as ‘re-peated everybody knows’, to distinguish it from the Aumann definition which is based around sequences of players. This distinction is formalized in Definitions 3.3 and 3.4.
Definition 2.6. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. Define the somebody knows aggregator g : Seq(K) → K pointwise at each sequence
(K1, . . . , Kn)∈Seq(K)and eventE ∈2Ω, by
g(K1, . . . , Kn)E =
n
[
i=1
KiE
For a knowledge model(Ω, J,{Kj}j∈J), the somebody knows aggregationgJ : 2Ω →2Ωis
gJE = [
j∈J
KjE
Each stateω belongs togJE when, atω, at least one agentj ∈J knows eventE.
Next we focus on distributed knowledge. Under distributed knowledge, the knowl-edge aggregation knows event E at state ω if, working collectively, the agents can determine that each state not inEhas not occurred. It is an elimination process.
For an eventE ∈2Ω, the complement ofEis denoted¬E = Ω\E. We say the agents can collectively determine thatωhas not occurred if there is an agent who knows some subset of¬{ω}; that is, if there is an agent who knows an event which does not contain
ω. The distributed knowledge of E is when all points outside of E are collectively known to have not occurred. This is formalized in Definition 2.7.
Definition 2.7. Fix a state spaceΩ, and letKbe the associated set of knowledge operators.
Define the distributed knowledge aggregator∨: Seq(K)→ Kpointwise at each sequence
(K1, . . . , Kn)∈Seq(K)and eventE ∈2Ω, by
∨(K1, . . . , Kn)E = \
ω /∈E
[
F⊂¬{ω}
n
[
i=1
KiF (2.1)
For a knowledge model(Ω, J,{Kj}
j∈J), the distributed knowledge aggregation∨J : 2Ω →2Ω
is
∨JE = \
ω /∈E
[
F⊂¬{ω}
[
j∈J
KjF
Each stateωis in∨JE when, for each stateωoutsideE, there is some agentj ∈ J and some
eventF 63ωsuch thatj knowsF. That is, for each stateωoutsideE, there is some agent who knows that stateωdid not happen.
The distributed knowledge aggregator admits an alternative representation in terms of collections of known events, as detailed in Lemma 2.7 in Section 2.5. This alterna-tive representation is useful for some of the proofs of properties of the distributed knowledge aggregator.
2.3
Core Properties of Knowledge Aggregators
This section proposes and analyses a selection of regularity properties of aggregators, and analyzes the classical aggregators in terms of these properties. Section 2.3.1 studies properties of knowledge aggregators arising due to their nature as functions which take a variable number of inputs. Section 2.3.2 considers properties related to the level of information held by the agents, and how this relates to the resulting aggregation for different aggregators.
2.3.1
Anonymity, Associativity, and Identity
While in generalJhas a defined order, in many cases it will be sufficient to consider
J as a set of agents. When aggregatorAis anonymous, as in Definition 2.8, then it is enough to think of J as a (multi)-set. As usual, anonymity is the statement that the order of agents in the list does not matter.
Definition 2.8. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. A knowledge aggregator A : Seq(K) → K is anonymous when, for all finite sequences of knowledge operators(K1, . . . , Kn) ∈Seq(K)and all bijective functionsσ : {1, . . . , n} →
{1, . . . , n}, then
A(K1, . . . , Kn) = A(Kσ(1), . . . , Kσ(n))
All of the classical knowledge aggregators in Section 2.2.2 are anonymous. Aggre-gators will fail anonymity when agents are treated differently. If, say, the modeler had a prior belief that Agent 1 was more trustworthy than the other agents, then an ap-propriate knowledge aggregation method would treat Agent 1 differently to the other agents.
While anonymity deals with the order of agents, the associativity condition is that the order of aggregation does not matter. We provide two equivalent definitions of associativity. The traditional definition of associativity for functions which take any finite sequence as input is given by Definition 2.9. Associativity, according to Definition 2.9, is the idea that aggregating the knowledge of all individuals in a single step is the same as aggregating any subset, then adding the other members to the aggregation afterwards. Intuitively speaking, it is a form of path-independence of aggregation.
Definition 2.10 provides an alternative definition of associativity. Associativity, according to Definition 2.10, states that given two or more subpopulations of the set of agents, taking the aggregation of all agents together should be the same as taking the aggregation of each subpopulation, and then aggregating the outcomes. Further, this process should not depend on the particular subpopulations used.
Proposition 2.1 shows that these definitions are equivalent.
Definition 2.9. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. An aggregator A : Seq(K) → Kis associative if, for any (K1, . . . , Kn) ∈ Seq(K), and cutoffs1≤n1 < n2 ≤n, then
where, when n1 = 1, it is understood that K1, . . . , Kn1−1 is the empty list. Similarly when
n2 =n, it is understood thatKn2+1, . . . , Knis the empty list.
Definition 2.10. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. A knowledge aggregatorA : Seq(K) → Kis associative if for any sequence of knowledge operators(K1, . . . , Kn)∈ Seq(K), and any collection of cutoffs0 = n
0 < n1 < n2 <· · · <
nk =n, then aggregating directly over the full list(K1, . . . , Kn), results in the same operator
as is obtained by a two-step process, where first we aggregate all operators over those lists
Kni+1, . . . , Kni+1 separately, and then, in the second step, aggregate thekoutcomes of the first step. Formally
A(K1, . . . , Kn) =A A(K1, . . . , Kn1),A(Kn1+1, . . . , Kn2), . . . ,A(Knk−1+1, . . . , Kn) (2.3)
Proposition 2.1. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. An aggregator A : Seq(K) → Ksatisfies Equation 2.2 if and only if it satisfies Equation 2.3. Therefore, the definitions of associativity given in Definitions 2.9 and 2.10 are equivalent.
Associativity implies that the aggregator is an idempotent operator; that is,AJ =
A(AJ). The classical aggregators of everybody knows, somebody knows, and dis-tributed knowledge are associative aggregators, as shown in Proposition 2.2. This is not the case for the common knowledge aggregator, as information is, in some sense, lost during the aggregation process. Example 2.1 shows that common knowledge may not be associative.
Proposition 2.2. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. The aggregators everybody knows, somebody knows, and the distributed knowledge are associative.
Example 2.1. LetJ ={1,2}, andΩ ={a, b, c, d}. Suppose that:
K1Ω ={a, b, c}, K1{a, b, c}={a}, K1{a}={a}, K1{a, b}={a, b},
K2Ω ={a, b}, K2{a, b, c}={a, b}, K2{a, b}={a, b}, K2{a}={a}.
Then:
fJ{a, b}={a, b}.
Thus, for everys ∈ {1,2,· · · }:
∧JΩ = (
fJ)(s)Ω ={a, b}.
However, forJ1 ={1},J2 ={2}, we find that∧J1Ω ={a}and∧J2Ω ={a, b}. Then
∧(∧J1,∧J2)Ω ={a} 6={a, b}=∧JΩ.
Therefore, the common knowledge aggregator∧: Seq(K)→ Kis not associative.
Where anonymity is concerned with the order of the agents, we can be equally concerned with the labeling of the states. A knowledge operatorKwill, in general, be sensitive to relabeling of the states, in the sense that for a given relabeling of the statesf, thenK◦f 6=f◦K. Aggregators, however, can certainly be independent of the labeling of the states. An aggregator is independent of the labeling of the states if relabeling the states, then applying the aggregator, is the same as applying the aggregator then relabeling the states. An aggregator which is independent of relabeling of the states is said to be label neutral.
Definition 2.11. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. An aggregatorA : Seq(K) → Kis label neutral if, for any bijection f : Ω →Ω, and any
(K1, . . . , Kn)∈Seq(K), then
A=f−1◦A f◦K1, . . . , f◦Kn
where we make the usual abuse of notation thatf(E) ={f(ω)|ω∈E}.
The classical aggregators somebody knows, everybody knows and distributed knowledge are label neutral. An aggregator will not be label neutral if it treats some states differently to others, or, potentially, if it includes some form of composition of knowledge operators. The common knowledge aggregator is not label neutral as it includes composition of knowledge operators. An instance where the common knowl-edge aggregator is not label neutral is in Example 2.2. The synthetic aggregator in Example 2.3 is not label neutral as it treats states differently.
Example 2.2. LetJ ={1},Ω ={a, b, c}. Suppose that
K1{a, b, c}={a, b}, K1{a, b}={a}, andK1E =E otherwise
As |J| = 1, the everybody knows aggregationfJ is just fJ = K1. The common knowledge aggregation∧J has
∧JΩ = K1Ω∩K1K1Ω∩ · · ·={a, b} ∩ {a} ∩ · · ·={a}
Letf : Ω→Ωbe a bijection, wheref(a) =b,f(b) = c, andf(c) =a. The compositionf◦K1
is somewhat ugly, but in particular,
(f ◦K1)(4)Ω ={b}, and(f ◦K1)(5)Ω ={c}
Therefore, forf(J) = (f ◦K1)∈Seq(K),
∧f(J)Ω =
∞
\
s=1
(f ◦K1)(s)Ω
⊂(f◦K1)(4)Ω∩(f◦K1)(5)Ω
={b} ∩ {c}=∅
As∧f(J)Ω = ∅, thenf−1∧f(J)Ω6= ∧JΩ. Thus, the common knowledge aggregator∧is not
label neutral.
We would also like to know under what circumstances, if any, the aggregators have the property that when all agents have the same knowledge operator, then the aggregation returns just this same input operator. An aggregator is ak-identity if, for any collection ofkagents with the same knowledge operator, then the aggregation is the same as the input operators. An aggregator is an identity if it is ak-identity for all
k ∈N.
More generally, consider any subset of operators L ⊂ K. An aggregator is a k -identity on L if, for any collection of k agents with the same knowledge operator, where that knowledge operator is inL, then the aggregation is the same as the input operators. Similarly for an aggregator being an identity onL.
Definition 2.12. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. Let L ⊂ K be a collection of knowledge operators, and k ∈ N. A knowledge aggregator
A: Seq(K)→ Kis ak-identity onLif
A(L, L, . . . , L
| {z }
ktimes
for allL∈ L. AggregatorAis an identity onLif it is ak-identity onLfor allk∈N.
AggregatorAis ak-identity if it is ak-identity onK, and is an identity if it is ak-identity for allk ∈N.
This definition states that the restriction of the aggregator toSeq(L)is the identity. The simple classical aggregators of somebody knows and everybody knows are iden-tities on the full set K, while the more involved aggregators of common knowledge and distributed knowledge are not identities on all ofK. The setsLon which common knowledge and distributed knowledge are an identity are noted in Proposition 2.10.
2.3.2
Relative Informativeness
The four classical knowledge aggregators discussed admit a natural hierarchy of how much information they could be said to admit. Intuitively, it is very difficult for in-formation to be common knowledge, and very easy for inin-formation to be available as distributed knowledge. It is much more likely that somebody knows a piece of information than that everybody knows it. This is given in Lemma 2.1.
Lemma 2.1. Let(Ω, J,{Kj}
j∈J)be a knowledge model. Then, for every eventE ∈ 2Ω, and
every agentj ∈J:
∧J E ⊂fJE ⊂KjE ⊂gJE ⊂ ∨JE (2.4)
This hierarchy suggests an idea of positive and negative aggregators. Positive ag-gregators are those that work to increase the amount that is known, while negative aggregators work to reduce the amount that is known.4 The notion of relative infor-mativeness of knowledge operators is given in Definition 2.13. Inforinfor-mativeness of knowledge operators is a partial order on the set of knowledge operators K, as it is possible that agent1is well-informed in one area, while agent2is informed in another.
Definition 2.13. Fix a state spaceΩ, and letKbe the associated set of knowledge operators.
Operator K1 ∈ K is more informative than operatorK2 ∈ K ifK2E ⊂ K1E for every
event E ∈ 2Ω. Being “more informative than" is a partial order on the set of all knowledge operators.
4In applications in game theory, negative aggregators are most appropriate for modeling behavior in
Definition 2.14. Fix a state spaceΩ, and letKbe the associated set of knowledge operators.
An aggregator A : Seq(K) → K is positive if for all (K1, . . . , Kn) ∈ Seq(K), then
A(K1, . . . , Kn)is more informative thanKi, for alli= 1, . . . , n.
An aggregatorA : Seq(K)→ Kis negative if for all(K1, . . . , Kn)∈ Seq(K), thenKi is more informative thanA(K1, . . . , Kn), for alli= 1, . . . , n.
From Lemma 2.1 the distributed knowledge,∨, and somebody knows,g, are posi-tive aggregators; and common knowledge,∧, and everybody knows,f, are negative aggregators. In fact, somebody knows,f, is the least informative aggregator which is still positive, while everybody knows,g, is the most informative aggregator which is still negative, as shown in Proposition 2.4.
Proposition 2.4. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. An aggregatorA: Seq(K)→ Kis positive if and only if for allK1, . . . , Kn ∈Seq(K), the
operatorA(K1, . . . , Kn)is more informative thang(K1, . . . , Kn).
An aggregatorA: Seq(K)→ Kis negative if and only if for allK1, . . . , Kn∈Seq(K), the
operatorf(K1, . . . , Kn)is more informative thanA(K1, . . . , Kn).
What happens to knowledge aggregations as new agents are added to the model? Positive and negative aggregators differ in what could be considered a null agent to add to the model; that is, an agent who makes no difference to the knowledge aggregation. In the case of a positive aggregator, an extra agent who knows nothing might be considered a null agent to add to the model. The knowledge operator associated with the agent who knows nothing is denoted K∅, and given by K∅E = ∅ for all events
E ∈2Ω. For negative aggregators, adding an agent who believes they know everything
might be considered a null agent. The knowledge operator associated with the agent who believes that they know everything is denoted KΩ, and given byKΩE = Ωfor
all events E ∈ 2Ω. Positive and negative aggregators are called natural when their aggregation does not change due to the introduction of a null agent, as in Definition 2.15.
Definition 2.15. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. A positive aggregator A : Seq(K) → K is naturally positive if A(K1, . . . , Kn, K∅) =
A negative aggregator A : Seq(K) → K is naturally negative ifA(K1, . . . , Kn, KΩ) =
A(K1, . . . , Kn), for all(K1, . . . , Kn)∈Seq(K).
An aggregator A : Seq(K) → Kis natural if it is either naturally negative, or naturally positive.
A cursory examination shows that the classical knowledge aggregatorsf,∧,gand ∨are all natural aggregators. An example of a synthetic (artificial, built-for-purpose) aggregator which is positive but not natural is given in Example 2.3.
Example 2.3. Let Ω = {1,2,3,4}, and let K be the associated set of knowledge operators. Define the knowledge aggregatorA∗ : Seq(K)→ Kso that for any sequence(K1, . . . , Kn)∈
Seq(K), and eventE ∈2Ω,
A∗(K1, . . . , Kn)E = ({n} ∩E)∪
n
[
j=1
KjE
That is,A∗asks whether any agent knows the event occurred, then adds in the number of agents,
if that state is in the event. This is an entirely synthetic aggregator.
Clearly,A∗(K1, . . . , Kn)E ⊃Snj=1KjE. By Proposition 2.4,A∗is positive. However,A∗
is not natural in the sense of Definition 2.15 as, for example,
A∗(K∅)Ω ={1}, whileA∗(K∅, K∅)Ω ={2}
Adding an additional agent with no information has changed the knowledge aggregation. AggregatorA∗is also clearly not label neutral as, for example, for any bijectionf : Ω→Ω
withf(1)6= 1, then
f−1◦A∗(f◦K∅)Ω = f−1◦A∗(K∅)Ω =f−1({1})6={1}
Thereforef−1◦
A∗(f◦K∅)=6 A∗(K∅), and thus,Ais not label neutral.
Knowledge aggregation can also be investigated when agents may learn new in-formation. Fix a collection of agentsJ, and their knowledge operators{Kj : 2Ω →2Ω,
j ∈ J}. Suppose that agents receive a positive knowledge shock, which weakly im-proves their knowledge. This positive shock transforms each operatorKj,j ∈J, into a more informed operatorKej,j ∈J.
An aggregatorA : Seq(K) → Kis increasing if for any pair of sequences (K1, . . . , Kn),
(Ke1, . . . ,Ken) ∈ Seq(K) such that each operator Kei is more informed than Ki, for each
i ∈ {1,· · ·, n}, then the aggregationA(Ke1, . . . ,Ken)is more informed thanA(K1, . . . , Kn).
Formally,
KiE ⊂KeiE, for alli∈ {1, . . . n},E ⊂Ω
=⇒ A(K1, . . . , Kn)E ⊂A(Ke1, . . . ,Ken)E, for allE ⊂Ω
.
While it might be expected that the four classical aggregators are all increasing, this is not the case. The everybody knows, somebody knows, and distributed knowledge aggregators are indeed all increasing, as in Lemma 2.2.
Lemma 2.2. The aggregators everybody knows, somebody knows, and distributed knowledge are increasing operators.
The common knowledge aggregator, however, is not increasing in general. Exam-ple 2.4 gives a pair of sequences of knowledge operators which demonstrates that the common knowledge aggregator is not increasing. The common knowledge aggrega-tor is increasing if certain reasonable assumptions are made on the input knowledge operators. This is explored in Proposition 2.12.
Example 2.4. LetΩ ={a, b, c}and operatorsK,Ke ∈ Kgiven by
K{a, b, c}={a}, K{a, b}=∅, KE =E otherwise
e
K{a, b, c}={a, b}, Ke{a, b}=∅, KEe =Eotherwise
Operators K,Ke differ only on{a, b, c} whereK{a, b, c} ⊂ Ke{a, b, c}. Thus, operator Ke is
more informed than operator K. However, asKeKe{a, b, c} = ∅, the corresponding common
knowledge aggregations are
∧(K){a, b, c}={a}, ∧(K){a, b}=∅, ∧(K)E =Eotherwise
∧(K)e {a, b, c}=∅, ∧(K)e {a, b}=∅, ∧(K)Ee =Eotherwise
Aggregations∧(K),∧(K)e differ only on{a, b, c}where∧(K){a, b, c} ⊃ ∧(Ke){a, b, c}. Thus,
operator∧(K)is more informed than operator∧(K)e . Therefore, the common knowledge
If an aggregator is natural and increasing, as is the case for many of our example aggregators, then the aggregator will behave nicely with the addition of new agents. In particular, for positive aggregators, new agents will mean aggregated information is more informative as more agents are added; while for negative aggregators, new agents will cause a reduction in aggregated information.
Proposition 2.5. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. Let(K1, . . . , Kn)∈Seq(K)andm < n.
If an aggregatorA: Seq(K)→ Kis naturally positive and increasing, thenA(K1, . . . , Kn) is more informative thanA(K1, . . . , Km). Similarly, ifA: Seq(K)→ Kis naturally negative and increasing, thenA(K1, . . . , Km)is more informative thanA(K1, . . . , Kn).
Finally we consider a notion of stationarity for knowledge aggregators, as a coun-terpart to the notion of naturalness given in Definition 2.15. An aggregator is natural if adding an extreme agent does not change the knowledge aggregation. Similarly, we say an aggregator is stationary if the aggregation does not change when adding a new agent who is both weakly less informed than some existing agent, and weakly more informed than an existing agent.
Definition 2.17. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. An aggregatorA: Seq(K)→ Kis stationary if for any sequence(K1, . . . , Kn)∈Seq(K), and any K∗ such that K∗ is less informed than some K0 ∈ (K1, . . . , Kn), and K∗ is more informed than someK00 ∈(K1, . . . , Kn), then
A(K1, . . . , Kn) = A(K1, . . . , Kn, K∗)
Stationarity is closely related to the property of being an identity. In particular, if aggregatorAis a 1-identity on someL ⊂ K, and is stationary, then it is an identity on L.
Proposition 2.6. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. LetL ⊂ K, and aggregatorA: Seq(K)→ Kbe a 1-identity onL, and stationary. ThenA is an identity onL.
Example 2.5. Let Ω = {1,2,3,4}, and let K be the associated set of knowledge operators. Define the ‘at least two agents know’ knowledge aggregator A2 : Seq(K) → K such that for
any sequence(K1, . . . , Kn)∈Seq(K), then for each eventE ∈2Ω,
A2(K1, . . . , Kn)E =
[
i,j∈{1,...,n}
i6=j
KiE∩KjE
That is,A2 asks whether any pair of agents knows the event occurred.
Let K ∈ K be a knowledge aggregator with K 6= K∅. By construction, A2(K) = K∅,
whileA2(K, K) = K. AsK is both more informed and less informed thanK, andA2(K)6=
A2(K, K), the aggregatorA2 is not stationary.
In fact, the aggregatorA2 is ak-identity for allk ≥ 2; just not a1-identity, and so not an
identity aggregator.
2.4
Logic Properties of Knowledge Aggregators
There are a variety of assumptions often made to restrict the available knowledge operators to those which satisfy certain logical properties. The strongest assumption, which is also the most common, is to restrict knowledge operators to those which admit representation by a partition of the state space. In such a model, the state space is partitioned, where the agent is unable to distinguish states in the same partition element, but can distinguish between partition elements.
A weaker, but still common, assumption is the knowledge correspondence model. In this model of knowledge, in each state of the world the agent receives a signal which informs them of the the states they consider possible.
These restrictions on the state space are further broken down into the Modal Logic S5 system. This is a list of five rationality assumptions which together imply a partition representation, but which can also be investigated individually.
2.4.1
Partitions and Correspondences
not possible. Each knowledge partitionπis associated with a knowledge operatorKπ
according to the formula
KπE ={ω∈Ω|π(ω)⊂E} (2.5)
This equation says that if partition π represents the agent’s information, then KπE
should be the set of states where every state the agent considers possible is contained in the eventE. We say an operator is partitional if there exists some partition which generates the operator using Equation 2.5.
Definition 2.18. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. An operatorK ∈ Kis partitional if there exists some partitionπofΩsuch thatK =Kπ,
whereKπ is given by Equation 2.5. The set of partitional operators is denotedKP.
Remark 2.1. A partitional knowledge operator will necessarily satisfy certain regularity con-ditions. In particular, any partitional knowledge operatorK : 2Ω →2Ωwill satisfyKΩ = Ω,
K(E ∩F) = KE ∩KF, KE ⊂ E, KE ⊂ KKE and ¬KE ⊂ K(¬KE) for all events
E, F in2Ω. Moreover, any knowledge operator satisfying these properties is partitional. This
will be discussed further in Section 2.4.2.
Turning to the question of knowledge aggregators; if the knowledge operators of all agents are partitional, which knowledge aggregations will also be partitional? This question has a surprising answer. The relatively simple aggregators of somebody knows,g, and everybody knows,f, do not preserve this property of being partitional. That is, even if all agents have the very strong rationality property of a partitional information structure, nonetheless very simple statements like ‘does somebody know this’ may not have such rationality properties. Example 2.6 provides a simple model where this is the case. Proposition 2.7 shows that the more developed aggregators of common knowledge,∧, and distributed knowledge,∨, are partitional-preserving.
Definition 2.19. Fix a state spaceΩ, and letKbe the associated set of knowledge operators.
Example 2.6. LetJ ={1,2},Ω = {a, b, c}, and
K1{a}=K1{b}=∅, K1{a, c}=K1{b, c}={c}, K1E =E otherwise
K2{b}=K2{c}=∅, K2{a, b}=K2{a, c}={a}, K2E =E otherwise
Operator K1 is a partitional operator given by the partitionπ1 = {{a, b},{c}} according to Equation 2.5. Similarly, operator K2 is a partitional operator given by the partition π2 =
{{a},{b, c}}.
The somebody knows aggregationgJ has
gJ({a, b} ∩ {b, c}) = gJ{b}=∅
gJ{a, b} ∩gJ{b, c}={a, b} ∩ {b, c}={b}
AsgJ({a, b} ∩ {b, c})=6 gJ{a, b} ∩gJ{b, c}, by Remark 2.1, the somebody knows aggregation
gJis not partitional in this case. Therefore, the somebody knows aggregatorgis not partitional
in general. Similarly, the everybody knows aggregationfJ has
fJ{a, b}={a, b} ∩ {a}={a}
fJ{a}=∅ ∩ {a}=∅
Asf{a, b} 6⊂ff{a, b}, by Remark 2.1, the everybody knows aggregationfJis not partitional
in this instance. Thus, the everybody knows aggregatorfis not partitional.
Proposition 2.7. The aggregators common knowledge and distributed knowledge are both partition-preserving aggregators.
The correspondence knowledge framework is a middle ground between the more general universe of knowledge operators and the more restrictive universe of partitions. A knowledge correspondence is a functionγ : Ω→2Ω. The usual interpretation is that,
at every stateω∈Ω, the agent considers as possible exactly those states inγ(ω), ruling out all states that do not belong toγ(ω). In other words, at stateω∈Ω, the agent thinks that an eventE is sure to happen if and only ifγ(ω)⊂E, and is sure that eventEdoes not happen if and only ifE∩γ(ω) =∅.
Each knowledge correspondence γ is associated with a knowledge operator Kγ
according to the formula
This equation says that if correspondence γ represents the agent’s information, then
KγE should be the set of states where every state the agent considers possible is
con-tained in the eventE. Definition 2.20 states that an operator is a correspondence oper-ator if there exists some correspondence which generates the operoper-ator using Equation 2.6.
Definition 2.20. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. An operator K ∈ K is a correspondence operator if there exists some correspondence γ : Ω → 2Ω such that K = K
γ, where Kγ is given by Equation 2.6. The set of correspondence
operators is denotedKC.
An operatorK : 2Ω →2Ωis a correspondence operator so long as it satisfiesKΩ = Ω,
andK(E ∩F) = KE ∩KF for all eventsE, F ∈ 2Ω, as shown in Lemma 2.3. These properties are explored further in Section 2.4.2.
Lemma 2.3. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. An operatorK ∈ Kis a correspondence operator if and only ifKΩ = ΩandK(E∩F) = KE∩KF for all eventsE, F ∈2Ω.
The correspondence framework is a strict generalization of the partition framework. Lemma 2.4 shows that any knowledge partition is just a knowledge correspondenceγ
that satisfies the additional properties that: P.1: ω ∈γ(ω), for everyω ∈Ω.
P.2: For everyω, ω0 ∈Ω, the setsγ(ω)andγ(ω0)either coincide or have no element in common.
Lemma 2.4. Fix a state spaceΩ, and letKbe the associated set of knowledge operators, and let
γ : Ω→2Ω be a knowledge correspondence.
Correspondenceγ satisfies properties P.1 and P.2 if and only ifKγis partitional. In general,
KC ⊂ KP.
example, all input operators were partitional, so by Lemma 2.4 were also correspon-dence operators. However, the output operator failed to haveK(E∩F) =KE ∩KF, and so, by Lemma 2.3, was not a correspondence operator. The remaining classical aggregators common knowledge, distributed knowledge and everybody knows all preserve the property of being a correspondence operator.
Definition 2.21. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. An aggregator A : Seq(K) → K is correspondence-preserving if, for all sequences of correspondence knowledge operators (K1, . . . , Kn) ∈ Seq(K
C), the knowledge aggregation
A(K1, . . . , Kn)is also a correspondence operator.
Proposition 2.8. The aggregators common knowledge, distributed knowledge, and everybody knows, are all correspondence-preserving aggregators.
2.4.2
Modal Logic’s S5 Axioms
The partitional and correspondence assumptions on knowledge operators are repre-sentation assumptions which do not, within their definition, contain clear information on what aspects of rationality are being assumed, nor do they make clear why we might think an agent would be partitional or have a correspondence operator. The S5 logic system is a series of rationality assumptions which are direct restrictions of the knowledge operator itself and are individually justifiable to some extent. While a modeler might hope that their agent will satisfy each of the S5 axioms, evidence from behavioral economics seems to suggest that these axioms are regularly broken in practice.
K.0 (Awareness). LetK0 ={K ∈ K |KΩ = Ω}.
Awareness requires that, at every state, agent j knows that eventΩoccurs. This property rules out the existence of subjective states. Agents know perfectly well the state space.
K.1 (Monotonicity). LetK1 ={K ∈ K |K(E∩F)⊂KE∩KF, E, F ∈2Ω}.
Monotonicity is equivalent to the requirement that E ⊂ F ⇒ KjE ⊂ KjF, for
all eventsE, F ∈ 2Ω. This property states that if a agent knows a specific event has
K.2 (Conjunction). LetK2 ={K ∈ K |K(E∩F)⊃KE∩KF, E, F ∈2Ω}.
Conjunction is a rationality condition on the agents. It states that if a agent knows that eventsE andF happen individually, then she knows that the specific event that is the intersection ofE andF has indeed occurred.
K.3 (Truth). ConsiderK3 ={K ∈ K |KE ⊂E, E ∈2Ω}.
This property says that if agentjknows eventE, thenE occurs; that is,j can only learn truths.
K.4 (Positive Introspection). LetK4 ={K ∈ K |KE ⊂KKE, E ∈2Ω}.
Some authors refer to this property as Transparency. It indicates that agents are aware of their own knowledge.
K.5 (Negative Introspection). LetK5 ={K ∈ K | ¬KE ⊂K(¬KE), E ∈2Ω}.
Some authors refer to this as Wisdom. It indicates that agents are aware of their own limitations.
If an agent’s knowledge operator satisfies all the S5 axioms, then it is a partitional operator in the style of Definition 2.18. Similarly, any partitional operator will satisfy all the S5 axioms. This was mentioned earlier in Remark 2.1, and is the main result of Bacharach [1985].
Proposition 2.9. (Bacharach’s Partition Theorem (Bacharach [1985])) A knowledge operator
K satisfies all S5 axioms if and only if it is a partitional operator. That is
KP =K0∩ K1∩ K2∩ K3∩ K4∩ K5
Similarly, Lemma 2.3 states that an operator is a correspondence operator if and only if it satisfies Awareness, Monotonicity, and Conjunction. That is
KC =K0∩ K1∩ K2
We promised earlier to identify the collections of operators L ⊂ K on which the classical aggregators are an identity.
Proposition 2.10. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. Aggregators everybody knows and somebody knows are identities on K. The common knowledge aggregator is an identity onK4. The distributed knowledge aggregator is an identity
Section 2.4.1 discussed whether aggregators had preservation properties in terms of partitional and correspondence operators. The same questions can be asked with regard to each of the S5 axioms. That is, if the knowledge operators of all agents satisfy any of the S5 properties, which knowledge aggregations will also satisfy this property? A related property is that of ‘forcing’. A aggregator ‘forces’ a property if the aggregation necessarily has some property, even if the input operators do not have this property. More generally, we can talk aboutL-preserving, andL-forcing aggregators for any subset of knowledge operatorsL ⊂ K.
Definition 2.22. Fix a state spaceΩ, letKbe the associated set of knowledge operators, and L ⊂ K.
An aggregatorA: Seq(K)→ KisL-preserving if, for all sequences of knowledge operators
(K1, . . . , Kn)∈Seq(L), the knowledge aggregation
A(K1, . . . , Kn)is also inL.
Definition 2.23. Fix a state spaceΩ, letKbe the associated set of knowledge operators, and L ⊂ K.
An aggregator A : Seq(K) → Kis L-forcing if, for all sequences of knowledge operators
(K1, . . . , Kn)∈Seq(K), the knowledge aggregation
A(K1, . . . , Kn)is inL.
Clearly, ifLis forced by some aggregatorA, then it is also preserved byA. Propo-sition 2.11 contains a complete classification of the classical aggregators as either L-preserving,L-forcing, or neither, for the sets of knowledge operators satisfying each of the S5 axioms. While both distributed knowledge and common knowledge pre-serve the S5 axioms collectively, as in Proposition 2.7, only the distributed knowledge preserves the axioms individually. Surprisingly, the common knowledge aggregator does not force, or even preserve, the Positive Introspection property. This last fact is explored in greater detail in Chapter 3.
∨ g f ∧
K0 F P P P
K1 F P P P
K2 F No P No
K3 P P P P
K4 P No No No
[image:44.595.145.451.87.305.2]K5 P No No No
Table 2.1:S5 Preservation
2.4.3
Monotonicity
The Monotonicity axiom, K.1. can be considered to be a very reasonable assumption on the set of knowledge operators. However, it is also an extremely powerful assumption for producing more regular results. This short section assumes Monotonicity of all knowledge operators, in order to produce stronger results on the knowledge aggrega-tors. Lemma 2.5 gives a more concise form of the distributed knowledge aggregator. Lemma 2.6 shows that the somebody knows aggregator preserves Positive Introspec-tion. Proposition 2.12 shows that the common knowledge aggregator is increasing.
If all agents’ knowledge operators satisfy Monotonicity, then the distributed knowl-edge aggregator∨admits a much cleaner representation.
Lemma 2.5. Fix a state spaceΩ, and letKbe the associated set of knowledge operators. Let ∨ : Seq(K) → K be the distributed knowledge aggregator given by Equation 2.1. Let (K1, . . . , Kn) ∈ Seq(K
1) so that all operators satisfy Monotonicity. Then for all events
E ∈2Ω,
∨(K1, . . . , Kn)E = \
ω /∈E
[
j∈J
Kj¬{ω} (2.7)