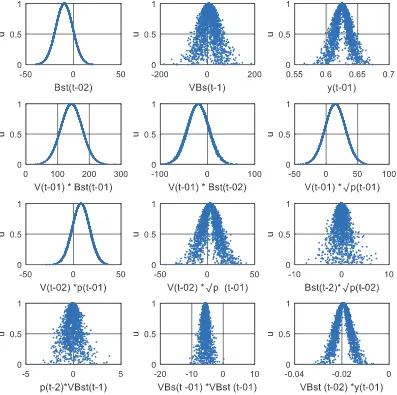
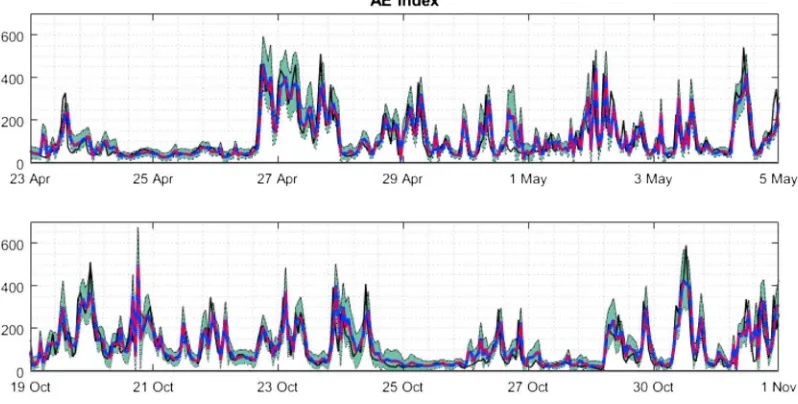
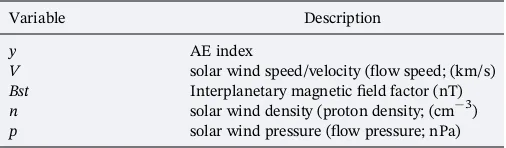
System identification and data-driven forecasting of AE index and prediction uncertainty analysis using a new cloud-NARX model
17
0
0
Full text
Figure



+6
Related documents