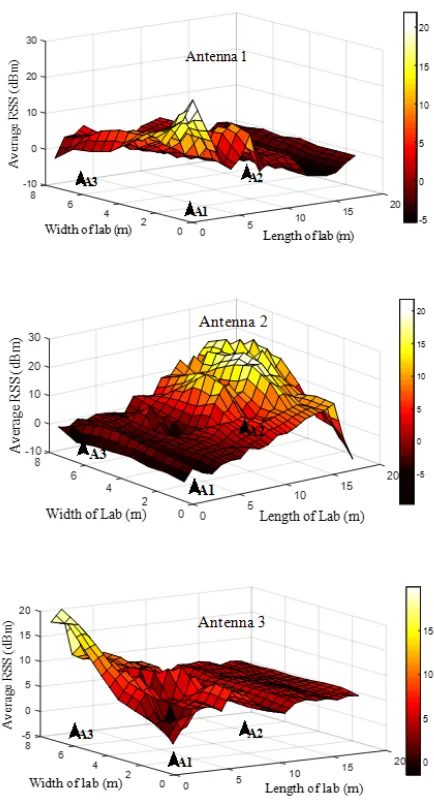
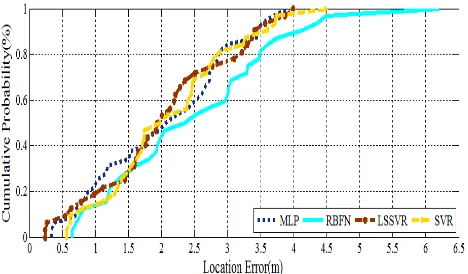
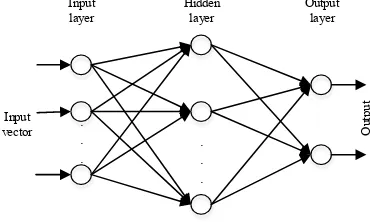
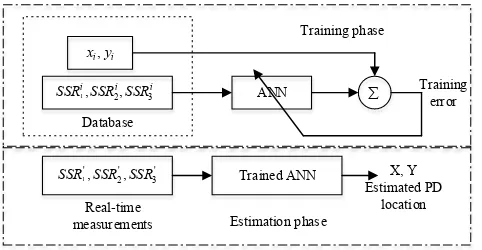
Radio location of partial discharge sources : a support vector regression approach
Full text
Figure
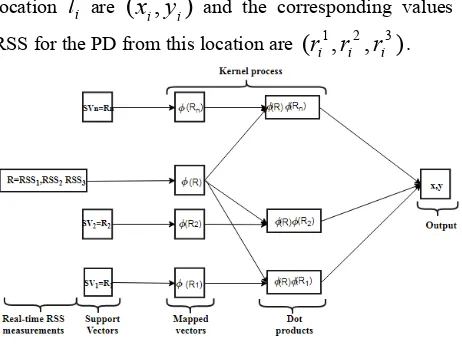
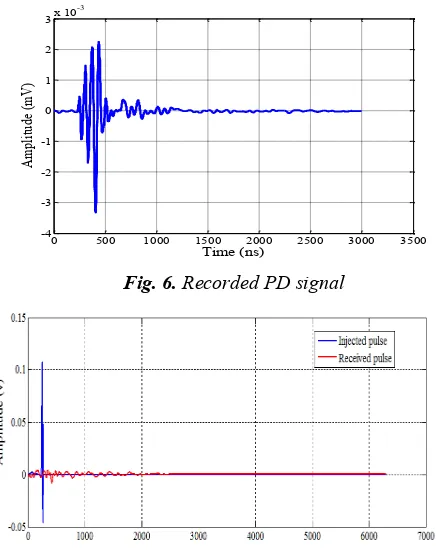
Related documents
The instrument contained 13 attitudinal statements related to the newsletter received, measured on a seven-point Likert scale: reactions to the site (newsletter frequency, drop
For the poorest farmers in eastern India, then, the benefits of groundwater irrigation have come through three routes: in large part, through purchased pump irrigation and, in a
As inter-speaker variability among these the two groups was minimal, ranging from 0% to 2% of lack of concord in the 21-40 group and from 41% to 46% in the 71+ generation, we
This research focused on music programs, both choral and instrumental in high schools under District B specifically. The first question that I intended to answer was whether or
Through this service offering, Capita IB Solutions will provide maintenance and support services for financial applications including Integra Enterprise and Oracle E-Business
The PROMs questionnaire used in the national programme, contains several elements; the EQ-5D measure, which forms the basis for all individual procedure
Compared to greater Pakistan, the FATA is suffering from lower levels of investment in health capital, education and economic development?. All of these factors contribute to
The key segments in the mattress industry in India are; Natural latex foam, Memory foam, PU foam, Inner spring and Rubberized coir.. Natural Latex mattresses are