The examination of teacher student communication process in the classroom: mathematical communication process model
Full text
Figure
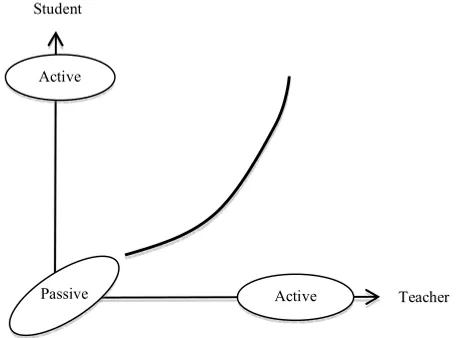

Related documents
For this, OpenFPM provides an encapsulated serialization/de-serialization sub-system that is used by each processor locally in order to serialize the local pieces of a distributed
March 2020 - A number of EAA chapters have contacted headquarters regarding guidance, options, and cautions regarding chapter events, in conjunction with the coronavirus.. Here is
Knowledge and application of Public Service Act, Public Service Regulations, Labour Relations Act, Skills Development Act, Basic Conditions of Employment Act,
One potential moderating factor is perceived control.(29-31) Perceived control is associated with anxiety level.(29,32,33) In a variety of cardiac patients, including heart
In the moderately fertile soil, compost addition significantly increased plant height, leaf number, and corn yields (Table 7)+. Plant height at the highest rate was about two
Any financial institution – be it a securities firm, an insurance company, a hedge fund, a private equity firm, or a bank holding company – which is not now subject to the
The clean screen is not available for HMI devices with touch screen and function keys. In this case, configure a screen without operator controls,
Students with a major subject in medical electronics can take their minor subject in electronics, digital signal processing, measurement technology, digital and computer