Relay Auto Tuning Of Parallel Cascade Controller
Full text
Figure
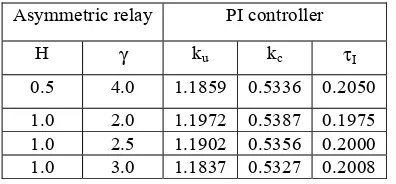
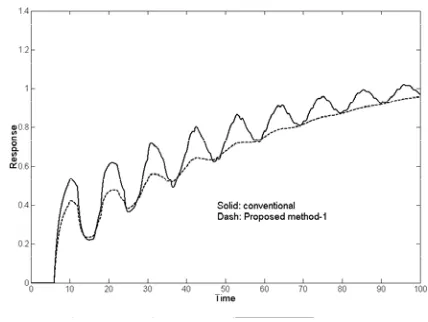
Related documents
The Insurance Institute for Highway Safety (IIHS) is concerned about the slow pace of rulemaking by the Federal Motor Carrier Safety Administration (FMCSA) regarding the
In the star-structured model,
The PREMIER study: a multicenter, randomized, double-blind clinical trial of combination therapy with adalimumab plus methotrexate versus methotrexate alone or adalimumab alone
Probability distributions were estimated for several random variables including the time between machine breakdowns, processing time on the machines, and number of patients;
Virtually every company has basic Internet service installed for web access and other applications, and if there is capacity available over those links, SIP trunking services can
Figure 7: The 95% joint confidence region of the sensitivity and the specificity at the optimal cut-off point associated with the Youden index for marker HPX. Since both
ENVIRONAGE birth cohort, we have studied placental epigenetic signatures in association to air pollution on dif- ferent levels, from global DNA methylation, gene-specific
Coefficient Of Performance actual terendah sebesar 2,19, tertinggi sebesar 7,2, Coefficient Of Performance ideal terendah sebesar 5,90, tertinggi sebesar 21,31, Nilai efisiensi