Development of PSO for tracking Maximum Power Point of Photovoltaic Systems
Full text
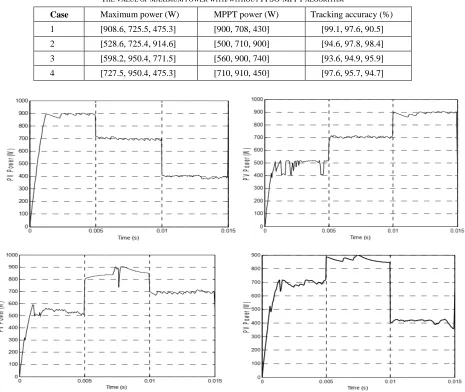
Figure



Related documents
повышается также скорость входа протонов в матрикс (рис.. Влияние МрТр на трансмембранный обмен ионов в митохондриях. Открывание МРТР, как уже было показано нами
Отже, нами встановлено, що відсутність вітаміну А в організмі з пухлиною, порівняно з онкогенезом за нормальної забезпеченості цим есенціальним нутрієнтом,
Results suggest that the probability of under-educated employment is higher among low skilled recent migrants and that the over-education risk is higher among high skilled
Field experiments were conducted at Ebonyi State University Research Farm during 2009 and 2010 farming seasons to evaluate the effect of intercropping maize with
Materials and Methods: The specificity of the assay was tested using reference strains of vancomycin-resistant and susceptible enterococci.. In total, 193
Molecular detection of mutations associated with first- and second-line drug resistance compared with conventional drug susceptibility testing of Mycobacterium
19% serve a county. Fourteen per cent of the centers provide service for adjoining states in addition to the states in which they are located; usually these adjoining states have