A Bayesian mixture modelling approach for spatial proteomics.
Full text
Figure
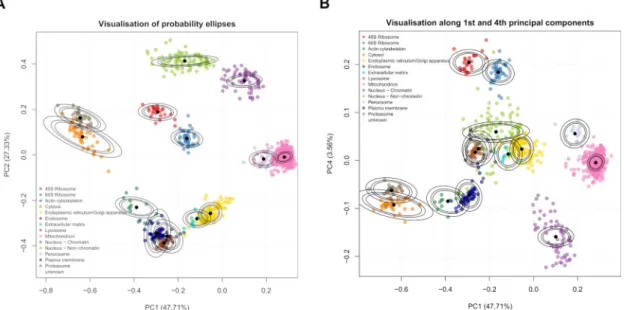

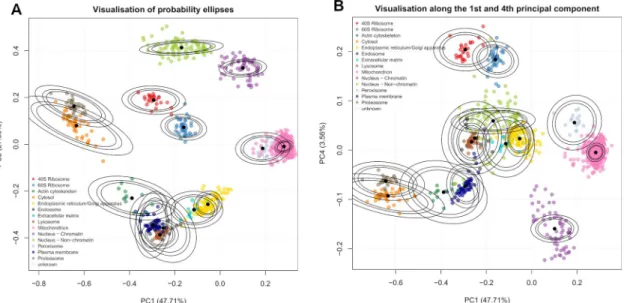

Related documents
The experiments were executed on an Intel Xeon Skylake-SP, which is the first Intel processor to implement a mostly non-inclusive last-level cache (LLC). We present a classification
1 Alcohol Treatment Center, Lausanne University Hospital, Lausanne, 1011, Switzerland; 2 Department of Population Health, New York University School of Medicine, New York, NY
Product Feature Component Tags Description Oracle Field Service Wireless Other Change_Task_ Assignment_St atus Task Assignme nt, Task Status, Wireless. This component changes task
Transformational Leadership was found to strongly and positively determine both the “followers’ perceived leadership effectiveness” and “followers’ job satisfaction”, while
By integrating access to the Journal Locator into our OPAC, our customers can easily locate a database that indexes a journal we have that they are interested in or find out where
1) To assess the level of maternal knowledge about folic acid among women attending well baby clinic in ministry of health primary health care centers in
As such, the current paper will differentiate psychological assessment from psychological testing, identify standards in the conduct of assessment in the
Table 3 shows the top 5 financial institutions, in terms of in-degree and out-degree, found using our time-varying framework with the restricted data sample.. Concurrent with





