Optimization with Fuzzy Constraints in Agricultural Production Planning

(1)

ELSEVIER

Optimization with Fuzzy Constraints in

Agricultural Production Planning

Arnold Sher & Ilan Amir

Faculty of Agricultural Engineering, Technion, Haifa, Israel (Received 8 June 1992; accepted 10 July 1993)

A BSTRA C T

Agricultural production systems are operated under severe uncertainty. One possibility in coping with the uncertainty in the decision-making process, is to create several plans for different expert assumptions of the unpredictable factors dominating the production, to evaluate the expected value of each plan and to select the largest one. This can be done by using linear programming ( LP).

In the suggested method, as in the above mentioned one, L P is used as the first stage of the decision-making process. However, in this method,

we use the LP's post-optimal sensitivity analysis (POSA). POSA's insen- sitivity limits o f the decision variables of the various solutions are used to create a set of two-sided non-equivalent inequalities. On the basis o f this set and a fuzzy solution of a system o f inequalities, fuzzy constraints are formulated. An algorithm to optimize a linear objective function with varied coefficients subjected to fuzzy constraints has been developed and is presented.

The approach and the method are introduced and demonstrated using an unirrigated farm whose production is dominated by unpredictable rainfall. To evaluate the method, its production and the regular LP production plans were compared, with a significant advantage to the suggested method

I N T R O D U C T I O N

Agricultural production is dependent on many factors that are not fully known quantitatively and, therefore, are not fully controllable (e.g. weather, marketing, resource availability). These factors lead to uncer-

(2)

422 Arnold Sher, llan Amir

tainty, particularly in the processes of planning and operation of agricultural production systems.

Several approaches have been published suggesting methods to cope with the uncertainty involved in agricultural systems (Charnes & Cooper 1963; Amir et al., 1978, 1991; Thangavadivelu & Colvin, 1991, and more). Most of these approaches use linear programming (LP) as an appropriate tool to optimize systems with a very large number of decision variables. One of the advantages of LP, when applied to stochastic agricultural systems, is its post-optimal sensitivity analysis (POSA). Among other features, POSA provides calculated information of marginal (dual) values and ranges of insensitivity of the optimal solution to changes in the decision variables, the resources and the coefficients of the objective function. When these features are used, POSA becomes an appropriate, powerful tool for the decision maker to deal with the inherent stochastic of real systems (Amir et al., 1978).

A planning approach based on POSA is the so-called SALM, a sequen- tial ad-hoc linear model (Amir et al., 1978), that calls for a frequent comparison between the planning and the actual system, and planning again when the actual values of the factors are not within the ranges of insensitivity, as calculated by POSA. To carry out the comparison, Amir et al. (1991) suggested combining SALM with expert system models (ES) in order to process the data of the factors, gathered from the system, with formats pertinent to LP. The processing of the data, mainly for estimation of the expected income, usually requires non-algorithmic methods and procedures based on subjective preferences. The combined model (SALM and ES) is ISFARM--an integrated system for farm management (Amir et al., 1991, 1993). Its basic approach is to plan the system by LP, using the best data available, to monitor continuously the real system by direct measurements and to prepare and process the data by ES, to com- pare the planning with the actual system and then to decide whether to continue with the current plan or to run a new and updated plan.

One of the limitations of the above mentioned approaches, including ISFARM, is the quality of the data used for LP in the planning stage to reach an optimal plan. For these approaches it is clearly suggested to use the 'best data'. In ISFARM (Amir et al., 1993), for example, no particular method for data to be used in the LP formulation was specified.

(3)

Optimization with fuzzy constraints in production planning 423

This definition is used in this work to grade several possible plans of an unirrigated farm, that are dependent on probabilities of rainfall. Each plan is optimal, resulting from an LP run, indicating, among other factors, the sizes of crop activities. The ranges of optimality of the activities for every solution (plan), calculated by POSA, are graded by the probabilities of the corresponding amounts of the annual rainfall. The intersection of the ranges, which belong to more than one probability, are, therefore, graded by the sum of probabilities in the intersection zone of insensitivity. Then an objective function is calculated at each of the comer points of the various probability zones. Both the value of the objective function and the probability of the solution are evaluated at every c o m e r point. Then the expected value of each of the solutions is calculated and the optimum in the multidimensional space is found to be the maximum of the expected values.

The paper presents the general approach and demonstrates it on an unirrigated farm. The mathematical model will be divided into two subjects: (a) The LP sensitivity analysis; and (b) the fuzzy set approach.

T H E L I N E A R P R O G R A M M I N G SENSITIVITY A N A L Y S I S

A problem to be solved by LP can be formulated as follows:

Extremum Z = F.X (1)

subject to A.X ___ B

X > 0

where Z is the value of the objective function to extremize; F is a vector of coefficients; X={xi} is a vector of decision variables, i = 1 .... ,n; A is a n x m technological matrix; and B is a vector of the restrictions.

The optimal solution is Z* with X* and B*.

The validity of the optimum of the solution is maintained as long as the following eqns (2) and (3) are satisfied

Fb D-l > 0 (2)

D-1Bb _>

0 (3)

where D -1 is the inverse basis matrix of the optimal solution. Fb and Bb are the updated vectors of F and B, respectively.

(4)

424 ArnoM Sher, Ilan Amir

the optimal basis will not change. The value of the objective function, however, will be reduced by the product of the marginal value and the deviation from the optimal value of the factor (but still within the ranges of insensitivity).

POSA, calculated by eqns (2) and (3), is part of the information provided by LP as a problem solver. (For further details see Amir

et al.,

1978.)

P L A N N I N G OF AN U N I R R I G A T E D F A R M - - D E M O N S T R A T I O N

The approach and the method will be demonstrated using an unirrigated farm typical to Israel, so as to make the method clearer and to evaluate it by comparison with the regular LP method without fuzzy constraints.

Formulation of the problem--unirrigated farm

The total area of the farm is 100 ha. Five candidate unirrigated crops are considered for growing: cotton--x~, wheat--x 2, barley--x3, chick p e a - - x4, and oats--x 5. The yields of these crops are strongly dependent on the amount of rainfall during the winter. However, different crops have different sensitivity to water amounts. Therefore, the net income of the crops also changes differently with rainfall.

From past experience, in the region where the farm is located (Jezreel Valey, Israel), the yields of the crops as a function of annual rainfalls and the probabilities of annual rainfalls are shown in Table 1.

The objective function is a maximization of the net income of the farm

Zj

= ~ Y~ij (4)

J

where

Zj

is the value of the objective function from the jth amount of rainfall ($);

xij

is the area of the ith crop for the jth amount of rainfall (ha); and yu is the net income of the ith crop for the jth amount of rainfall (S/ha);

The net income Y0 is calculated by

= Y o P , - E U (5)

where

Yo

is the yield of the ith crop under the jth amount of rainfall (ton/ha); P; is the market price per unit weight of the ith crop (S/ton); and

E o.

is the costs of the ith crop and the jth amount of rainfall (S/ha).

(5)

TABLE 1

Crop Yield (ton/ha), Price (S/ton) and Probabilities o f Annual Rainfall

j = l j = 2 j = 3 j = 4 j = 5 j = 6

Annual rainfall

range (mm) >600 500----600 400--500 3 0 0 4 0 0 200---300 <200 Price Pi Rainfall average

rj (mm) (650) (550) (450) (350) (250) (150) (S/ton)

Crops

Cotton x I 1.8 1.8 1-8 1.4 1-0 0

Wheat x 2 5.0 6-0 4.5 3.0 1.5 0

Barley x3 3.0 3.5 3-5 3.0 2.0 0

Chick-pea x4 1.8 2.0 2-0 1.5 1.0 0

Oats x5 8.0 9.0 10.0 8.0 5.0 1.0

Probability Aj 0-07 0.16 0.32 0.27 0.14 0.04

825 165 135 320 90

* which is the area o f the ith crop cluded the optimal mix o f activities x U,

in the j t h optimal solution (annual rainfall).

The farm planning was run six times, one for every annual rainfall, using D H L L P , an LP package for the personal computer. The net income o f the crops, y~, for the various crops were calculated using eqn (5). The outputs o f the six runs, starting from the m a x i m u m rainfall, include the optimal solutions, the dual activities and the limits o f insensitivity for each factor in the problems, as presented in Table 2. This o u t p u t has been used as input for the fuzzy constraints, as explained subsequently.

As can be seen from Table 2, there are intersections between ranges o f insensitivity o f a crop under various rainfalls. F o r example, the ranges o f insensitivity o f Xl are: less than 550 m m (550 m m is a representative value o f the group 500-600 m m o f rainfall) from 28 to 36 ha, and less than 450 m m from 21.43 to 33 ha. Therefore, in this case, the intersection between these two ranges is 28-33 ha. The probability o f the intersection applies to both ranges and, therefore, is the sum o f the probabilities o f the individual ranges, i.e. 16 + 32 = 48%. In other words, any area o f x~ in the intersection o f the insensitivity ranges, is optimal under both rainfalls and, therefore, its probability o f realization is 48%.

The ranges o f insensitivity are linear constraints that form a hyperplane in the n-dimensional space o f the problem (in our case, five dimen- sions according to the n u m b e r o f crops). As for an LP problem in this hyperplane, here also the optimal solution can be found at one o f the corner points.

(6)

426 Arnold Sher, llan Amir

TABLE 2

Optimal Areas of Crops and their Ranges of Insensitivity

j 1 2 3 4 5 6

Rainfall rj (650) (550) (450) (350) (250) (150) Variables Data Probabilities Aj

x i o f L P

0.07 0"16 0"32 0"27 0.14 0"04

OP 23 32 32 20 20 0

Xl ~1 22.86 28 21-43 0 18.57 0

h i 28 32 32 21.71 21.43 oo

~1 478 500 454 410 247 0

OP 20 10 0 20 0 0

X 2 aj2 19 10 0 12 0 0

b~2 22 ~ ~ 26 ~

y~ 180 165 165 154 74 0

OP 20 20 20 12 10 0

X3 ~3 0 0 0 12 0 0

bj3 21 40 25 ~ ~

YO 105 115 115 98 81 0

OP 20 20 20 20 20 0

x 4 aj4 19.78 13.33 0 0 16.67 0

bj4 28.33 26.67 21.67 24 23-33

70 360 380 368 312 112 0

OP 17 0 3.33 28 50 100

x 5 aj5 17 0 3.33 24 50 0

bj5 . . . . . 153-33

70 85 90 90 82 82 43

OP = Optimal values of xi according to LP; aji = lower limit; bji = upper limit; oo = un- bounded; Y0 = coefficient of objective function of crop i for rainfall j.

in the literature any publication that suggests an adequate algorithm to solve a problem under fuzzy constraints with a varied objective function; and (b) determination of the value of the coefficient of the objective func- tion at a corner point as an intersection of several solutions.

For (b), the approach adopted to determine the value of the objective function vector at a corner point is based on the weighted average o f the vectors appearing in the intersection o f insensitivity domains.

[image:6.468.60.409.67.439.2]

(7)

come to a concordance of expert estimates, i.e. to obtain a certain gener- alised solution on the basis of particular solutions.

THE F U Z Z Y P R O G R A M M I N G PROBLEM BASED ON F U Z Z Y SOLUTION OF INEQUALITY SYSTEMS

The notion of a fuzzy solution of unequality systems

Expert estimates in the form of points of n-dimensional space are most popular in practical applications. However, point description of a poorly defined object by few experts does not give adequate representation since it does not allow one to judge the object's degree of indeterminacy due to the small number of experts. At the same time, an expert is sometimes unable to describe such an object in fuzzy set form in multidimensional space.

The help of expert judges is solicited in a poorly formalized (little stud- ied) situation. One of the possible ways of representing an expert judge- ment (evaluation) is by specifying a certain sharply defined region in the variable space by a system of inequalities. A consistent collective evaluation is usually obtained by taking the intersection of the solutions of the individual inequalities.

This consistency principle, however, ignores many specific features of real-life problems. In particular, it ignores possible differences on the importance (weight, necessity) of the different inequalities in the system, whereas real-life constraints often differ in this respect. Moreover, the accepted methods of solving a system of inequalities do not distinguish between the different elements in the variable space which satisfy the constraints to a different degree, whereas in practice it is relevant to know how many important constraints each region in the variable space satisfies and to what degree. Finally, the common solution methods for systems of inequalities produce a sharp constraint, whereas in many practical problems a fuzzy constraint provides a better reflection of the uncertainty of the described situation.

As a compromise, we proposed (Sher, 1978) the use of non-point object estimates in the form of domains of n-dimensional space defined by inequality systems. Object representation as a domain is more informa- tive than point representation because, together with estimation of the object, it characterizes its degree of indeterminacy.

(8)

428 Arnold Sher, Ilan Amir

usual sense) is solved by using a linear form, instead of the minimax consistency principle for inequalities. This approach is a generalization of the classical concepts, designed to eliminate the above-mentioned restrictions.

The definition, proposed by Sher (1980), is applied to form fuzzy constraints from the initial sharp constraints specified by systems of two- sided inequalities. The mathematical programming problem with a linear function is solved in the fuzzy constraints constructed from these systems of inequalities.

Consider the system of inequalities

Gj(x) < 0, j = 1,2 . . . . , m; x ~ (Xl, x 2 , . . . ,Xn) E R" (6)

and the vector of weight coefficient A - {hj}~'=l normalized by the condi- tion

m

E Aj=I, r a g > 0 j = l

Definition 1. A fuzzy solution of the system (6) for a given weight vector A is the fuzzy set

FA - {(x, /ZA(X)) I /ZA(X) > 0} where

m

A(x) = Z Aj+j(x)

j=l with

1, ifGy(x) < 0

~oj(x) = 0, otherwise

(7)

Here /ZA(X) e [0,1] is interpreted as the degree to which the element x e R" satisfies the given system (6); the coefficient A/is interpreted as a quantitative measure of importance (necessity) of the inequality Gs(x ) < 0 in the system (6), FA is interpreted as a fuzzy constraint in the space R".

Moreover, the scalar a e [0,1].

Definition 2. A (a, A) solution of the system (6) is the fuzzy set

F~ -= {(x, /ZA(X)) I ]£A(x) -> a}

This definition is a generalization of the classical (minimax) definition, to which it is reduced for a = 1. The vector A does not enter the classical solution.

(9)

l = 1,2 . . . . , L~, where L~ < m, if Vj: A/= 1/m, and L~ < 2 m for an arbi- trary relation between Aj, j = 1,2, . . . , m.

Let Et - {x I /ZA(X) = const = /31 --- a} and ~A(Et) -/31. Then the following definition is equivalent to the preceding.

Definition 2a. A (a, A) solution of the system (6) is the fuzzy set

L a

=

By varying the parameters a and A, we generate a continuous set of consistency principles for the inequalities in (6). This set includes the classical relation consistency principles (Luce & Raiffa, 1957; Mirkin, 1974), which are thus special cases of (a, A) solutions. For example, the majority principle corresponds to a > 0.5, aj > 0, j = 1,2, . . . , m; the simple majority principle to a > 0.5, A/= l/m, j = 1, 2 . . . m; the minimax principle (the classical solution of the system (6)) to a = 1, A j , 0, j = 1,2 . . . m, and the dictatorial principle to a * 0 for o n e j (aj = 0 for all other j).

N o w consider an objective function ~(x).

Definition 3. A (a, A) solution of the mathematical programming prob-

lem with fuzzy constraints F~A is the fuzzy set

<I:'~A - {(2 I, /XA(.~) I 21 e -=1, ~(21) = max ~(x), /./,A(X) ~ Ot}~_- 1.

X E ~'1

This definition is a generalization of the mathematical programming problem with unfuzzy constraints, to which it reduces for a = 1. The vector A is not used in the conventional formulation. O~ is the set of vectors ~ on which the objective function W(x) attains its maximum in the corresponding region ~,l, each of these vectors satisfying the system of constraints (6) to a certain degree/XA(:~ a) ~ [0, 1]"

It has been shown (Sher, 1982) that the solving of a mathematical programming problem with fuzzy constraints, which are the result of a fuzzy solution of a system of m inequalities in n-dimensional space, is reduced to a solving of 2 mn mathematical programming problems with unfuzzy constraints. The necessity to solve such a large number of problems makes the development of special methods and algorithm reasonable.

Concordance of two-sided inequality system

Problem formulation

(10)

This descriptive problem can be formulated as follows. The following are given:

(a) a system of m subsystems, each of two-sided inequalities (see Table 2)

( ( a l l <-- X l < bll "~ (a2, <- Xl < b2,'~ ~lml <-- X1 < bml'~ "~ ... " , . . . , ~ . m 2 < - x 2 < b m 2 ~

l

.....................

< . . .

~ ~lln <-- X n < bl n ,] ka2n < Xn <

b2~]

la,,m

<-- X n <

b,,~JJ

or in more compact notation

{{aji < xi < bfi}7:l}7=l (8)

(b) a vector of weight coefficients in equalities (in our problem Aj is a probability o f j t h rainfall)

m A = { / ~ j } j = l ,

(c) a scalar a ~ [0,1] (d) values of rainfall {ry}jml

m

Aj=I, Vj: Aj~O

j = l

(e) objective function coefficients

{{~/zj}j=l

}7=1 are the net of ith crop for the j t h amount of rainfall

(f) a factor K ~ [0,1] that converts gross income to net income. Find the fuzzy set

F ~ : {(0t,/XA(0,), r(Ot), {T,(Ot)~=l)l & Pk, k = 1,2 . . . 5}

where & denotes intersection (simultaneous truth) of the conditions Pk,

which are defined as follows

PI: x = (x 1, x2,..., Xn) e Rn; x; is the area of t h e / t h crop

m

Pl: /XA(X) = ~ A/%(x)--the function meeting initial constraints and j=l expressing the probability of rainfall r(x)

m

r(x) = ]L rjAj%(x)/i.,A(x)--rainfall function

j=l

m

Vi = 1, n: %(x) = K 2~ %Aj%(x)/I.ZA(X) coefficients of the objective

j=l function at point x

q~j(x)={~' otherwiseifVi=l'n:aji<xt<bji

P3: Ot = {x [ /zA(X) = const}

P4: /l"A(0t) = ~A(X), r(Ot) = r(x), Vi = 1, n: %(Ot) = T,(x) I x ~ O,

(11)

Since x is defined in a continuous space R", the computation of functions/~(x),

r(x),

y,(x) in all points x is impossible, as such an algorithm would be endless.

The suggested solution makes use of the fact that functions ~(x),

r(x),

y,(x) are piecewise-constant. Then the problem is to reduce to the description of all the domains, within the limits of which functions ~(x),

r(x),

y,(x) do not change their values. Since the number of such domains is finite, the solving algorithm is finite too.

The method of construction of fuzzy constraints is described in the Appendix.

Optimization o f a linear function on a fuzzy set obtained from a two-sided inequality system

Problem formulation

The problem of optimization of a function with fuzzy constraints can be stated as follows:

Consider a fuzzy set

Or} t =1 F~A {(0,, ~.i,A(0t))l ~[,A(0t) ~> Tot

which defines the corresponding finite set B ={/3t}~=1 of the function /XA(0/), t = 1, 2, . . . ,Tot; the objective function is linear

q'(x) = ~ 3'~i

i=1

t Tot Tot

and the vectors {F } t =1 = {{ ~}7=1 }t=l of non-negative coefficients y[ of the objective function on each hyperparallelepiped

Ot,

v e c t o r {r(Ot)}Ta-_l and the constant C.

Find the fuzzy set of maxima

~ = {(~,/~A(-~F), ~F(£'t), r(:~'))I &Pk, k = 6, 7 . . . . ,10}~=1

where

p6: x = (Xl, x2, . . . , x , ) ~ R"

m: =-t = {x l u, n(x) = 13~}

P8: Yd ~ Et

P9: ~(X") = max ~(x)

r(~;-') = r(O~) ] t = arg(.~ ~ O, , c ~-t)

Plo: ~ ~ < C

(12)

TABLE 3

Results for Planning with Fuzzy Constraints

r(.~ txA(.~ ~ ( ~ :¢t = (~, :et2 .. . . : e t ) Coefficients of the Rainfall Proba- Objective Area of crops (ha) objective function (S/ha)

(mm) bility function ($)

1 388 0-630 6455 22 19 16 19 24 122 45 30 96 25

2 458 0-520 7 922 32 19 12 20 17 130 46 32 103 26 3 455 0.430 7 212 28 19 17 19 17 125 46 31 100 25

4 417 0.360 7 324 32 10 20 20 17 121 44 31 98 25

5 324 0.310 5 565 21 19 17 19 24 107 40 26 82 23 6 470 0.200 7 108 32 20 20 20 20 120 40 28 92 24

7 228 0.180 3 029 21 0 0 19 60 58 17 19 26 22

8 150 0-040 1 300 0 0 0 0 100 0 0 0 0 13

The algorithm, for optimization of a linear objective function on a fuzzy constraints which are the result of intersection of fuzzy solution of two-sided inequality system and linear constraints, is presented in the Appendix.

RESULTS

Results of the application of the fuzzy set method, using the optimal solutions and the ranges of insensitivity, are presented in Table 3. Table 3 reads: for a (weighted) rainfall amount of 388 mm, there is a probability of 63% that the net income will be $6455. For this case the areas of the crops will be: ~l---cotton -- 22 ha: ~2--wheat = 19 ha; ~3--barley = 16 ha; ~4---chick-pea = 19 ha; and ~5--oats = 24 ha (total area of crops is C = 100) and linear objective function coefficients are: for c o t t o n - - 122 S/ha, for wheat--45 S/ha, for barley--30 S/ha, for c h i c k - p e a - 96 S/ha, for oat--25 S/ha. For brevity, in Table 3, coefficients are presented with accuracy of integers. It is important to note that they vary in different areas of crops.

DISCUSSION

[image:12.468.60.408.83.273.2]

(13)

To evaluate LPFC, plans of the unirrigated farm resulting from LP and LPFC have been compared.

Regarding the regular LP, the limits of insensitivity calculated by POSA, although available as information to the decision maker, have not been included and thus not considered, in the decision-making process. The most one can expect from the data of LP is the optimal solutions (Table 2), as a basis for calculation of the expected values of the objective function under various rainfall amounts. These expected values are calculated by the following procedure: for a selected rainfall amount j, the optimal plan, calculated by LP, provides the value of the objective

function Zj* and the vector of the optimal decision variables x*

Z*= K ~ Yijx~ (9)

J

where K is the factor that converts gross income to net income (in our case K = 0.3). The factor K is used for both (LP and LPFC) plans. For each selected plan the expected value of the income from corresponding crop is determined by multiplying the value of the objective function Zj* by the probability of rainfall, )tj

Zj ---- ¢~jZ?

(lO)

For example, let us calculate the expected value of net income for r 3 = 450 mm. From Table 2, the probability of r 3 = 450 mm is hj -- 0.32 and the optimal plan is: x~ = 32; x2 = 0; x3 = 20; x4 = 20; and x 5 = 3.33 ha. From this plan the value of the objective function is calculated by eqn (9) for Z~ ( r 3 = 450 mm)

ZJ': 0-3*(454*32 + 165.0 + 115.20 + 368*20 + 90*3.33)

= 0.3*24488--- $7346

The expected value of net income for the plan under r 3 = 450 m m with probability h 3 = 0.32, from eqn (10), is E(Z3*) = $7346*0-32 = $2351.

The values of the objective function and the expected values of net income for the various amounts of rainfall are presented in Table 4. As explained earlier, Table 4 can be considered as the best data available to the decision maker provided by LP without fuzzy constraints.

The evaluation of LPFC can be made by comparing its plans (Table 3) with the plans of the regular LP in Table 4.

(14)

TABLE 4

Values of the Objective Function and Expected Values of Net Income for Various Probabilities of Rainfall, by regular LP Methods

j 1 2 3 4 5 6

Probability Aj 0-07 0.16 0.32 0.27 0.14 0.04

Value of objective 7 602 8 265 7 346 6 298 3 627 1 290

function Z7($)

Expected value of net 532 1 322 2 351 1 700 508 52

income E(Z*)($)

the sense that within these ranges the optimal basis is not changed, (eqns (2) and (3) as has been explained earlier). The sum of probabilities of Table 4, however, is 100%, because the plan, and its value of objective function, is valid for a certain amount of rainfall under a certain probability of occurrence.

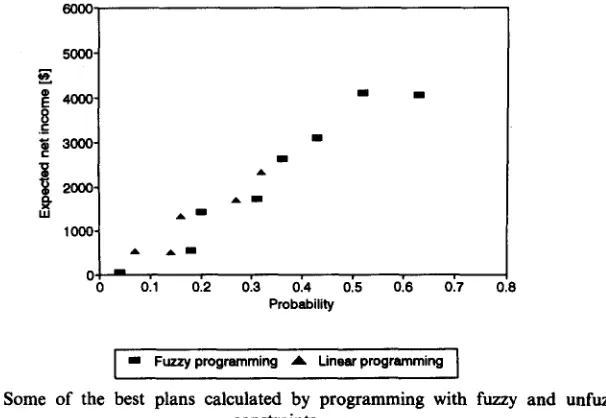
Figure 1 shows the expected net income for different plans, calculated by LP on the basis of Table 4 and eqn (10), and the expected income for plans calculated by LPFC with data in Table 3 used the following equation

Figure 1 clearly shows that the expected values of four plans resulting from the suggested method are higher than all plans resulting from regu-

6000-

5000-

~= 4000-

8

.c "~ 3OOO-

f -

LU

1000.

o l

A I I I

I I

A I

A A I

l

o11 o12 o:3 o:4 ols o18 o:7 0.6

Probability

Fig. 1.

" Fuzzy programming ~ Unearprogr~'nming I

[image:14.468.61.409.92.216.2] [image:14.468.92.395.416.625.2]

(15)

lar LP. Since the expected value of a plan is one of the most important factors for decision making under uncertainty and since the expected value of LPFC are significantly higher than those of LP, we may evaluate the suggested method as a better method than the regular LP.

The improvement made by the LPFC method can be explained by the fact that it uses the LP output as a basis and adds to it more elements that improve the available information and reduces the uncertainty of the resulting outcome. This is done without requiring additional data from the planned system.

CONCLUSIONS

In this work the LPFC method is introduced to improve decision making in agricultural systems operated under severe uncertainty. The LPFC method has been compared to a regular LP method that is very commonly used for planning these systems. The comparison was applied to a simple but typical system--an unirrigated farm that is dependent on un- certain rainfalls. From the presentation and the resulting plans of both methods, it is quite evident that the LPFC method has a significant advantage over the regular LP because it allows reducing the uncertainty while using the same data.

The example in this paper, however should be followed by other, more complicated applications for evaluation of the LPFC method.

The concepts described make up a fuzzy solution of a system of two-sided inequalities and a solution of the mathematical programming problem with a linear objective function and fuzzy constraints. Construc- tive methods were proposed for fuzzy set selection through concordance of expert estimates represented as domains in n-dimensional space described by non-equivalence of general inequalities and through objective functions optimization under fuzzy constraints.

The fuzzy decision of an inequality system is a generalization of the commonly used decision (as the decision intersection for every inequality belonging to the system), and it enables us to take into account the different importance of the inequality subsystem by means of the weighting coefficient vector and to solve the incompatible (in the usual sense) inequality system.

(16)

436 Arnold Sher, llan Amir

tion of the objective function on the continued fuzzy set to a finite set of optimization problems in non-fuzzy constraints followed by the development of a fuzzy set of objective function optima.

The introduction of fuzzy constraints into the optimization gives it some peculiarities in contrast to the classical problem of mathematical programming under non-fuzzy constraints. The objective function optimization under fuzzy constraints is, primarily, a generalization of the mathematical programming problem. The solution of the mathematical programming problem is practically final and may be directly used (e.g. for planning). Optimization under fuzzy constraints is not final and may be regarded as source data for subsequent optimization problems.

There is no problem of solution concordance in the mathematical programming problem with unfuzzy constraints: a solution is either unique, or solutions have identical optima (then, any of them is selected), or there is no solution at all. The completion of optimization under fuzzy constraints gives rise to another problem, namely, that of concordance of its solution set. A particular form of concordance is defined by the solution objective, for instance, by the requirement that optimal selection be made by alternatives leading to a certain value of objective function and satisfying to a certain extent initial constraints, thus leading to the formal formulation of the vector (multicriteria) optimization problem.

These methods may be used for solving the problems of planning and control under vagueness conditions and for studying their stability. They are also used for decision-making problems based on the non-point expert estimations, which are specified in terms of regions in multidimensional space by means of the inequality systems and for the parameter optimization problems of designed technical systems, if the set of incompatible and contradictory requirements exists.

REFERENCES

Amir, I., Shamir, U. & Broughton, R. S. (1978). Monitoring and decision making processes for operating agricultural production systems. Agric. Systems,

3. 253-64.

Amir, I., Puech, J. & Granier, J. (1991). ISFARM: An integrated system for farm management: Part 1--Methodology. Agric Systems, 35, 455-69. Amir, I., Puech, J. & Granier, J. (1993). ISFARM: Part 2--Applicability. Agric.

Systems, 41, 23-39.

Charnes, A. & Cooper, W. W. (1963). Deterministic equivalents for optimizing and satisfying under chance-constraints. Operations Research, Vol. II, pp. 18-39.

(17)

Gui, X. O. & Goering, C. E. (1990). Introduction to fuzzy set theory and applications. Trans. ASAE, 33(1), 306-13.

Luce, R. D. & Raiffa, H. (1957). Games and Decision. Wiley, New York. Mirkin, B. G. (1974). Group Choice. Novosibirsk: Nauka, 256 pp. (in Russian). Sher, A. P. (1978). Concordance of non-point expert estimates and the member-

ship function in the fuzzy set method. Simulation and research of automatic control systems. Vladivostok, pp. 111-18 (in Russian).

Sher, A. P. (1980). Solution of the mathematical programming problem with a linear objective function and fuzzy constraints. Avtomatika i Telemekhanika, 7, 137--43 (in Russian).

Sher, A. P. (1982). Algorithmic methods for fuzzy set selection via non-point expert estimates. Problems o f Control and Information Theory, vol. 1 l, No l, pp. 41-52 (in Russian).

Thangavadivelu, S. & Colvin, T. S. (1991). Tratiicability determination using fuzzy set theory. Trans. ASAE, 34(5), 2272-8.

Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8, 338-53.

A P P E N D I X

Construction of fuzzy constraints

N o w we describe the m e t h o d o f solving this problem. Step 1. Set i = 1.

Step 2. F o r m the sequence

Ei = {ezi, ez+l.il ezi = ajt, ez+l.i = bji;j = 1,2 . . . m; z = 1,3 . . . . , 2m - 1}. Step 3. O r d e r the sequence E~ so that the successive terms are non- decreasing. We obtain the non-decreasing sequence

E;' = {ek~ I Vk: ek; -< ek+l,i; k = l, 2 , . . . , 2m - 1 }.

Step 4. R e m o v e f r o m E;' difference occurrences o f identical terms, leav- ing only one representative o f each group. We obtain the increasing sequence

Ei" = {eki I Vk'. eki < ek+l,i; k = 1, 2 . . . . , m i - 1; mi < 2m}. Step 5. F o r m the adjacent elements o f E~" into two-sided inequalities

{Pki <- Xi < qki [ Pki = eki; qki = ek+l,i}~i=l 1

Step 6. Set i = i + 1 and go back to Step 2 if i < n. O n exiting the loop in i, we have the set o f two-sided inequalities

(18)

438 ArnoM Sher, Ilan Amir

n u m b e r o f two-sided inequalities: m; - 1, for difference i. T h e total n u m b e r N o f the two-sided inequalities is given by

rl

N = ~ (m, - 1)

i=1

Let 02 be a c o m b i n a t i o n o f n f r o m N inequalities in (11), n

02 ={Pzi < xi < qzi}7=l, z = 1, 2 . . . Q = I-I(mi - 1)

i=1

where every Oz contains inequalities with a given index i only once.

Step 7. F o r m { 0~}, z = 1, 2 . . . Q.

Step 8. Set z = 1.

Step 9. Set j = 1.

Step 10. C o m p u t e

= : 1, if Vi: [Pz,, qz,) n [aj,, bj,) ~ 0

Oz)

t 0 otherwise

Step 11. S e t j = j + 1 a n d return to Step 10 if j < m.

m

]£A(Oz) --- X )~j~oj(Oz) j= I

r( Oz) = o__)

j=l

m

Vi = 1, n: 7;(0z) = K ~ 70.Aj%(O:)/tXA(O_-)

j = l

Step 13. Set z = z + 1 a n d return to Step 9 if z < Q. O n exiting the

loop in z, we have the set

F A = {(Oz, /ZA(0z), r(Oz), {'Y,(Oz)}n=l)}Qz=l

Step 14. F o r m

F ~ - - ~A\{(0z, ~t/~A(0z) , r(Oz) , {7,(Oz)}7=O l i~A(Oz) < a}

We have

0 n Ta

F ~ = {(Ot, /tA(Ot), r(Ot), {Y,( t)}~=0 I /.*A(0,) --> Ot},=l, T a < Q

(19)

Algorithm for optimization of a linear

objective

function on fuzzy constraints

N o w we present an algorithm for solving this problem.

Step 15. D e t e r m i n e the n u m b e r L~ a n d f o r m the sequence {/3t}t~_-I o f

different values/3 t o f the function/ZA(0t) on all Ot c 1~ ~A.

Step 16. Set t = 1.

T h e following action will find a p o i n t __x t ~ Or, satisfying

so that

< c,

i=I

~(x_') = m a x ~ ( x ) x ~ 0~, ~'~ = j x~ -< C

T o m a k e the e n u m e r a t i o n in x as goal-directed as possible, we recall that the m a x i m u m o f a linear objective function with non-negative coefficients o n the hyperparallelepiped Ot with the constraint Ex~ < C is attained at the p o i n t o f intersection o f its edge a n d h y p e r p l a n e ~;c~ = C. Therefore, to find m a x ff'(x) on 0t, it is e n o u g h to determine the values o f • (x) at the points o f intersection o f 0t a n d Z.x~ = C a n d select the largest. T o solve this problem, we first have to construct the vectors, which are the points of intersection o f the hyperparallelepiped Ot edges a n d hyperplane Ex; = C.

H

Step 17. If ~ Pti >C t h e n go to Step 27.

i=1 H

Step 18. If ~ qa < C then c o m p u t e

i=1

n

x---t IX--- t = {qti}in=l; air(X-- t) = ~ "Y,qti

i=1

a n d go to Step 27.

Step 19. Set ~t'(_x_ t) = 0 - - t h e initial value o f the objective function in the

hyperparallelepiped Or

Step 20. Set i = 1.

Step 21. Set k = 1.

Step 22. Set VI = 1, n: xt = Pa.

Step 23. If i ~: k then c o m p u t e

8 = C - _Ptt

(20)

440 Arnold Sher, Ilan Amir

xi = min (6, qt3 A = 6 - qa

Xk = min (q,i, m a x (Ptk, Ptk +A))

We have the vector x = (Xl, x2 . . . x,) which contains the coordinates o f intersection between an edge o f the hyperparallelepiped Ot and hyperplane Y.xi = C.

n

Step 24. If W(x_ t) < 2~ ~ x i then set

i=1

q'(x') < xi; x_' = x 2 , . . . , x , ) .

i=1

Step 25. Set k = k + 1 and return to Step 22 if k < n.

Step 26. Set i = i + 1 and return Step 21 if i < n. Exiting the loop in i,

we have a value o f an objective function m a x i m u m and its coordinates in the hyperparallelepiped 0,.

Step 27. Set t = t + 1 and return to Step 17 if t < T~. On exiting the

loop in t, we have the set

{ x t l W ( x ~) = max ~t'(x)}

x~ o,.y_.xi<_c

Step 28. Set l = 1.

Step 29. Find the n u m b e r Ht o f Ot so that/~A(03 = /3t a n d f o r m the set

E I : {Oh I ]£A(Oh) : ~l}lffl__l

N o t e that in general the set ~-t is neither convex n o r simply connected.

~ i I ~1 ~ ~1, q~(~l) = m a x W(_x h)

The problem o f optimization in a nonconvex, multiple-connected re- # o n ~ / i s thus reduced to finding the optimal solution on a finite set (with cardinality Ht) o f optimization problems on convex and simply connected regions Oh which are the c o m p o n e n t s o f ~t.

C o m p u t e

r(Et) = r ( ~ t) = r(Oh) I h = arg (~t ~ Oh C ~1)

Step 31. Set/~A(~ t) = /3t

Step 32. Set l = l + 1 a n d return to Step 29 if l < L~. O n exiting the

(21)

Optimization with fuzzy constraints in production planning 441

The problem of optimization with fuzzy constraints " " / a

F~ = {(-=1, /zA(=t))}t--1