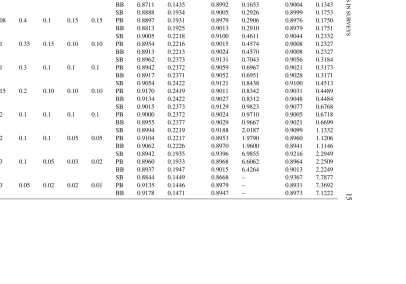
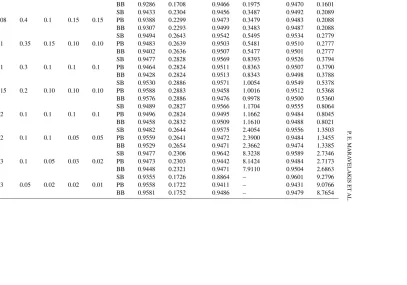
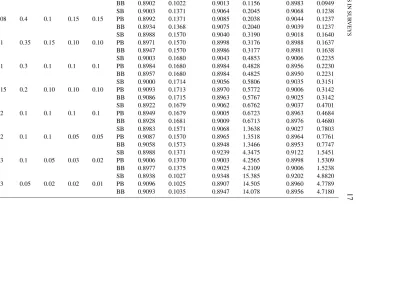
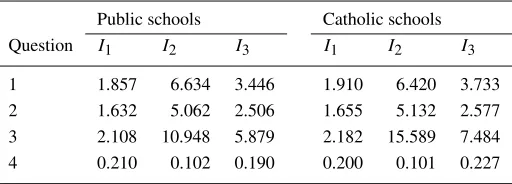
The Use of Indices in Surveys
Full text
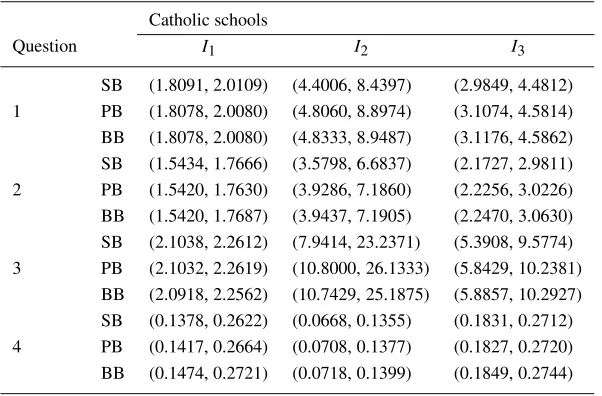
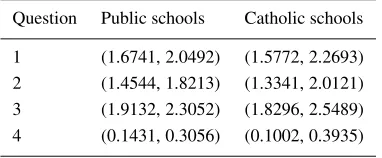
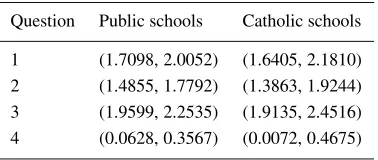
Figure
Related documents
We provide a comprehensive range of pooled products across fixed income, equities, multi- asset, absolute return, real estate, liquidity and private equity.. In particular, we
The methodology for the automatic detection and monitoring of plumes caused by major technological accidents on NOAA/AVHRR (Advanced Very High Resolution Radiometer) imagery, uses
Representative corneal topogra- phies from sequential Pentacam examinations are shown in a 29-year-old patient from the simultaneous group (same-day, simultaneous
For gas boilers, paragraph 2.14 states that we are required to obtain a declaration from the customer confirming they did not pay a fee for the warranty, whereas for electric storage
This capstone will present a physical science unit that incorporates concepts from a content-based instruction (CBI) curriculum as well as inquiry-based learning (IBL) curriculum
Such forward-looking statements are based on numerous assumptions regarding the Bank’s present and future business strategies and the environment in which the Bank will operate in
A period of 2 months after cessation of overuse is stipulated in which improvement (resolution of headache, or reversion to its previous pattern) must occur if the diagnosis is to
We investigated risks of leukemia (10 th revision of the International Classification of Disease, C91-C95), brain/central nervous system cancers (C70-C72), malignant melanoma