Two-party Private Set Intersection with an Untrusted Third Party
Full text
Figure




Related documents
Red dashed line represents sugar release under pretreatment at 190°C for 10 minutes (43.0%).. robustness of techno-economic models [36]. Assuming that enzyme loading is a key barrier
Figure 14: Evolution, for one image of the Corel database, of the 14 studied criteria for segmentation results obtained with the Canny filter using di ff erent thresholds.. Figure
While the specificity of the Chinese context—and food safety concerns related to infant formula in particular—is important to understanding new emphasis upon breastfeeding in
The converse of the above proposition need not be true in general as seen in the following example.. The converse of the above proposition is not true which is proved in the
This data element may contain the same information as ''Provider location address telephone number''.. Provider Business Mailing Address
This paper is structured in four sections: first, it presents the methods used to review the available literature; second, it examines the relevance of making
These observations hint at a mutually repressive relationship between Gata6 and Nanog and it is thought that early co- expression of the factors is maintained
Avidities using binding interference or elution with a single dilution of the chaotrope and serial dilutions of the serum sample were expressed in terms of the percent reduction in

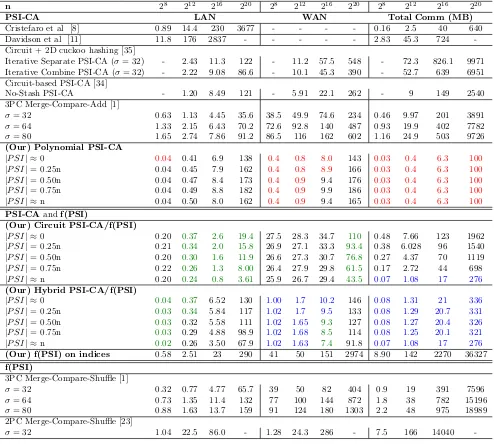

![Table 5: Runtime in seconds in LAN/WAN setting and communication cost in megabytes. In [38], the communi-cation cost does not include the cost to perform base OT](https://thumb-us.123doks.com/thumbv2/123dok_us/7991386.1326442/25.612.62.549.98.332/runtime-seconds-setting-communication-megabytes-communi-include-perform.webp)