Lightweight Design Choices for
LED
-like Block
Ciphers
Sumanta Sarkar1, Habeeb Syed1, and Rajat Sadhukhan2 and Debdeep Mukhopadhyay2
1 TCS Innovation Labs, Hyderabad, INDIA
sumanta.sarkar1@tcs.com, habeeb.syed@tcs.com
2 Indian Institute of Technology, Kharagpur, INDIA
rajatssr835@gmail.com, debdeep.mukhopadhyay@gmail.com
Abstract. Serial matrices are a preferred choice for building diffusion layers of lightweight block ciphers as one just needs to implement the last row of such a matrix. In this work we analyze a new class of serial matrices which are the lightest possible 4×4 serial matrix that can be used to build diffusion layers. With this new matrix we show that block ciphers likeLEDcan be implemented with a reduced area in hardware de-signs, though it has to be cycled for more iterations. Further, we suggest the usage of an alternative S-box to the standard S-box used inLEDwith similar cryptographic robustness, albeit having lesser area footprint. Fi-nally, we combine these ideas in an end-end FPGA based prototype of
LED. We show that with these optimizations, there is a reduction of 16% in area footprint of one round implementation ofLED.
Keywords: MDS matrix, Serial matrix, Recursive Diffusion Layer, Lightweight, S-box,LED.
1
Introduction
Lightweight Cryptography is an area that is focused on research and development of cryptographic algorithms suitable for resource constrained devices like RFID tags, wireless sensors, etc. These kind of devices have very low resource, and as such the usual cryptographic algorithms likeAES, RSA etc. are not suitable therein. Internet of Things (IoT) is a network of devices like RFIDs/sensors. Therefore, lightweight cryptography plays a crucial role in securing the data that flows in IoT network. IoT has wide applications, for example, health monitoring, supply chain, defense, etc. Thus low area footprint and high throughput are two key areas of focus in lightweight cryptography. Some known lightweight block ciphers includePRESENT[3],PRINCE[4],CLEFIA[20].
satisfy the condition that its every possible square sub matrix has to be non singular. This requirement makes it challenging to find MDS matrices having efficient implementation in hardware.
In [11] the metric XOR count that measures the implementation cost of a dif-fusion matrix is introduced. Using this metric one can find MDS matrices which can be efficiently implemented in resource constrained environment. In the re-cent document produced by NIST [14], the requirement of simpler rounds as a lightweight design principle was emphasized wherein a simple round is iterated over multiple cycles to achieve the desired security. This idea popularized by the lightweight hash function, PHOTON [6] and block cipher,LED[7]. However, it is an open research problem of striving to find further lightweight construc-tions which can be iterated multiple times to obtain the desired security levels. This method provides an effective mechanism of obtaining lightweight imple-mentations, while not compromising on security, albeit at the cost of extra clock cycles. While for lightweight applications, the gate count of the design is of ut-most priority, which can be achieved at the penalty of extra clock cycles, in some applications it may be also a constraint to ensure that the latency does not blow up significantly. This may be important specifically in those environments where energy is also of utmost importance. Hence, it is an interesting research problem of finding lightweight primitives, like linear layers, S-boxes, which can be iter-ated or cascaded to obtain the same security. On the other hand, the architecture should also amortize the extra latency by employing suitable techniques, which we also strive to find in this work.
re-quirement of the other lightweight features like throughput, energy, etc, depends on the applications. For example, if we consider environment monitoring as an IoT application, then we can afford some latency in the encryption algorithm, as this application does not require immediate action upon receiving the data from the environment. However, as the devices are low resourced, it becomes important to decrease the area footprint as low as possible.
Rest of the paper is organized as follows: in Section 2 we recall some intro-ductory results on serial matrices, XOR counts followed by Section 3 in which we present some new recursive MDS matrices defined by extremely lightweight serial matrices. In Section 4 we describe details of implementation of or new primitives inLEDblock cipher and the resulting optimizations.
2
Preliminaries
Here we briefly recall some basic facts about linear diffusion layers and MDS matrices. Denote byF2m finite field of size 2m. For anyx= (x0, . . . , xn−1)∈Fn2m itsm-weightwtm(x) (or simply wt(x) when there no ambiguity) is the count of non zero elements in x. An n×n linear diffusion layer over m-bit words is a linear map T : Fn2m −→ Fn2m. Diffusion property ofT is measured in terms of
differential branch number, which is defined as
BN(T) = min x∈Fn2m,x6=0
{wt(x) +wt(T x)}.
It is well known [5, Ch 9] thatBN(T)≤n+ 1 and a diffusion layer that attains the maximum is known as perfect diffusion layer?. Linear diffusion layers are closely connected with MDS codes. LetC= [2n, n] be a linear code defined over
F2m. Suppose that [I|C] is a generator matrix of C, where I is n×n identity matrix and C is a non singular matrix of the same size. Such a code is MDS if the minimum distance of the code attains Singleton bound [13], i.e., if the minimum distance is 2n−n+ 1 =n+ 1. Note that the matrixC can be used to define ann×nlinear diffusion layer overF2m and the codeC is MDS if and only ifBN(C) =n+ 1. Extending the notion of MDS codes to matrices, we say that the matrix C is MDS if the code C is MDS. Another independent way of characterizing an MDS matrix is given below which we will be using to check if a given square matrix is MDS:
Fact 1 [13, Ch.4] Ann×n matrix M overF2m is MDS if and only if every square submatrix ofM is nonsingular.
2.1 XOR Counts
The finite field F2m is also a m dimensional vector space over F2. This vec-tor space has several bases but we use only the polynomial basis given by
?The term “perfect diffusion layer” was coined by Vaudenay in [22] wherein he
{α, α2, . . . , αm−1
} where α is the root of the irreducible polynomial that de-fines F2m over F2. The notion of XOR count defined below, was introduced in [11] to measure the cost of field multiplication in F2m.
Definition 1. Let B be a vector space basis ofF2m over F2. For any a∈F2m
the XOR count of a with respect toB is denoted byXOR (a)and is defined as the number of XORs needed to implement the field multiplication of a with an arbitrary element b∈F2m
Though the XOR count ofadepends on basis ofF2m, we simply denote it by XOR (a) whenever there is no ambiguity. Using this metric one can find diffusion matrices which can be efficiently implemented.
The linear diffusion layers in block ciphers are defined by MDS matrices. In [11] the notion of XOR count of an element was extended to XOR count of a row of a matrix. SupposeRi is a rowRi = (βi,0, . . . , βi,n−1)∈Fn2m of a matrix. Denote by ρi the number of non zero entries in Ri, then the XOR s needed to implement rowRi is given by
n−1
X
j=0
XOR (βi,j) + (ρi−1)·m. (1)
This notion of XOR count was further extended to the full matrix in [18] as
XOR (M) = n
X
i=0 n−1
X
j=0
XOR (βi,j) + n
X
i=0
(ρi−1)·m, (2)
where M is an n×nmatrix over F2m. In this paper we are mainly focused on Serial matrices, in which we only need to know the cost of the last row (1).
Based on the notion of XOR count several works followed [12,17,21] in order to obtain MDS matrices with low XOR counts. For instance, [18] showed the minimum value of XOR count that 4×4 MDS matrices can have overF24 and
F28. Recently [19] presented 8×8 MDS MDS matrices with the lowest known XOR counts overF24 andF28.
3
Recursive MDS Matrices
A serial matrix of ordern×noverF2m is a matrix of the form
S =
0 1 . . . 0 0 0 . . . 0 ..
. ... . . . ... 0 0 . . . 1 a0a1. . . an−1
which is usually denoted by S = Serial (a0, . . . , an−1). The matrix S is companion matrix of the monic polynomiala0+a1X+. . .+an−1Xn−1+Xn∈F2m[X] with a06= 0. One can easily see that inverse of S is
S−1 =
a1 a0
a2 a0 . . .
an−1 a0
1 a0 1 0 . . . 0 0 0 1 . . . 0 0
..
. ... . . . ... 0 0 . . . 1 0
. (4)
By a recursive MDS matrix we mean a MDS matrix M such that M = Si for some serial matrix S and positive integer i. Recursive MDS matrices are a preferred choice for diffusion layers in lightweight cryptography as only the last row of such a matrix needs to be implemented. However, the downside is that it causes latency since the output of diffusion layer is obtained by applying S recursively as
(y0, . . . , yn−1) = S. . .(S
| {z }
itimes
(x0, . . . , xn−1)). . .). (5)
An additional advantage of using recursive MDS matrix in block cipher is that its inverse also has simple form (as in (4)) and can be implemented efficiently.
Several techniques have been proposed to construct recursive diffusion layers. In [1, 16, 23] authors presented construction of recursive diffusion layers using binary linear maps instead of matrices defined overF2m. Later Augot and Finiasz constructed recursive MDS matrices from shortened BCH codes [2] following which more general characterization of Recursive MDS matrices is presented in [8,9]. In [10] authors discussed construction of 4×4 MDS matrices from serial matrices defined over sets of the form{1, α, α2, α+ 1
} ⊂F2m.
3.1 Lightweight Recursive MDS Matrices
If S = Serial (a0, . . . , an−1) is an n×n serial matrix defined over F2m then it is easy to see that the least possible value of i for which Si is MDS is i = n. Consequently while constructing such MDS matrices the usual practice is to find an n×n serial matrices S for which Sn is MDS. This is done mainly to minimize throughput latency: If Siis MDS then we neediiterations to compute the outputy= (Si)
·x(see (5)) and hence optimal throughput is achieved when i=n.However, it is possible to find new lightweight serial matrices S such that Si is MDS if we assumei
≥n.
S =
0 1 . . . 0 0 0 . . . 0
..
. ... . . . ... 0 0 . . . 1 a0a1. . . an−1
= X X2 .. . Xn−1 Xnmodf(X)
| {z }
(∗)
(6)
where elements of each row in the matrix (∗) consists of coefficients of the poly-nomial given in that row. With these notations it is easy to see that for any i≥1 the matrix Si is given by
Si =
Ximodf(X) Xi+1modf(X)
.. .
Xi+(n−1)modf(X)
. (7)
Recall that in general one is interested inn×n serial matrices S for which Sn is MDS in order to optimize the throughput. However in many cases it is not possible to obtain such MDS matrices. In the following we identify two such classes.
Lemma 1. Let n≥4 andS = Serial (a0, . . . , an−1),be defined overF2m. Then Sn is notMDS if a
n−1=an−2= 1 oran−1=an−3= 1.
Proof. Supposef(X) =a0+. . .+an−1Xn−1+Xn be the the polynomial
asso-ciated with the matrix S.We definec, cias follows. Letc=a2n−1+an−2and for i= 0, . . . , n−3,
ci=ai·an−1+ai−1, (8)
where we use the convention that ai = 0 fori < 0. Using these notations one can check that
Xn+2modf(X) =a0 ·c +
n−2
X
i=1
(aic+ci−1)Xi+ (an3−1+an−3)Xn−1. (9)
From (7) it follows that the coefficients occurring in above polynomial form third row in the matrix Sn. If a
n−1 = an−2 = 1 then we get that c = 0 and consequently the matrix Sn is not MDS. Similarly ifa
n−1=an−3= 1 then the coefficient ofXn−1 in (9) becomes zero and the matrix Sn is not MDS.
u t
Lemma 2. LetS = Serial (a0, . . . , an−1)be a matrix defined overF2m. ThenSn
is not MDSif ai−1=ai=an−1= 1 for anyi= 1, . . . , n−2
Proof. Usingci as in (8) we have
Xn+1modf(X) =a0an−1+ n−2
X
i=1
coefficients of which occur as second row in the matrix Sn. Here we have defined cn−2 precisely as in (8). Ifai−1 =ai =an−1= 1 for any i= 1, . . . , n−2 then
ci= 0 and hence the matrix Sn is not MDS. ut
While searching for lightweight recursive MDS matrices one would like to con-sider the lightest possible serial matrix, S = Serial (1, . . . ,1) which consists of only ’1’ as entries. However, one can easily check that in this case Siis not MDS for anyi≥1. We state this observation as a fact:
Fact 2. Let S = Serial (1, . . . ,1) be an n×n be defined overF2m. Then Si is not MDS for anyi≥1.
Following Fact 2, the lightest possible recursive matrix could be of the form S = Serial (a0, . . . , an−1) where ai = 1 for some 06 ≤ i≤n−1 and aj = 1 for every 0≤j6=i≤n−1. Our objective is to find the lightest possible such matrix for which Si is MDS with the minimumi≥n.
In practice size of the diffusion matrix used in a lightweight block cipher is 4×4. Keeping this in mind we fixn= 4 in the remaining part of this Section. In [10] authors show that if S = Serial (a0, a1, a2, a3) is such thatai= 1 for more than 2 values ofithen S4is never MDS over
F2m.If we relax the condition that S4 need to be MDS and consider matrices such that Si is MDS fori >4, then we get new serial matrices which are the lightest possible. In the following we analyze MDS property of Si, where S = Serial (a0, a1, a2, a3) such that a
i = 1 for 3 values ofi
Theorem 1. Let S = Serial (a0, a1, a2, a3) be a serial matrix defined over F2m
in whichai= 1for precisely 3values ofi. For1≤i≤8the matricesSi are not MDS if
(i) S = Serial (a,1,1,1) (ii) S = Serial (1, a,1,1) (iii) S = Serial (1,1,1, a),
wherea /∈ {0,1}.
Proof. Let S = Serial (a0, a1, a2, a3) be a serial matrix defined overF2m. From (7) it follows directly that fori = 1,2,3 the matrix Si has 0 entries and hence cannot be MDS. Remains to show that Si is not MDS for 4≤i≤8 whenever S is in any of the form (i),(ii),(iii) as given in theorem. We do this by considering each form separately. In the following we denote the polynomial associated with the serial matrix S byf(X)
Case 1.S = Serial (a,1,1,1), a /∈ {0,1}.
The polynomial corresponding to the serial matrix S isf(X) =a+X+X2+ X3+X4 from which it follows that
X7modf(X) = 0 + 0·X+a X2+ (a+ 1)X3.
Note that this polynomial has zero coefficients and that these coefficients form a row in the matrices Si for 4
of these matrices can be MDS. Using same argument we see that the matrix S8 cannot be MDS because the coefficients of
X10modf(X) =a2+ 0·T+ (a2+ 1)·T2+ 0·T3. form a row in this matrix.
Case 2.S = Serial (1, a,1,1), a /∈ {0,1}. In this case we see that
X7modf(X) = (a+ 1) + (a2+a)·X+a·X2+ 0·X3, and (11a) X8modf(X) = 0 + (a+ 1)
·X+ (a2+a)
·X2+a
·X3. (11b)
Using the argument as in Case 1 we see that the matrices Si cannot be MDS for 4≤i≤7 because of zero coefficients in (11a) and the matrixS8 cannot be MDS because of zero coefficients in (11b).
Case 3.S = Serial (1,1,1, a), a /∈ {0,1}.
Unlike previous cases, here all the matrices Si contain non zero entries for 4≤ i≤8. However each of this matrix has a 2×2 singular submatrix. To prove this first note that
X7modf(X) =a3+ 1 + (a3+a2)X+ (a3+a2+a)X2+ (a4+a2)X3 (12a) X8modf(X) =a4+a2+ (a4+a3+a2+ 1)X+
(a4+a3)X2+ (a5+a2+a)X3 (12b)
For i ≥ 1 let Ri = (ri,0, ri,1, ri,2, ri,3) where ri,j is the Coefficient of Xj in the polynomial (Ximodf(X)). Using (7) we know that R7, R8 occur as two consecutive rows in the matrices Si for i = 5,6,7. From (12a) and (12b) it is easy to see thatr7,0r8,2+r8,0r7,2= 0 which implies that the matrices Si have a 2×2 singular submatrix fori= 5,6,7 and hence are not MDS matrices. Finally it remains to show that S8 is also not MDS. We have
X10modf(X) = (a6+a4+a2) + (a6+a5+a4+a)X+
(a6+a5+a2+a)X2+ (a7+a4+a+ 1)X3 (13) and
X11modf(X) =a7+a4+a+ 1 + (a7+a6+a2+a+ 1)X+
(a7+a6+a5+ 1)X2+ (a8+a6)X3 (14) The rows R10, R11 occur in the matrix S8 and from (13) and (14) we see that the sub matrix
r10,1, r10,2 r11,1, r11,2
(15)
is a singular submatrix of S8making it non MDS.
u t
Theorem 2. Let S = Serial (1,1, a,1)be defined over F2m, thenSi is notMDS
(1) If the minimal polynomial ofaoverF2 isX4+X+ 1
(2) If the degree of the minimal polynomial ofaoverF2is≥5and the minimal
polynomial is not in the set{X5+X4+X2+X+ 1, X5+X3+X2+X+ 1, X5+X4+X3+X2+ 1
}
Proof. Let f(x) = 1 +x+a x2+x3+x4 be the associated polynomial of the serial matrix S = Serial (1,1, a,1) from which we can easily see that
x7modf(x) = 0 + (a+ 1)x+a x2+ (a2+a)x3.
Using the argument as in Case 1 of Theorem 1 we conclude that Si is not MDS for 1≤i≤7.
To prove the remaining part of the theorem denote by S(x) the matrix of the form Serial (1,1, x,1) where x is an indeterminate. Let ∆i be the set of determinants of all of thei×isubmatrices of S8(x). We have
∆1={x3+x2+x, x3+x2+x+ 1, x4+ 1, x2, x2+ 1, x, x4+x2, x2+x, x3+x+ 1
}
∆2={x6+x5+x+ 1, x5+x4+x, x5+x3+x2+ 1, x5+x3+x, x6+x4+ 1, x6+x2, x4+x2, x4+x3, x7+x6+x5+x3+x+ 1, x5+x, x6+x4+x3+x2+x, x6, x4+ 1, x6+x5+x4+x,
x7+x5+x3+x, x5+x4+x3+x, x8+x6+x2+ 1, x7+x6+x3+ 1} ∆3={x3+x2+x, x3+x2+x+ 1, x4+ 1, x2, x2+ 1, x, x4+x2, x2+x, x3+x+ 1
} and ∆4={1}.
Denote by∆the set of irreducible factors of polynomials in∆1∪∆2∪∆3. It is easy to see that,
∆={x, x+ 1, x2+x+ 1, x3+x+ 1, x3+x2+ 1, x4+x3+ 1, x4+x3+x2+x+ 1,
x5+x4+x2+x+ 1, x5+x3+x2+x+ 1, x5+x4+x3+x2+ 1 }
Now, if we consider the matrix S(a) for some a ∈ F2m then S(a)8 is MDS if and only if δ(a) 6= 0 for every δ(x) ∈ ∆. One can check that this happens precisely in either the two cases (1), (2) stated in statement of theorem. ut
Corollary 1. The matrix S = Serial (1,1, α,1) defined over F24, where αis a
root of irreducible polynomial X4+X+ 1 is the lightest serial matrix such that S8 is MDS, andXOR (S) = 13.
Proof. As Serial (1,1,1,1) can never be MDS for any (Serial (1,1,1,1))i, thus the next possibility that (Serial (a0, a1, a2, a3))8 is MDS when it is of the form Serial (1,1, a,1) for somea /∈ {0,1}. The elementαwhich is a root ofX4+X+1 = 0 has the lowest nonzero XOR count which is 1. This results in that S is the lightest serial matrix such that S8 is MDS, and XOR (S) = 13.
4
Lightweight Architecture for Block Ciphers: A case
study on
LED
In this section, we will describe the hardware implementation of datapath of typ-ical AES-like block ciphers. We consider the particular instance ofLED, though the idea can be generalized for a larger class of block ciphers having an MDS block as diffusion layer. Along with implementing the above discussed lightweight linear layer, we focus on two other important aspects: 1) the design of the non-linear S-box, and 2) the overall composition of the layers to ensure that the two-fold increase in the iteration requirement of the modified linear layer does not lead to a double increase in the latency. We start with discussion on the the non-linear S-box.
We have implemented the datapath ofLED, using an ASIC design flow. We have used Synopsys Design Compiler(version: vI-2013.12-SP5-4) for synthesis and Synopsys VCS(version: I-2014.03-SP1-1) for simulation. Standard cell li-brary(TSL18FS120) on 180nm technology from TowerSemiconductor Ltd. is used during synthesis, which is characterized usingSiliconSmart Software (ver-sion: 2008.02-SP1p1)underFast-Fast process(P),1.98V voltage(V)and-40 de-gree C temperature(T).
4.1 Choosing an efficient 4×4 S-box
The 4×4 S-box that is used inLEDhas nonlinearity 4, differential uniformity 4, and algebraic degree 3. The polynomial expression overF24 of this S-box is
(α3+α2+ 1)x14+ (α3+α2+ 1)x13+ (α3+α2)x12+ (α3+α2+α)x11
+(α3+ 1)x10+ (α3+ 1)x9+ (α2+α+ 1)x8+α2x7+ (α3+α2)x6 +(α3+α)x5+ (α3+α2+α)x4+ (α2+α+ 1)x3+ (α2+α+ 1)x2+α3+α2, whereαis a primitive root ofX4+X+1 = 0. Instead an S-box which is monomial would have low hardware footprint. The monomialsX 7→Xifori= 7,11,13,14, are such that the associated 4×4 S-box has nonlinearity 4, differential uniformity 4, and algebraic degree 3. We consider such monomial with the least i, i.e., X 7→ X7. As this S-box has fixed points: 0
7→ 0, 1 7→ 1, etc., we consider X 7→ X7+ 1. The associated S-box will thus not have any fixed points, while the other cryptographic properties like nonliearity, differential uniformity, degree remain invariant. The proposed S-box values are shown in Table 4.1.
x 0 1 2 3 4 5 6 7 8 9 A B C D E F S(x) 1 0 A C 8 F 7 6 D 4 9 2 E 3 5 B
We also evaluate that the implementation cost of this S-box is lesser than that ofLED. We implement the proposed S-box function asX7=X4
×X2
×X, which requires 2 nibble wise multiplication operation, 1 square and 1 fourth power calculation followed by one bit XOR . We did not not choose X7 =X4
×X3, as X3 is heavier than the 2 multiplication operations in case of the former decomposition. Our proposed 4×4 S-box occupies 359um2 area, which is 28.6 GE. Here 1 GE is the area required for one 2-input NAND gate. A 2-input lowest drive NAND gate of our library occupies 12.544 um2 area. This design may be compared with the standard look-up table basedLEDS-box implementation occupies 391um2, which is 31.2 GE, which is 9% more than the proposed S-box. We compare the two designs with respect to both cryptographic strengths and area requirement using the S-Box Evaluation Tool (SET) [15] tool in Table 4.1. It may be observed that we have reduced the hardware overhead of the non-linear layer using our proposed method without compromising on security parameters like non-linearity, differential uniformity and degree of a typical 4×4 S-box as used inLED.
Property Proposed S-boxLEDS-box
Nonlinearity 4 4
Algebraic Degree 3 3
Algebraic Immunity 2 2
Differential Uniformity 4 4
Robustness to Differential Cryptanalysis 0.750 0.750
Silicon Area 359um2 391um2
Table 2.S-box Properties as Evaluated by S-Box Evaluation Tool
4.2 Implementing Lightweight Serial Matrix
In this section we describe the implementation strategy of our new lightweight MDS matrix and compare it with existing MDS matrix used inLED. Denote by S1 the serial matrix Serial (α2,1, α, α) which is the existing diffusion matrix of
LED block cipher. This matrix is considered to be lightest which has XOR (S1) = 16 with S4
1 being MDS. We implemented S1×X, whereX = [x1, x2, x3, x4]tis a column vector, each element xi of the vector is a nibble. This implementation has hardware footprint 387.5um2 (31 GE) comprising of six 3-input XOR gates and two 2-input XOR gates.
Next consider the serial matrix S2 = Serial (1,1, α,1) as given in Corollary 1. This serial matrix is lighter than S1 with XOR cost 13, using which MDS matrix is calculated as S8
We design the entire data-path of LED using proposed transformation and the overall design results show compaction. The critical path length and the overall area of the linear layer and the entire data-path is shown in Table 3 below. From the table it can be seen that there is saving of 16% area in the proposed datapath (1044.6 GE) compared to the originalLEDdatapath (1244.2 GE). However, one may argue that in the proposed linear layer result obtained by computing S8
2×X, (Xis the state matrix) requiring 8 clock cycles, whereas in the originalLEDdesign the linear layer result is obtained from S4
1×X which requires only 4 clock cycles. So it may seem that the new design incurs twice latency compared to the original design for one round implementation. Our proposed S-box takes lesser time to execute, notably, delay for the S-box and shift row combined is 2.47 ns forLED, whereas for the new design it is just 1.63 ns. This helps reduce the overall delay in our design not reaching the double the delay of LED. Then overall latency of theLEDis 0.61×4 + 2.47 = 4.91 ns, while that for the new design it is 0.61×8 + 1.63 = 6.51 ns. Thanks to lower latency incurred by the S-box, the overall increase in latency of the new design is capped at 30%. In IoT applications low area footprints is always a factor, whereas in some applications like environment monitoring some latency is affordable. So, for these class of applications our design has very high impact.
Design Crdatapath(ns)?? Crlinearlayer(ns)Adatapath (GE)Alinearlayer(GE)
LED 3.08 0.61 1244.2 123.56
Our Design 2.24 0.61 1044.6 116.5
Table 3.Area and Critical Path Time Comparison for one round implementation of our design andLED
4.3 Restraining Latency by Double Clock Architecture
The new lightweight MDS matrix S2 requires 8 iterations to compute the full effect of diffusion layer since S8
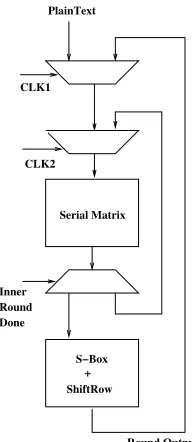
2 is MDS. Compared to original matrix S1 which needs 4 iterations the matrix S2 increases latency. We now describe a solution for reducing the latency caused by our serial matrix implementation. If the user wants to have very low area footprint like our design, and also wants to have low latency, then following is our suggestion. One can use double clock architecture to check the latency of the new design. We present this in Figure 1. The figure shows the operation of the serial matrix is done at a clock clk2 which is faster than clk1, rests of the operations are done at clk1. With this architecture we can curb the latency and at the same time can benefit from the low area cost.
?? This latency is due to one iteration of serial matrix along with S-box implementation
CLK1
CLK2
Inner Round Done
ShiftRow + S−Box PlainText
Round Output Serial Matrix
Fig. 1.Datapath Design of our Proposed Method
Design Crdatapath(ns)Crlinearlayer(ns) Adatapath(GE)Alinearlayer(GE)
LEDblock Cipher 3.08 0.61 1709.4 123.56
P roposed M ethod 2.24 0.61 1640 116.5
Table 3.Area and Critical Path Time Comparison
5
Conclusions
Latency is inherent to the block ciphers whose di↵usion layer is based on serial matrix. In this work we have shown that if we relax latency slightly we can further reduce the implementation cost of the di↵usion layer. We apply our newly discovered matrix in the di↵usion layer ofLED, and on top of that we also propose a lighter S-box for LED. The combining e↵ect of these two is that we get a variant ofLEDwhich is lighter than the original one. We further employ in these ideas in a multi-clock design of the LED data-path which can be used to keep the latency increase at a check of 1.3, while the overall gate count (area) is reduced by around 1.04 per round ofLED. With this we open up the applicability of n⇥n serial matrix S in lightweight block ciphers, such that Si is MDS for i > n.
References
1. D. Augot and M. Finiasz. Exhaustive search for small dimension recursive mds di↵usion layers for block ciphers and hash functions. InInformation Theory
Pro-Fig. 1.Datapath Design of our Proposed Method
5
Conclusions
Latency is inherent to the block ciphers whose diffusion layer is based on serial matrices. In this work we have shown that if we relax latency slightly, then we can further reduce the implementation cost of the diffusion layer. We have applied our newly discovered matrix in the diffusion layer ofLED, and on top of that we also have proposed a lighter S-box. The combining effect of these two is that we have obtained a variant ofLEDwhich is lighter than the original one. We also have proposed a multi-clock design of the LEDdata-path which can be used to restrain increase in the latency.
Our diffusion matrix opens up the applicability of ann×n serial matrix S in lightweight block ciphers, such that Si is MDS fori > n. On the other hand, the proposed multi-clock architecture is also interesting to explore further.
References
1. D. Augot and M. Finiasz. Exhaustive Search for Small Dimension Recursive MDS Diffusion Layers for Block Ciphers and Hash Functions. In Information Theory Proceedings (ISIT), 2013 IEEE International Symposium on, pages 1551–1555. IEEE, 2013.
2. D. Augot and M. Finiasz. Direct Construction of Recursive MDS Diffusion Lay-ers using Shortened BCH Codes. In International Workshop on Fast Software Encryption, pages 3–17. Springer, 2014.
3. A. Bogdanov, L. R. Knudsen, G. Leander, C. Paar, A. Poschmann, M. J. B. Rob-shaw, Y. Seurin, and C. Vikkelsoe. PRESENT: An Ultra-Lightweight Block Cipher. In P. Paillier and I. Verbauwhede, editors,Cryptographic Hardware and Embedded Systems - CHES 2007, volume 4727 ofLNCS, pages 450–466. Springer, 2007. 4. J. Borghoff, A. Canteaut, T. G¨uneysu, E. B. Kavun, M. Kneˇzevic, L. R. Knudsen,
G. Leander, V. Nikov, C. Paar, C. Rechberger, P. Rombouts, S. ren S. Thomsen, and T. Y. in. PRINCE - A Low-latency Block Cipher for Pervasive Computing Applications (Full version). Cryptology ePrint Archive, Report 2012/529, 2012.
http://eprint.iacr.org/.
5. J. Daemen and V. Rijmen. The Design of Rijndael: AES - The Advanced Encryp-tion Standard. InformaEncryp-tion Security and Cryptography. Springer, 2002.
6. J. Guo, T. Peyrin, and A. Poschmann. The PHOTON Family of Lightweight Hash Functions. In P. Rogaway, editor,Advances in Cryptology - CRYPTO 2011 - 31st Annual Cryptology Conference, Santa Barbara, CA, USA, August 14-18, 2011. Proceedings, volume 6841 of Lecture Notes in Computer Science, pages 222–239. Springer, 2011.
7. J. Guo, T. Peyrin, A. Poschmann, and M. J. B. Robshaw. The LED Block Ci-pher. In B. Preneel and T. Takagi, editors,Cryptographic Hardware and Embedded Systems - CHES 2011, volume 6917 ofLNCS, pages 326–341. Springer, 2011. 8. K. C. Gupta, S. K. Pandey, and A. Venkateswarlu. On the Direct Construction of
Recursive MDS Matrices. Designs, Codes and Cryptography, 82(1-2):77–94, 2017. 9. K. C. Gupta, S. K. Pandey, and A. Venkateswarlu. Towards a General Construction of Recursive MDS Diffusion Layers.Designs, Codes and Cryptography, 82(1-2):179– 195, 2017.
10. K. C. Gupta and I. G. Ray. On Constructions of MDS Matrices from Companion Matrices for Lightweight Cryptography. InInternational Conference on Availabil-ity, ReliabilAvailabil-ity, and SecurAvailabil-ity, pages 29–43. Springer, 2013.
11. K. Khoo, T. Peyrin, A. Y. Poschmann, and H. Yap. FOAM: Searching for Hardware-Optimal SPN Structures and Components with a Fair Comparison. In L. Batina and M. Robshaw, editors, Cryptographic Hardware and Embedded Sys-tems - CHES 2014, volume 8731 of Lecture Notes in Computer Science, pages 433–450. Springer Berlin Heidelberg, 2014.
12. M. Liu and S. M. Sim. Lightweight MDS Generalized Circulant Matrices. In T. Peyrin, editor,Fast Software Encryption - 23rd International Conference, FSE 2016, Bochum, Germany, March 20-23, 2016, Revised Selected Papers, volume 9783 ofLecture Notes in Computer Science, pages 101–120. Springer, 2016. 13. F. J. Macwilliams and N. J. A. Sloane. The Theory of Error-Correcting Codes
(North-Holland Mathematical Library). North Holland, January 1983.
15. S. Picek, L. Batina, D. Jakobovi´c, B. Ege, and M. Golub. S-box, SET, Match: A Toolbox for S-box Analysis. In D. Naccache and D. Sauveron, editors, 8th IFIP International Workshop on Information Security Theory and Practice (WISTP), volume LNCS-8501 ofInformation Security Theory and Practice. Securing the In-ternet of Things, pages 140–149, Heraklion, Crete, Greece, June 2014. Springer. Part 5: Short Papers.
16. M. Sajadieh, M. Dakhilalian, H. Mala, and P. Sepehrdad. Recursive Diffusion Layers for Block Ciphers and Hash Functions. InFast Software Encryption, pages 385–401. Springer, 2012.
17. S. Sarkar and S. M. Sim. A Deeper Understanding of the XOR Count Distribu-tion in the Context of Lightweight Cryptography. In D. Pointcheval, A. Nitaj, and T. Rachidi, editors,Progress in Cryptology - AFRICACRYPT 2016 - 8th In-ternational Conference on Cryptology in Africa, Fes, Morocco, April 13-15, 2016, Proceedings, volume 9646 of Lecture Notes in Computer Science, pages 167–182. Springer, 2016.
18. S. Sarkar and H. Syed. Lightweight Diffusion Layer: Importance of Toeplitz Ma-trices. IACR Trans. Symmetric Cryptol., 2016(1):95–113, 2016.
19. S. Sarkar and H. Syed. Analysis of Toeplitz MDS Matrices. Cryptology ePrint Archive, Report 2017/368, 2017. http://eprint.iacr.org/2017/368.
20. T. Shirai, K. Shibutani, T. Akishita, S. Moriai, and T. Iwata. The 128-Bit Blockci-pher CLEFIA (Extended Abstract). In A. Biryukov, editor,Fast Software Encryp-tion, 14th International Workshop, FSE 2007, Luxembourg, Luxembourg, March 26-28, 2007, Revised Selected Papers, volume 4593 ofLecture Notes in Computer Science, pages 181–195. Springer, 2007.
21. S. M. Sim, K. Khoo, F. Oggier, and T. Peyrin. Lightweight MDS Involution Matrices. In G. Leander, editor,Fast Software Encryption, volume 9054 ofLecture Notes in Computer Science, pages 471–493. Springer Berlin Heidelberg, 2015. 22. S. Vaudenay. On the Need for Multipermutations: Cryptanalysis of MD4 and
SAFER. InFast Software Encryption, pages 286–297. Springer, 1995.