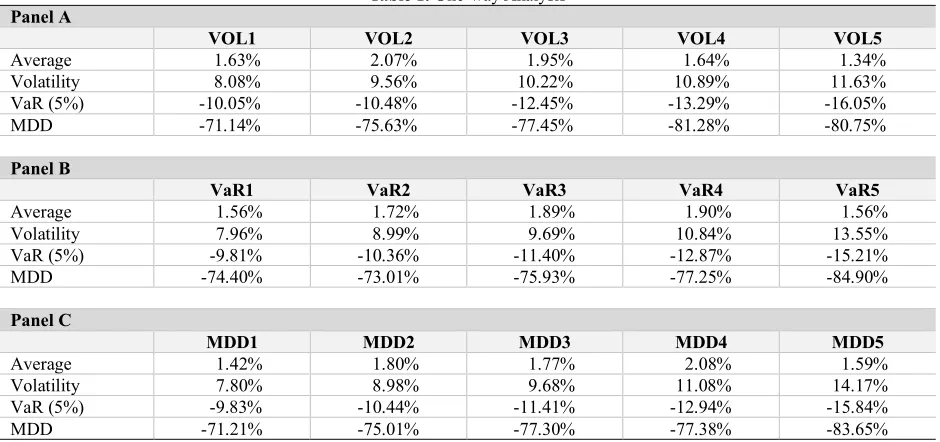
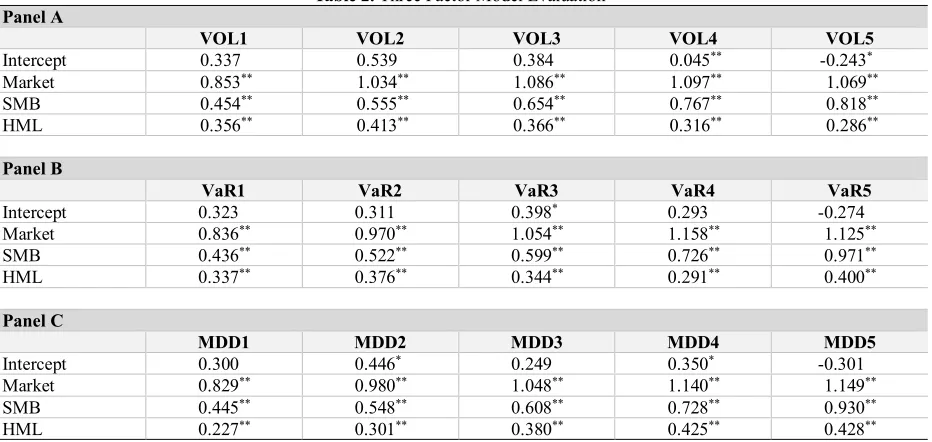
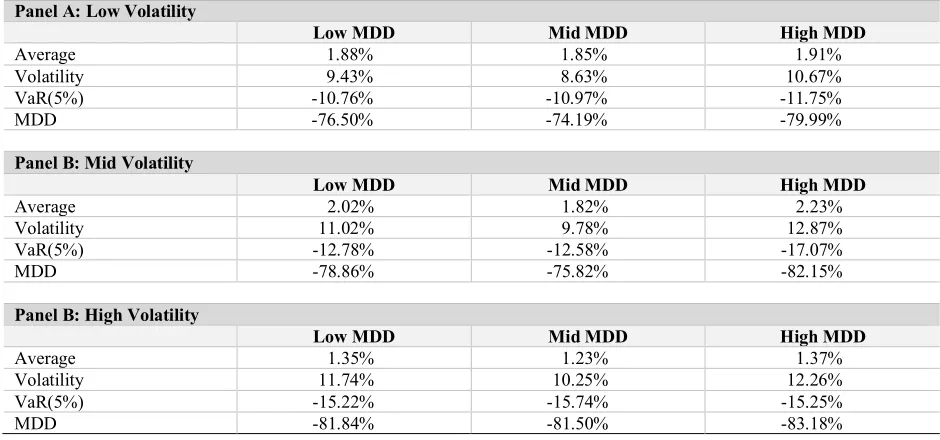
Are Value At Risk And Maximum Drawdown Different From Volatility In Stock Market?
Full text
Figure
Related documents
In particular, restorative justice holds the key not only to protecting different rights, but also to the restoration of the dignity of the victim, the transgressor and
collaboration, and science content knowledge at Cori Elementary School. The review of the literature will focus on four research questions: 1) What kinds of
A recent study by IFPRI shows that if investments in public agricultural research doubled from US$5 to US$10 billion from 2008 to 2013, agricultural output would increase
Using reports from the Petroleum Transparency and Accountability (P-TRAC) Index, published by the Institute of Economic Affairs (IEA- Ghana), as the basis for research
En el segundo capítulo ―Efecto del tratamiento térmico sobre el perfil de ácidos grasos en leches‖, se evalúa el efecto de la homogenización (65ºC, 250 bar) y la
AxleDB Accelerators Unit (AAU). In this section, we explain the overall organiza- tion and interconnection of AxleDB accelerators. AxleDB is equipped with a set of hardware
A fourth educational approach to software engineering education emerged by explicitly identifying the processes needed to do design and teaching those skills directly [21- 23].
The successful Vendor shall provide and pay for performance and payment bonds for projects in excess of $100,000. Such bonds shall cover the full and faithful performance of