International Journal of Emerging Technology and Advanced Engineering
Website: www.ijetae.com (ISSN 2250-2459, ISO 9001:2008 Certified Journal, Volume 9, Issue 10, October 2019)
292
Second-Order Efficiency for Estimating the Product of k Means
Xing Xia
1, Kamel Rekab
2Department of Mathematics and Statistics, University of Missouri-Kansas City. Kansas City, MO, USA
Abstract-- In order to estimate the reliability of sequentially designed procedures in broader applications, we derived the second-order lower bound of the Bayes risk for the product of k means of independent populations under the Bayesian framework. The trials of samplings are from the one-parameter exponential family, which generalize the result to wider practical applications. In this article, we propose and test the derived result in three-stage sampling design by using Monte Carlo simulations. The proposed three-stage sampling design is shown to be second order efficient.
Keywords:Bayes risk; Second-order lower bound; Product of k means; Three-stage sampling design; One-parameter exponential family; Reliability estimation; Monte Carlo simulation.
I. INTRODUCTION
The most common application of estimating the product of k means is to test software accuracy, also known as reliability testing, which many fields and industries have heavily relied on. Testing samples for reliability follows Bernoulli distribution in this particular application.
However, other applications, like risk assessment, we can find different distributions such as Normal, Poisson, etc. which are all in the one-parameter exponential family. We wanted to generalize the result to wider applications.
(Benkamra Z. T., 2015) derived nearly second order efficiency under classic linear function framework with samples from Bernoulli distribution. For nonlinear functions which are known as Bayesian framework, (Rekab & Song, 2017) derived first order efficiency for k independent components with samples from the one-parameter exponential family. (Xia & Rekab, 2019) derived second order efficiency for 2 independent components, and later on derived the second order efficiency for k independent components.
In this study, we generalize the result to the one-parameter exponential family under Bayesian framework based on the previous study (Xia & Rekab, 2019), and present the three-stage sampling schemes with Monte Carlo simulations.
II. MATERIALS AND ASSUMPTIONS
Let * + be a sequence of independent random variables with distributions belonging to the
one-parameter exponential family, that is
( ) { ( )} ( ) ( )
where and ( ).
Let field * + be a collection of subsets of , where is -algebra generated by * +. It is equivalent to say that contains complete information about the procedure among populations. Therefore, for each , we have
which is a key in using the martingale concept in this study.
By adopting the Bayesian approach, the conjugate prior ( ) for ( ) and the posterior density ( )are from the
same family.
The density function of conjugate prior is
( ) { ( )} ( )
( )
where
International Journal of Emerging Technology and Advanced Engineering
Website: www.ijetae.com (ISSN 2250-2459, ISO 9001:2008 Certified Journal, Volume 9, Issue 10, October 2019)
293
Then mean and variance of the prior distributions are, ( )- ∫ ( ) ( ) ( )
( ( )) 0( ( ) ) 1
, ( ( )
The posterior density function is
( ) { ( )} ( )
( )
where
( ) ∫ { ( )} ( )
with
∑
( )
Then mean and variance of the posterior distributions are
, ( ) - ( ( ) ) * ( )
| + ( )
To estimate the reliability of a series system is to use the product of the reliability of each independent component, which is the mean of samples, that is,
∏
∏ ( )
( )
With the choice of square error loss function ( ̂) ( ̂) , and the Bayes estimate for each individual , ̂
, ( ) -, the assumption of independence among means that the Bayes estimate of their product is the product of their posterior means, that is
̂( ) [∏ ( )
| ] ( )
and the estimate that minimizes the Bayes risk is the expected posterior loss, namely
( ) ,( ̂) - ,( , -) - * (∏ ( )
) | + ( )
III. RESULTS
For ( ) independent components in the series system, let the total number of samples ∑ and is fixed.
The Bayes risk can be written as
( ) [∑ [ ( ( ) ) ∏ [ ( )| ]] ∑ ∑ (∏ ( ( ) )∏ [ ( )| ])]
[∑ [ ( ( )
| ) ∏ [ ( )| ]]
∑ ∑ (∏ ,(
( )
∏ [ ( )| ])
]
[∑ 0 1 ∑ ∏
International Journal of Emerging Technology and Advanced Engineering
Website: www.ijetae.com (ISSN 2250-2459, ISO 9001:2008 Certified Journal, Volume 9, Issue 10, October 2019)
294
where , ( ) - ∏ [ ( )| ] , and
∏ , ( ) - ∏ [ ( )| ] .
where * +, and is a class of subsets of with exact elements. For example, let then *( ) ( ) ( ) ( ) ( ) ( )+.
Theorem 3.1
For any sequential procedure , Suppose that ( ) for all and ( ) is second-order and third-order continuously differentiable almost everywhere in its domain.
i. ∫ ( ) ∫ ( )
ii. Let ∑ which is the total sample size and is fixed
iii. √
( ) ∏ ( )
∑ (√ ( ) ∏ ( )
)
∑
Thus, we have the second order lower bound of the k components Bayes risk as
( ) [.∑ / ]
(
[
∑
∏ ( )]
)
. / ( )
where √ ( ) ∏ ( )
.
Remark: in this study, we use standard notations for asymptotic comparison:
( ) ( ( )) if and only if there exists a positive real number and a real number such that ( ) ( ) for all .
Proof: From (3.1)
( ) [∑ ∑ ∏
]
*.∑ √ / ∑ ∑ ∑ ( √ √ ) ∏
∑ ∏
+ ( )
*.∑ √ / ∑ ∏
+ ( )
Since the second term of equation (3.3) is non-negative, (3.4) is established with equality when ∑√ √ To further derive the second term of (3.4),
[∑ ∏
] ,∑ ∏
-
*∑
International Journal of Emerging Technology and Advanced Engineering
Website: www.ijetae.com (ISSN 2250-2459, ISO 9001:2008 Certified Journal, Volume 9, Issue 10, October 2019)
295
*∑+ ( )
*∑ .∑ √ / √
+ ( )
,.∑ √ / ∑ √
. /
Therefore,
( ) [.∑ √ /
.∑ √ / ∑ √
. /]
[.∑ √ / ](
,(∑ √
)-) . / ( )
Lemma 3.2 If in probability for each ∑ ,then
√ √ , ( ) - ∏ [ ( )| ]
√ ( ) ∏ ( )
,
∏ , ( ) - ∏ [ ( )| ] ∏ ( ) ∏ ( )
Proof: Since the conditional expectations [ ( )| ] and [ ( )| ] are martingales for each with random stopping time , the proof follows by the optimal sampling theorem and the martingale convergence theorem.
IV. THREE STAGE SAMPLING DESIGN Let , be the cumulative total number of cases sampled after each stage. The key ratio, is involved in each stage as well.
√ ( ) ∏ ( ) ∑ √ ( ) ∏ ( )
( )
Stage 1:
Assume that , and let ⌊√ ⌋ which is the sample size from each population. Now we refine the key ratio in (4.1) by using its posterior expectation with the first stage’s sample size, that is
̂ [ | ] ( )
where ∑ and is subject to
International Journal of Emerging Technology and Advanced Engineering
Website: www.ijetae.com (ISSN 2250-2459, ISO 9001:2008 Certified Journal, Volume 9, Issue 10, October 2019)
296
Stage 2:Let ⌊ ⌋ which is the cumulative total sample size after second stage and ; it suffices that can be an
arbitrary constant between √ and 1, namely, √ .
After setting the total sample size for the second stage, we update sample sizes from each component based on the estimated key ratio obtained from stage 1 as
{ ( ) {⌊( ) ̂ ( )⌋ }}
* ( ) * ∑
++
where is subject to ( ) . It is possible that the total amount of sampling cases is less than , we will just need to update by totaling sample size from each component. The estimate of the key ratio in (4.3.1) can be future refined as
̂ [ ̂ | ] ( )
Since is arbitrary, is allowed to vary under conditions ( ) .
Stage 3:
In this stage, the remaining samples, , will be allocated to each component based on and updated ̂ from stage 2, such that
{ ∑
{⌊( ) ̂ ( )⌋ }}
{ ∑
{ ∑ }}
This procedure also shows that the sample sizes from the second stage, , is in-between and ( ) , the in the third stage is in-between and ∑ .
V. MONTE CARLO SIMULATION
We use 3 independent components from Bernoulli distribution to reduce the computational expense through Monte Carlo simulation.
Suppose that ( ) are three independent components, Bernoulli distributed random variables with means , where are unknown, represent reliability of the independent components respectively which follow Beta distribution.
( ), where ; Let
From (3.2), we get the second order lower bound for three components case in Bernoulli distribution, that is
( ) [.√ ( ) √ ( ) √ ( ) / ]
( [√( )√( )
√
√( )√( ) √
√( )√( )
√ ]) . / ( )
International Journal of Emerging Technology and Advanced Engineering
Website: www.ijetae.com (ISSN 2250-2459, ISO 9001:2008 Certified Journal, Volume 9, Issue 10, October 2019)
297
( )0 , ( ) - , - , - , ( ) - , - , - , ( ) - , - , - , ( ) - , ( ) - ,
, ( ) - , ( ) - , - , ( ) - , ( ) - , - , ( ) - , ( ) - , ( )
-1
*
( )( )( ) (
) +
*
( )( )(
) (
) +
*
( )( )(
) (
) +
* ( ) ( )
( )( )( ) +
* ( ) ( )
( )( )( ) +
* ( )( )
( ) ( )( ) +
[ ( )( )
( ) ( )
( ) ( )] ( ) Now we use Monte Carlo simulation to simulate the three-stage design.
Let
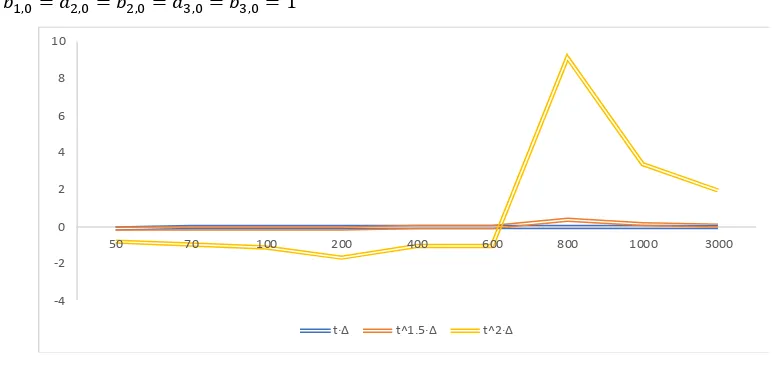
Figure 5.1 ( ) ( ) is bounded by as , where
Now let’s try
-4 -2 0 2 4 6 8 10
50 70 100 200 400 600 800 1000 3000
[image:6.612.104.491.442.625.2]International Journal of Emerging Technology and Advanced Engineering
Website: www.ijetae.com (ISSN 2250-2459, ISO 9001:2008 Certified Journal, Volume 9, Issue 10, October 2019)
298
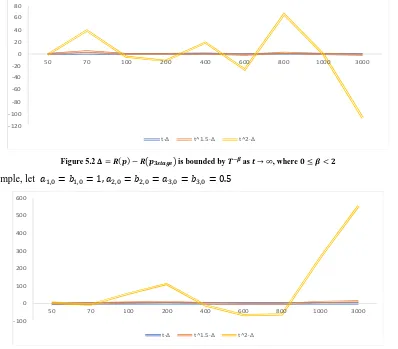
Figure 5.2 ( ) ( ) is bounded by as , where
Another example, let
Figure 5.3 ( ) ( ) is bounded by as , where
VI. CONCLUSION
The results of the sampling designs assure us that the second-order lower bound for the product of k-means is a good estimate of Bayes Risk. Due to its generalization, the second order lower bound can be adopted to any distributions within the one-parameter exponential family, both for the distribution of samples and the prior distribution. The efficiency of Bayesian estimation methodology holds for departures from the assumed distributions, as well as the assumed parameters. The robustness of this analysis is worth being developed and proven for future applications.
VII. DATA AVAILABILITY
The data used to support the findings of this study have been produced by Monte Carlo simulations from Bernoulli trials with 5000 replications.
BIBLIOGRAPHY
[1] Ash, R. B. (1972). Real Analysis and Probability. (Z. W. Birnbaum, Ed.) Academic Press.
[2] Benkamra, Z. T. (2013). Bayesian sequential estimation of the reliability of a parallel-series system. Applied Mathematics and Computation 209(23), 10842-10852.
[3] Benkamra, Z. T. (2015). Nearly second order three-stage design for estimating a product of several Bernoulli proportions. Journal of Statistical Planning and Inference.
[4] Billingsley, P. (2012). Probability and Measure. John Wiley & Sons. [5] Billinton, R., & Allan, R. N. (1992). Reliability Evaluation of Engineering Systems, Concepts and Techniques. New York: Springer.
[6] Diaconis, P., & Ylvisaker, D. (1979, March). Conjugate priors for exponential families. The Annals of Statistics, 7 (2), 269-281. [7] HardWick, J. a. (2002). Optimal Few-Stage Designs. Journal of
Statistical Planning and Inference 104, 121-145.
[8] Littlewood, B., & Wright, D. (1997). Some conservative stopping rules for the operational testing of safety critical software. IEEE Transactions on Software Engineering 23 (11), 673-683.
-120 -100 -80 -60 -40 -20 0 20 40 60 80
50 70 100 200 400 600 800 1000 3000
t·Δ t^1.5·Δ t^2·Δ
-100 0 100 200 300 400 500 600
50 70 100 200 400 600 800 1000 3000
[image:7.612.108.506.137.486.2]International Journal of Emerging Technology and Advanced Engineering
Website: www.ijetae.com (ISSN 2250-2459, ISO 9001:2008 Certified Journal, Volume 9, Issue 10, October 2019)
299
[9] Poore, J. H., Mills, H. D., & Mutchler, D. (1993). Planning andcertifying software system reliability. IEEE Software 10 (1), 88-99. [10] Rekab, K. (1990). Asymptotic Optimality of Experimental Designs
in Estimating a Product of Means. Journal of Applied Mathematics and Stochastic Analysis 3(1), 15-25.
[11] Rekab, K. (1992). A nearly optimal 2-stage procedure. Communications in Statistics - Theory and Methods, 21 (1), 197-201. [12] Rekab, K. a. (2000). A two-stage sequential allocation scheme for
estimating the product of several means. Stochastic Analysis and Applications: 18(2), 289-298.
[13] Rekab, K., & Li, Y. (1994). Bayesian Estimation of the Product of Two Proportions. Stochastic Analysis and Applications 12(3), 369-377.
[14] Rekab, K., & Song, X. (2017). First-Order Asymptotic Efficiency in Sequential Designs for Estimating Product of k means in the Exponential Family Case. Jonrnal of Applied Mathematics and Statistics, 4 (1), 50-69.
[15] Song, X. (2016). Generalization of Efficient Sequential Designs for Estimating Product of Means in the One-Parameter Exponential Family Case. PhD Dissertation, University of Missouri - Kansas City, Department of Mathematics.
[16] Woodroofe, M. (1981). A.P.O. Rules are Asymptotically non-Deficient for Estimation with Squared Error Loss. Wahrscheinlichkeitstheorieverw. Gebiete 58, 331-341.
[17] Xia, X., & Rekab, K. (2019, July). Second-Order Efficiency of Bayes Risk for Estimating Reliability of k Components Series Systems. International Journal of Emerging Technology and Advanced Engineering, 9(7), 22-27.