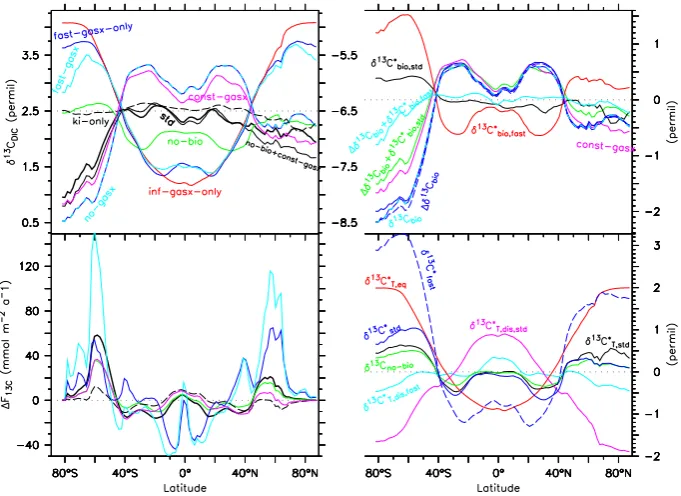
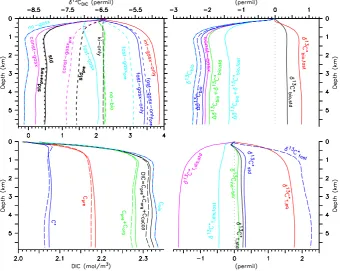
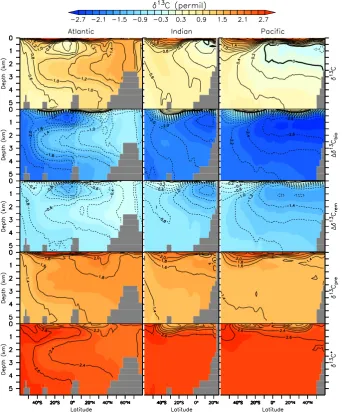
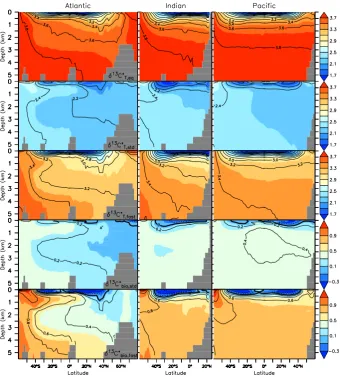
Biology and air–sea gas exchange controls on the distribution of carbon isotope ratios ( 13 C) in the ocean
Full text
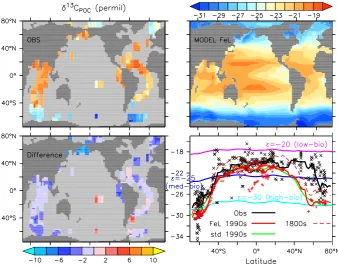
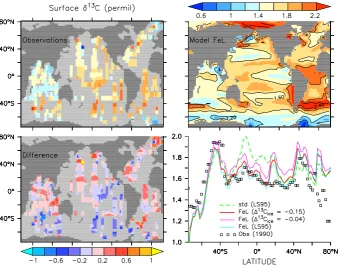
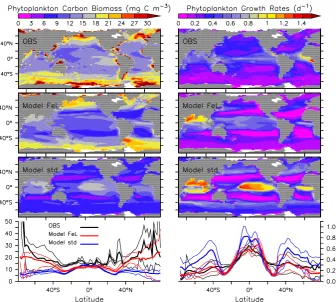
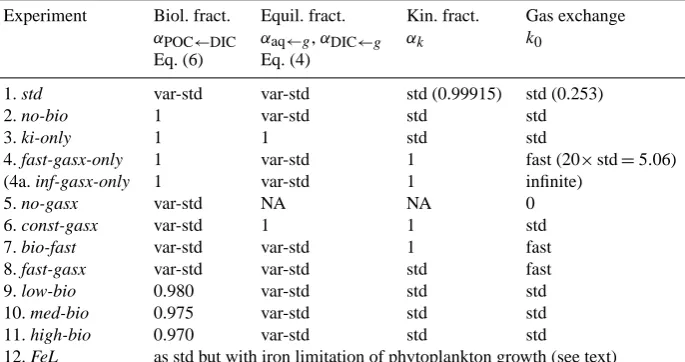
Figure
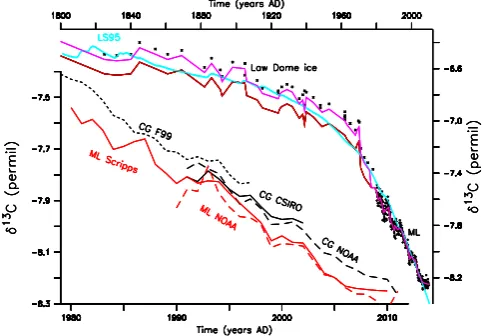
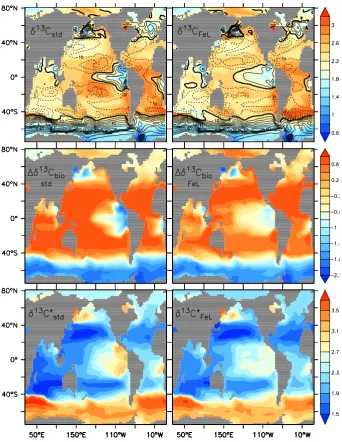
Related documents
The joint modelling of longitudinal and survival data is a valid approach to account for measurement error in the analysis of a repeatedly measured biomarker and a time to event..
Acom: anterior communicating artery; BA: basilar artery; DWI: diffusion- weighted imaging; EDT: embolization of distal territories; ENT: embolization in new territories; HIA:
Figure 1. Body weight changes in normal and ovx rats with and without MECL treatment. Body weight was measured from the start to the end of experiment; # p<0,05 compared with
In this paper the first step toward the implementation and testing of a Direct Computer Mapping based methodology for modeling and dynamic simulation of Recirculating
Absent peritoneal fluid on screening trauma ultrasonography in children: a prospective comparison with computed tomography. The Role of computed tomography in blunt
Using genome-wide overlapping PCR (AmpliSeq), we ob- tained the complete KSHV genome sequence from di ff erent time points of the disease.. These represent one of the few KSHV