ON THE VERTEX-FACE GRAPHS OF TRIANGULATIONS

(1)

ON THE VERTEX-FACE GRAPHS OF TRIANGULATIONS∗

WEIGEN YAN† AND SHULI LI‡

Abstract. LetG= (V(G), E(G)) be a triangulation with vertex setV(G) ={v1, v2, . . . , vn}and edge setE(G) embedded on an orientable surface with genusg. DefineG∇ to be the graph obtained fromGby inserting a new vertexvφto each face

φofGand adding three new edges (u, vφ),(v, vφ) and (w, vφ), whereu, vandware the three vertices on the boundary ofφ. LetG_{be the graph obtained from}_G∇_{by deleting all edges in}_E₍_G_{) of}_G∇_{. In this paper, first some spectral properties of}

G∇andG _{are considered, then it is proved that}_t₍_G∇_{) = 3}n+4g−3₅n−1_t₍_G_{) and}_t₍_G_{) = 3}n+4g−3₂n−1_t₍_G_{), where}_t₍_G_{) is}

the number of spanning trees ofG. As applications, the number of spanning trees and Kirchhoff indices of some lattices in the context of statistical physics are obtained.

Key words. Vertex-face graph, Triangulation, Spanning tree, Kirchhoff index, Degree Kirchhoff index.

AMS subject classifications. 05C30, 05C50, 05C76, 05C90.

1. Introduction. Unless otherwise specified, graphs in this paper are simple. LetAG andDG denote the adjacency matrix and the diagonal matrix of vertex degrees of the graphGwithnvertices, respectively. The matricesLG=DG−AGandLG=D

−1/2 G LGD

−1/2

G are called theLaplacian matrix and thenormalized

Laplacian matrix ofG, respectively. The polynomialsµ(G, x) = det(xIn−LG) andχ(G, x) = det(xIn− LG)

are called the Laplacian characteristic polynomial and thenormalized Laplacian characteristic polynomial

ofG, respectively.

Let G be a triangulation embedded on an orientable surface Σ with genusg with vertex set V(G) = {v1, v2, . . . , vn}, edge setE(G) ={e1, e2, . . . , em}, and face setF(G) ={φ1, φ2, . . . , φf}. The dual graphG⊥

ofGis the graph whose vertices, edges and faces correspond to faces, edges and vertices ofG, respectively. We can embedGandG⊥ simultaneously in Σ such that an edgeeofGcrosses the corresponding dual edge

e⊥ofG⊥ exactly once and crosses no other edge ofG⊥. Hence,V(G⊥) =F(G),E(G⊥) =

e⊥₁, e⊥₂, . . . , e⊥_m , andF(G⊥) =V(G).

By the Eulerian formula,n−m+f = 2−2g. LetV(φ) denote the set of vertices on the boundary of face

φofG. Note that each faceφofG(including the unbounded face) is a triangle. So|V(φ)|= 3 and 2m= 3f. Hence,f = 2n+ 4g−4 andm= 3n+ 6g−6. Now we define two new graphsG∇andG fromG, which are called thevertex-face graphof the first kind and the second kind ofG, respectively, as follows. The vertex sets

V(G∇) andV(G_{) of}_G∇_and_G _{are the union of}_V₍_G_{) and}_F₍_G_{), i.e.,}_V₍_G∇_{) =}_V₍_G_{) =}_V₍_G₎_∪_F₍_G_),

and the edge setsE(G∇) =E(G)∪ {(u, φ)|u∈V(φ), φ∈F(G)}andE(G_{) =}_{(_{u, φ}_)|_u_∈_V₍_φ₎_{, φ}_∈_F₍_G_)}.

Obviously, G∇ is a triangulation with n+f vertices embedded on Σ, and G is a bipartite graph with

n+f vertices and mfaces embedded on Σ. Furthermore,|V(φ)|= 4 for every faceφ∈F(G_{). If}_G_{is the}

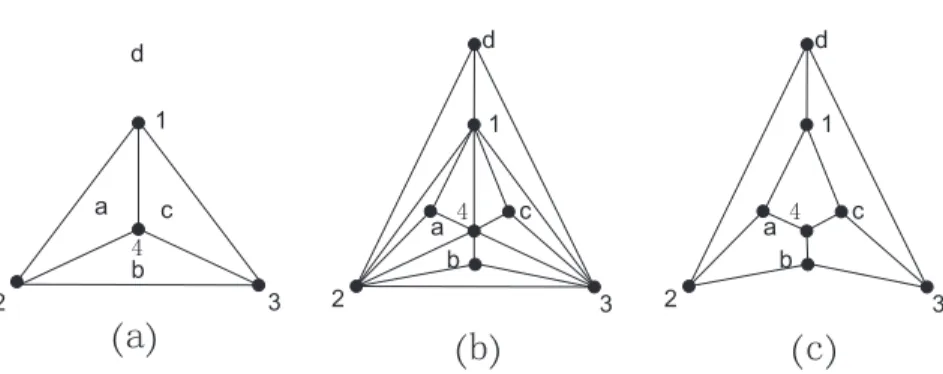
complete graph with four vertices which is embedded on the plane as illustrated in Figure 1(a), then the corresponding vertex-face graphsG∇andG_{are the graphs illustrated in Figure 1(b) and (c), respectively.} ∗_{Received by the editors on July 23, 2018. Accepted for publication on July 20, 2020. Handling Editor: Bryan L. Shader.}

Corresponding Author: Shuli Li.

†_{School of Sciences, Jimei University, Xiamen 361021, China (weigenyan@263.net).}

‡_School _of _Mathematical _and _Computer _Sciences, _Quanzhou _Normal _University, _Quanzhou _362000, _China

(2)

( )

a

_{( )}

_b

_{( )}

_c

1 1 2 2 3 3 4 4 a a b b c c d d 1 2 ₃ 4 a b c d

Figure 1. (a) A plane triangulationGwith vertex set V(G) ={1,2,3,4}and face set F(G) ={a, b, c, d}. (b) The

vertex-face graphG∇ of the first kind ofG. (c) The vertex-face graphG of the second kind ofG.

In this paper, we first consider some spectral properties of G∇ and G _{in Section 2. In Section 3, we}

prove thatt(G∇) = 3n+4g−35n−1t(G) andt(G_{) = 3}n+4g−3₂n−1_t₍_G_{), where}_t₍_G_{) is the number of}_spanning

trees of G, which is also referred to as the complexity of G. In Section 4, we obtain a relation between Kf(G∇), Kf(G_{) and Kf(}_G_{) and also obtain a relation between Kf}0₍_G∇_{), Kf}0

(G_{) and Kf}0₍_G_{), where Kf(}_G₎

and Kf0(G) are theKirchhoff index anddegree-Kirchhoff indexofG, respectively. As applications, in Section 5, we compute the number of spanning trees and Kirchhoff indices of some lattices in the context of statistical physics.

2. Spectral properties ofG∇andG. Suppose thatGis a triangulation embedded on an orientable surface with vertex set V(G) = {v1, v2, . . . , vn}, edge set E(G) = {e1, e2, . . . , em}, and face set F(G) =

{φ1, φ2, . . . , φf}. Define the vertex-face incident matrix as MG = {mij}n×f, where mij = 1 if vertex vi ∈V(φj) and mij = 0 otherwise. For the triangulationG illustrated in Figure 1(a), V(G) = {1,2,3,4} andF(G) ={a, b, c, d}, the vertex-face incident matrixMG is

    1 0 1 1 1 1 0 1 0 1 1 1 1 1 1 0     .

Lemma 2.1. Let G be a triangulation with n vertices and f faces embedded on an orientable surface. Then

MGM_GT =DG+ 2AG,

where MT

G is the transpose of MG, and AG andDG are the adjacency matrix and the diagonal matrix of

vertex degrees ofG, respectively.

Proof. For anyi, j∈ {1,2, . . . , n}, by the definition ofMG,

MGMGT ii= f X k=1 mikmik= f X k=1 mik=di

(3)

and MGMGT ij = f X k=1 mikmjk.

Note thatmikmjk= 1 if and only ifvi, vj ∈V(φk). SinceGis a triangulation, the boundary of each face of Gis a triangle. Sovi, vj ∈V(φk) if and only if (vi, vj) is an edge ofG. Note thatGhas no cut edge (since

Gis a triangulation). Hence, each edge (vi, vj) is incident to exactly two faces. Thus,

MGM_GT ij = f X k=1 mikmjk = 2aij, whereAG = (aij)n×n.

Hence, we have proved thatMGMT

G =DG+ 2AG.

By a suitable labelling of vertices of G∇ andG_{, the adjacency matrices} _A₍_G∇_{) and} _A₍_G_{), and the}

diagonal matrices of vertex degreesD(G∇) andD(G_{) of}_G∇ _and_G _{have the following forms:}

(2.1) A(G∇) = _A G MG MT G 0f , A(G) = ₀ n MG MT G 0f , (2.2) D(G∇) = 2DG 0n×f 0f×n 3If , D(G) = DG 0n×f 0f×n 3If ,

whereAG, DG, andMG are the adjacency matrix, the diagonal matrix of vertex degrees, and the vertex-face incident matrix ofG, respectively, and 0n×f andIf are then×f matrix with all entries equal to zero and

the unit matrix of orderf. Hence, the Laplacian matricesL(G∇_{) and}_L₍_G_{) of}_G∇ _and_G _are

(2.3) L(G∇) = 2DG−AG −MG −M_GT 3If , L(G) = DG −MG −M_GT 3If .

Theorem 2.2. LetGbe a triangulation with nvertices andf faces embedded on an orientable surface, andG∇ _and_G _{the vertex-face graphs of the first kind and the second kind of} _G_{, respectively. Suppose the} normalized Laplacian spectrum ofGis {θ1, θ2, . . . , θn}. Then:

(1) The normalized Laplacian spectrum ofG∇ isn

f−n z }| { 1, . . . ,1,9+3θi± √ (9+3θi)2−120θi 12 , i= 1,2, . . . , n o .

(2) The normalized Laplacian spectrum ofG _isn

f−n z }| { 1,. . .,1,3± √ 9−6θi 3 , i= 1,2,. . ., n o . Proof.(1) Note that the normalized Laplacian characteristic polynomial ofGis

χ(G, x) = det xIn− LG = |xIn−DG−1/2LGDG−1/2| = |(x−1)In+DG−1/2AGDG−1/2| = |DG1/2||(x−1)In+DG−1AG||DG−1/2| = |xIn−(In−DG−1AG)|.

(4)

By equations (2.1) and (2.2), D(G∇)−1A(G∇) = 1 2DG −1_A G 1₂DG−1MG 1 3MG T ₀ f . Then χ(G∇, x) = det xIn+f−(In+f −D(G∇)−1A(G∇)) = det ₍_x₋₁₎_I n+1₂DG−1AG 1₂DG−1MG 1 3MG T ₍_x₋₁₎_If = (x−1)f_det (x−1)In+ 1 2DG −1_A G 1₂DG−1MG 1 3(x−1)MGT If ! = (x−1)f_det₍_x₋₁₎_In₊1 2DG −1_AG₋ 1 6(x−1)DG −1_MGMGT_. By Lemma 2.1,MGMT G =DG+ 2AG. Thus, χ(G∇_{, x}₎ ₌ ₍1 6) n₍_x₋₁₎f−n_{det 6(}_x₋₁₎2_I n+ 3(x−1)DG−1AG−DG−1(DG+ 2AG) = (1 6) n₍_x₋₁₎f−n_{det (6}_x2₋₉_x₎_I n−(3x−5) In−DG−1AG .

Note that the normalized Laplacian spectrum ofG(orAG) is{θ1, θ2, . . . , θn}. Then

χ(G∇, x) =1 6 n (x−1)f−n n Y i=1 6x2−9x−(3x−5)θi .

Thus, the zeros ofχ(G∇, x) are

f−n z }| { 1, . . . ,1,9 + 3θi± p (9 + 3θi)2−120θi 12 , i= 1,2, . . . , n. (2) Similarly, we can prove that the normalized Laplacian spectrum ofG is

n f−n z }| { 1, . . . ,1,3± √ 9−6θi 3 , i= 1,2, . . . , n o .

Theorem 2.3. LetGbe ak-regular triangulation withnvertices andf faces embedded on an orientable surface, and G∇ andG _{the vertex-face graphs of the first kind and the second kind of} _G_{, respectively. Let}

{λ1, λ2, . . . , λn} be the spectrum ofG. Then:

(1) The spectrum ofG∇ _isn f−n z }| { 0, . . . ,0,λi± √ λ2 i+8λi+4k 2 , i= 1,2, . . . , n o . (2) The spectrum ofG _isn f−n z }| { 0, . . . ,0,±√k+ 2λi, i= 1,2, . . . , n o .

(3) The Laplacian spectrum ofG∇ isn

f−n z }| { 3, . . . ,3,3+2k−λi± √ (3+2k−λi)2−20k+20λi 2 , i= 1,2, . . . , n o .

(4) The Laplacian spectrum ofG _isn

f−n z }| { 3, . . . ,3,3+k± √ (3+k)2₋_8k+8λ i 2 , i= 1,2, . . . , n o .

(5)

Proof.(1) By equation (2.1), the characteristic polynomial of G∇ is φ(G∇, x) = det xIn−AG −MG −MT G xIf = xf_det _xI n−AG −MG −1 xM T G If = xfdet xIn−AG−1 xMGM T G . By Lemma 2.1,MGMT

G =DG+ 2AG. SinceGisk-regular. Thus,

φ(G∇, x) = xf−n_det _x2_In₋_xAG₋_DG₋₂_AG

= xf−ndet (x2−k)In−(x+ 2)AG.

Note that the spectrum ofG(orAG) is{λ1, λ2, . . . , λn}. Then

φ(G∇, x) =xf−n n Y i=1 x2−k−(x+ 2)λi .

Thus, the zeros ofφ(G∇, x) are

f−n z }| { 0, . . . ,0,λi± p λ2 i + 8λi+ 4k 2 , i= 1,2, . . . , n. (2) Similarly, by equation (2.1), we can show that the spectrum ofG is

n f−n z }| {

0, . . . ,0,±pk+ 2λi, i= 1,2, . . . , no.

(3) By equation (2.3), the Laplacian characteristic polynomialµ(G∇, x) ofG∇is

µ(G∇, x) = det xIn−2DG+AG MG MT G (x−3)If . Hence, µ(G∇, x) = (x−3)f_det xIn−2DG+AG MG 1 x−3M T G If ! = (x−3)fdetxIn−2DG+AG− 1 x−3MGM T G .

SinceMGMGT =DG+ 2AG, and Gisk-regular,

µ(G∇, x) = (x−3)f−n_{det (}_x₍_x₋₃₎_In₋₂₍_x₋₃₎_DG_{+ (}_x₋₃₎_AG₋_DG₋₂_AG₎

= (x−3)f−n_{det (}_x2₋₃_x₎_In_{+ (5}₋₂_x₎_kIn_{+ (}_x₋₅₎_AG .

Note that the spectrum ofG(orAG) is{λ1, λ2, . . . , λn}. Thus,

µ(G∇, x) = (x−3)f−n n Y i=0 x2−3x+ (5−2x)k+ (x−5)λi.

(6)

Therefore, the zeros ofµ(G∇, x) are f−n z }| { 3, . . . ,3,3 + 2k−λi± p (3 + 2k−λi)2−20k+ 20λi 2 , i= 1,2, . . . , n.

(4) Similarly, we can prove that the Laplacian spectrum ofG _is

n f−n z }| { 3, . . . ,3,3 +k± p (3 +k)2₋₈_k_{+ 8}_λi 2 , i= 1,2, . . . , n o .

Remark 2.4. For thek-regular triangulations withn vertices andf faces embedded on an orientable

surface Σ with genusg, the three variablesk, gandnsatisfy the equation (k−6)n= 12(g−1), which shows that for fixed genusgnot equal to 1, there are only finitely many such triangulations. Only when the genus is 1 andk= 6, there are infinite families. For example, for anym≥2, n≥2, the triangular latticesTt₍_{n, m}₎

defined in Section 5 are 6-regular graphs on torus (i.e, genusg= 1).

3. Counting spanning trees of the vertex-face graphs. The enumeration of spanning trees of a graph G was first considered by Kirchhoff in the analysis of electric circuits [12]. It is a problem of fundamental interest in mathematics [1, 3, 18] and in physics [4, 16,19]. The number of spanning trees is closely related to the partition function of the q-state Potts model in statistical mechanics [9, 20]. Some recent studies on the enumeration of spanning trees and the calculation of their asymptotic growth constants on regular lattices were carried out in [4, 5,15,17]. We denote byt(G) the number of spanning trees of G. For convenience, we present a fundamental result about the normalized Laplacian spectrum and the number of spanning treest(G) of a graphG, for more details see [7].

Theorem 3.1. Let Gbe a connected graph with nverticesm edges, then the number of spanning trees of Gis (3.1) t(G) = 1 2m n Y i=1 di n Y k=2 θk,

wheredi is the degree of vertexvi of G, and the θk are the nonzero normalized Laplacian eigenvalue ofG.

For the notation above we have the following result.

Theorem 3.2. LetGbe a triangulation withnvertices andf faces embedded on an orientable surfaceΣ

with genusg, andG∇ andG _{the vertex-face graphs of the first kind and the second kind of} _G_{, respectively.} Then

t(G∇) = 3n+4g−35n−1t(G), t(G) = 3n+4g−32n−1t(G).

Proof. Note that G is a triangulation withn vertices and f faces, then |V(G∇)| =|V(G_)| ₌_n₊_f_,

m(G∇) =m+ 3f, m(G) = 3f, andmis the number of edges ofG. And 3f = 2m. Thus, (3.2) m(G∇) = 3m, m(G) = 2m.

Obviously, the degree sequences ofG∇andG _are_{2_d

1,2d2, . . . ,2dn, f z }| { 3, . . . ,3}and{d1, d2, . . . , dn, f z }| { 3, . . . ,3}.

(7)

By Theorem 2.2 and equations (3.1) and (3.2), we have t(G∇) = _2m(G1∇₎ n+f Q i=1 di(G∇) n+f Q k=2 θk(G∇) = 2n3f 6m n Q i=1 di 3 2×1 f−n Qn k=2 _9+3θ_k₊√_(9+3θ_k₎2₋_120θ_k 12 _9+3θ_k₋√_(9+3θ_k₎2₋_120θ_k 12 = 3f−n_2m+15n−1 n Q i=1 di n Q k=2 θk = 3f−n+1₅n−1_t₍_G₎_.

SinceGis a triangulation embedded on an orientable surface with genusg,n−m+f = 2−2gand 3f = 2m. Sof = 2n+ 4g−4. Hence,

t(G∇) = 3f−n+15n−1t(G) = 3n+4g−35n−1t(G).

Similarly, we can show thatt(G_{) = 3}n+4g−3₂n−1_t₍_G_).

By the theorem above, we have:

Corollary 3.3. Let Gbe a plane triangulation withn vertices. Then

t(G∇) = 3n−35n−1t(G), t(G) = 3n−32n−1t(G).

Corollary 3.4. Let Gbe a toroidal triangulation withn vertices. Then

t(G∇) = 3n+15n−1t(G), t(G) = 3n+12n−1t(G).

4. Kirchhoff index and degree-Kirchhoff index of vertex-face graphs. On the basis of electrical network theory, the study of resistance distance was initiated by Klein and Randi´c [13], and the related index, known as the Kirchoff index, is well studied in [10,21]. For any two verticesuandv in a connected graph

G, theresistance distanceΩ(u, v) betweenuandv is defined as the effective resistance betweenuandv by replacing each edge ofGwith unit resistors. TheKirchhoff indexof a graphG, denoted by Kf(G), is defined as the sum of resistance distances between all pairs of vertices [2,13]; that is,

Kf(G) = X {u,v}⊂V(G)

Ω(u, v).

At almost the same time, Gutman and Mohar [10] and Zhu et al. [23] proved that, ifGis a connected simple graph withnvertices, then

(4.1) Kf(G) =n n−1 X i=1 1 µi ,

whereµ1, µ2, . . . , µn−1 are the non-zero Laplacian eigenvalues ofG.

Recently, one modification of the Kirchhoff index, which takes the degrees of the graph into account, has been considered. The degree-Kirchhoff index is defined by Chen and Zhang [6]:

Kf0(G) = X {u,v}⊂V(G)

(8)

where du is the degree of the vertex uof G. They proved that, if G is a connected simple graph with n

verticesmedges, then

(4.2) Kf0(G) = 2m n X k=2 1 θk(G),

whereθ2, θ3, . . . , θn are the non-zero normalized Laplacian eigenvalues ofG.

Theorem 4.1. LetGbe a triangulation with nvertices andf faces embedded on an orientable surface, andG∇ _and_G _{the vertex-face graphs of the first kind and the second kind of}_G_{, respectively. Then}

Kf0(G∇) = 3f 5 (15f −6n+ 1) + 27 5 Kf 0 (G) and Kf0(G) = 3f(2f−2n+ 1) + 6Kf0(G).

Proof. Note that G is a triangulation withn vertices and f faces, then |V(G∇)| =|V(G_)| ₌_n₊_f_,

m(G∇) = m+ 3f, m(G_{) = 3}_f_{, where} _m _{is the number of edges of} _G_{. And 3}_f _{= 2}_m_{, then} _m₍_G∇_{) =} 3m, m(G) = 2m.

By Theorem 2.2 and equation (4.2), the degree-Kirchhoff index ofG∇is Kf0(G∇) = 2m(G∇) n+f P k=2 1 θk(G∇) = 6m (f−n) + 13 2 + n P k=2 12 9+3θk+ √ (9+3θk)2−120θk + 12 9+3θk− √ (9+3θk)2−120θk = 6m(f−n) + 4m+ 6m n P k=2 9 5θk + 3 5 = 3f₅ (15f −6n+ 1) + 27₅Kf0(G),

and the degree-Kirchhoff index ofG is

Kf0(G₎ ₌ ₂_m₍_G₎n+fP k=2 1 θk(G) = 4m (f−n) +1₂+ n P k=2 3 3+√9−6θk + 3 3−√9−6θk = 4m(f−n) + 2m+ 4m n P k=2 3 θk = 3f(2f −2n+ 1) + 6Kf0(G).

Theorem 4.2. LetGbe ak-regular triangulation withnvertices andf faces embedded on an orientable surface, andG∇ andG _{the vertex-face graphs of the first kind and the second kind of}_G_{, respectively. Then}

Kf(G∇) = f 2₋_n2 3 + n+f k+ 3 + (n+f)(n−1) 5 + (n+f)(k+ 3) 5n Kf(G) and Kf(G) =f 2₋_n2 3 + n+f k+ 3 + (n+f)(k+ 3) 2n Kf(G).

(9)

Proof. Suppose that the spectrum of G is{λ1, λ2, . . . , λn =k}. Then the Laplacian spectrum ofG is

{µ1=k−λ1, µ2=k−λ2, . . . , µn−1=k−λn−1, µn= 0}. By equation (4.1), the Kirchhoff index ofGis

Kf(G) =n n−1 X i=1 1 µi(G) =n n−1 X i=1 1 k−λi .

Note thatV(G∇) =V(G_{) =}_n₊_f_{. By Theorem 2.3, the Kirchhoff index of}_G∇ _is

(4.3) Kf(G∇) = (n+f) 1 3(f−n) + 1 k+3 + n−1 P i=1 1 µi(G∇) = 1₃(f2−n2) +n+f_k+3+(n+f) n−1 P i=1 2 3+2k−λi+ √ (3+2k−λi)2−20k+20λi + 2 3+2k−λi− √ (3+2k−λi)2−20k+20λi = f2−₃n2+n+f_k+3 +(n+f)(n₅ −1)+(n+f)(k+3)_5n Kf(G),

and the Kirchhoff index ofG _is

(4.4) Kf(G₎ ₌ ₍_n₊_f₎ 1 3(f−n) + 1 k+3+ n−1 P i=1 1 µi(G) = 1₃(f2₋_n2₎₊n+f k+3+(n+f) n−1 P i=1 2 3+k+ √ (3+k)2₋_8k+8λ_i+ 2 3+k−√(3+k)2₋_8k+8λ_i = f2−₃n2 +n+f_k+3 +(n+f)(k+3)_2n Kf(G).

5. Applications. As applications of the results in Section 2, 3 and 4, in this section we enumerate spanning trees of the dual lattice of the 3.12.12 lattice and the dice lattice with toroidal boundary condition in the context of statistical physics. We also obtain a formula of Kirchhoff indices of these two lattices.

The 3.12.12 lattice Rt(n, m) with toroidal boundary condition is shown in Figure 2(a). For any given vertex, the incident faces are list in, say, clockwise order, by the number of edges in the face, the list being the name of the lattice. Several lattices get multiple names, depending on the starting face, the convention is then to choose the lexicographically smallest name [14]. This is the origin of the name of the 3.12.12 lattice. ForRt(n, m) in Figure 2(a), allai’s,a∗_i’s,bi’s, andb∗_i’s are some vertices on the left, right, lower and upper boundaries, respectively, and the left and right (resp. the lower and upper) boundaries of the picture are identified such that (a1, a∗₁),(a2, a₂∗), . . . ,(am, a∗_m) and (b1, b₁∗),(b2, b∗₂), . . . ,(bn, b∗_n) are edges inRt₍_{n, m}_).

The 3.12.12 latticeRt(n, m) has been used by Fisher [8] in a dimer formulation of the Ising model.

The triangular lattice with toroidal boundary condition, denoted by Tt₍_{n, m}_{), can be regarded as an} n×msquare lattice with toroidal boundary condition with an additional diagonal edge added, in the same way, to every square, see Figure 2(b).

The dice lattice Dt₍_{n, m}_{) with toroidal boundary condition is the dual lattice of the kagom´}_{e lattice,}

depicted in Figure 2(c), which can be obtained from the hexagonal toroidal lattice by inserting a new vertex

vf to each facef and adding three edges vf, ui(f), whereu1(f), u2(f) andu3(f) are mutually non-adjacent vertices on the boundary off, such that two verticesvf1andvf2 have a common neighborui(f), i∈ {1,2,3}, wheref1, f2 are two adjacent faces.

(10)

1 2 i m a a a a 1 2 2 m-1 n-1

...

1 2 i m a a a a* * * * (

a

( (

b

( 1 2 i n b b b b 1 2 i n b* b* b* b* ... ... ... ... ... ... ... ... ... ... ... 1 1 2 2 i n-1 n n-1 i n 1 1 i i 2 2 m m m-1 m-1 a a a a a a a a a a b b b b b b b b b b * * * * * * * * * * a1 * 1 2 2 n-a2 ai a1 am a2 ai am * * * b1 b2 bi b1 b1 b2 bi b1 * * * * n-1 m-1 (

c

(

n-Figure 2. (a) The3.12.12latticeRt₍_{n, m}₎_{with toroidal boundary condition.} _{(b) The triangular lattice}_Tt₍_{n, m}₎_with

toroidal boundary condition. (c) The dice latticeDt₍_{n, m}₎_{with toroidal boundary condition.}

It is not difficult to see that the dual lattice of 3.12.12 latticeRt₍_{n, m}_{) and the dice lattice}_Dt₍_{n, m}_{) are}

the two vertex-face graphs of the triangular lattice Tt₍_{n, m}_{), that is,}_Rt₍_{n, m}₎⊥ ₌_Tt₍_{n, m}₎∇_, _Dt₍_{n, m}_{) =} Tt(n, m)_{. Note that the eigenvalues of}_Tt₍_{n, m}_{) [}₂₂_{] are}

(5.1) λij= 2 cos2πi

n + 2 cos 2πj m + 2 cos ₂_πi n + 2πj m , 0≤i≤n−1, 0≤j≤m−1.

Then, by Theorem 2.3, the spectra ofRt₍_{n, m}₎⊥ _and_Dt₍_{n, m}_{) are}    0mn, λij± q λ2 ij+ 8λij+ 24 2 ,0≤i≤n−1,0≤j≤m−1    and ( 0mn,± s 2 3+2 cos2πi n +2 cos 2πj m +2 cos ₂_πi n + 2πj m ,0≤i≤n−1,0≤j≤m−1 ) ,

respectively. The Laplacian spectra ofRt₍_{n, m}₎⊥ _and_Dt₍_{n, m}_{) are}    3mn, 15−λij± q λ2 ij−10λij+ 105 2 ,0≤i≤n−1,0≤j≤m−1    and    3mn,

9±q9+8 3+2 cos2πi_n +2 cos2πj_m +2 cos 2πi_n +2πj_m

2 ,0≤i≤n−1,0≤j≤m−1

 

 .

Shrock and Wu [15] showed that the number of spanning trees and the spanning tree entropy ofRt₍_{n, m}₎

can be expressed as (5.2) t(Rt(n, m)) = 75 mn n−1 Y i=0 m−1 Y j=0 (i,j)6=(0,0) 30 3−cos2πi m −cos 2πj n −cos ₂_πi m + 2πj n , and lim n,m→∞ 1 6mnlog[t(R t₍_{n, m}_))]

(11)

= 1 6log 30 + 1 24π2 Z 2π 0 Z 2π 0

log [6−2 cosx−2 cosy−2 cos (x+y)]dxdy≈0.7206,

and the number of spanning trees and the spanning tree entropy ofTt(n, m) can be expressed as

(5.3) t(Tt(n, m)) = 1 mn n−1 Y i=0 m−1 Y j=0 (i,j)6=(0,0) 6−2 cos2πi m −2 cos 2πj n −2 cos ₂_πi m + 2πj n , lim n,m→∞ log[t(Tt₍_{n, m}_))] nm = 1 4π2 Z 2π 0 Z 2π 0

log [6−2 cosx−2 cosy−2 cos (x+y)]dxdy≈1.6153.

Glasser and Wu [11] also derived the result above for the spanning tree entropy of the triangular lattice with toroidal boundary.

SinceRt₍_{n, m}₎⊥₌_Tt₍_{n, m}₎∇_,_Dt₍_{n, m}_{) =}_Tt₍_{n, m}₎_{. By Corollary 3.4 and equation (5.3), the following}

results are immediate.

Theorem 5.1. LetRt(n, m)be the 3.12.12 lattice with toroidal boundary condition. Then

t(Rt(n, m)⊥) = 3 mn+1₅mn−1 mn n−1 Y i=0 m−1 Y j=0 (i,j)6=(0,0) 6−2 cos2πi m −2 cos 2πj n −2 cos ₂_πi m + 2πj n .

Theorem 5.2. LetDt(n, m)be the dice lattice with toroidal boundary condition. Then

t(Dt(n, m)) = 3 mn+1₂mn−1 mn n−1 Y i=0 m−1 Y j=0 (i,j)6=(0,0) 6−2 cos2πi m −2 cos 2πj n −2 cos ₂_πi m + 2πj n .

By equation (5.2), a direct result of Theorem 5.1 is the following corollary.

Corollary 5.3. Let Rt(n, m)be the 3.12.12 lattice with toroidal boundary condition. Then

3t(Rt(n, m)) = 25t(Rt(n, m)⊥).

Remark 5.4. It is well known that a connected plane graphG and its dual graphG⊥ have the same

number of spanning trees. The corollary above implies that this is not true for graphs embedded on the torus.

Note that the triangular lattice with toroidal boundary conditionTt₍_{n, m}_{) is a 6-regular graph, which}

hasmnvertices and 2mnfaces. By equation (5.1), the Kirchoff index ofTt(n, m) is (5.4) Kf(Tt(n, m)) = mn 2 X 0≤i≤n−1 0≤j≤m−1 (i,j)6=(0,0) 1

3−cos2πi_n −cos2πj_m −cos(2πi_n +2πj_m)

(12)

Theorem 5.5. LetRt(n, m)be the 3.12.12 lattice with toroidal boundary condition. Then the Kirchhoff index ofRt₍_{n, m}₎⊥ _is Kf(Rt(n, m)⊥) = 8m 2_n2 5 − 4mn 15 + 27mn 10 X 0≤i≤n−1 0≤j≤m−1 (i,j)6=(0,0) 1 3−cos2πi n −cos 2πj m −cos 2πi n + 2πj m .

Theorem 5.6. Let Dt(n, m) be the dice lattice with toroidal boundary condition. Then the Kirchhoff index ofDt₍_{n, m}₎_is Kf (DL(m, n)) =m2n2+mn 3 + 27mn 4 X 0≤i≤n−1 0≤j≤m−1 (i,j)6=(0,0) 1

3−cos2πi_n −cos2πj_m −cos 2πi_n +2πj_m .

Acknowledgment. The authors are grateful to the anonymous referee and the editor for their careful reading and valuable comments which result in an improvement of the original manuscript. This work was supported by the National Natural Science Foundation of China (no. 11571139 and no. 11701324) and the Program for Outstanding Young Scientific Research Talents in Fujian Province University.

REFERENCES

[1] N.L. Biggs. Algebraic Graph Theory, second edition. Cambridge University Press, Cambridge, 1993.

[2] D. Bonchev, A.T. Balaban, X. Liu, and D.J. Klein. Molecular cyclicity and centricity of polycyclic graph: I. Cyclicty based on resistance distances or reciprocal distances.Int. J. Quantum Chem., 50:1–20, 1994.

[3] R. Burton and R. Pemantle. Local characteristics, entropy and limit theorems for spanning trees and domino tilings via transfer-impedances. Ann. Probab., 21:1329–1371, 1993.

[4] S.-C. Chang and R. Shrock. Some exact results for spanning trees on lattices.J. Phys. A: Math. Gen., 39:5653–5658, 2006. [5] S.-C. Chang and W. Wang. Spanning trees on lattices and integral identities. J. Phys. A: Math. Gen., 39:10263–10275,

2006.

[6] H.Y. Chen and F.J. Zhang. Resistance distance and the normalized Laplacian spectrum. Discrete Math., 155:654–661, 2007.

[7] F.R.K. Chung. Spectral Graph Theory. American Mathematical Society, Providence, 1997. [8] M.E. Fisher. On the dimer solution of planar Ising models. J. Math. Phys., 7:1776–1781, 1996.

[9] C.M. Fortuin and P.W. Kasteleyn. On the random cluster model. I. Introduction and relation to other models. Physica, 57:536–564, 1972.

[10] I. Gutman and B. Mohar. The quasi-Wiener and the Kirchhoff indices coincide.J. Chem. Inf. Comput. Sci., 36:982–985, 1996.

[11] M.L. Glasser and F.-Y. Wu. On the entropy of spanning trees on a large triangular lattice. The Ramanujian Journal, 10:205–214, 2005.

[12] G. Kirchhoff. Über die Auflösung der Gleichungen, auf welche man bei der Untersuchung der linearen Verteilung galvanis-cher Ströme geführt wird. Ann. Phys. Chem., 72:497–508, 1847.

[13] D.J. Klein and M. Randi´c. Resistance distance. J. Math. Chem., 12:81–95, 1993.

[14] R. Parviainen. Connectivity Properties of Archimedean and Laves Lattices. Doctoral dissertation, Department of Mathe-matics, Uppsala University, 2004.

[15] R. Shrock and F.-Y. Wu. Spanning trees on graphs and lattices inddimensions. J. Phys. A: Math. Gen., 33:3881–3902, 2000.

[16] H.N.V. Temperley. The enumeration of graphs on large periodic lattices. In: D.J.A. Welsh and D.R. Woodall (editors),

Combinatorics: Proc. Combinatorial Mathematics, The Institute of Mathematics and its Applications, Oxford, 356–

357, 1972.

[17] W.-J. Tzeng and F.-Y.Wu. Spanning trees on hypercubic lattices and nonorientable surfaces.Appl. Math. Lett., 13:19–25, 2000.

(13)

[18] D.J.A. Welsh. Complexity: Knots, Colourings, and Counting. London Math. Soc. Lecture Notes Series, Vol. 186, Cam-bridge University Press, CamCam-bridge, 1993.

[19] F.-Y. Wu. Number of spanning trees on a lattice.J. Phys. A: Math. Gen., 10:L113–L115, 1977. [20] F.-Y. Wu. The Potts model.Rev. Mod. Phys., 54:235–268, 1982.

[21] J.W. Xiao and I. Gutman. Resistance distance and Laplacian spectrum.Theor. Chem. Acc., 110:284–289, 2003. [22] W.G. Yan and Z.H. Zhang. Asymptotic energy of lattices. Physica A, 388:1463–1471, 2009.