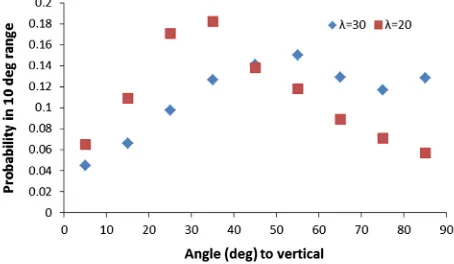
Discrete element modelling of flexible fibre packing
Full text
Figure


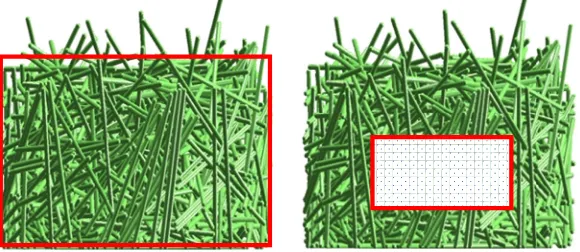
![Fig. 4. Snapshots of DEM Sphero-cylinder fill and packing [9].](https://thumb-us.123doks.com/thumbv2/123dok_us/8674410.377342/4.595.50.286.337.551/fig-snapshots-of-sphero-cylinder-ll-and-packing.webp)
Related documents
We compare the performance of Exhaustive-IGain to MBS-IGain using 10 simulated 40-predictor datasets based on 5 interactions with marginal effects, 16 simu- lated 40-predictor
In the bivariate analysis, sex, profession, service year, availability of water for hand washing in the healthcare worker’s ward or department, the presence of an infec- tion
Also, the process variation-aware Load Balance of Multiple Paths (LBMP) transistor sizing algorithm presented is an attempt to realize an efficient scheme to
One hypothesis concerning the different trends in educational differentials in the two countries during the 1980s is that relatively more rapid growth in the supply of more
This literature review aims at identifying and examining the risk factors for WPV; the psychological and physical effects experienced by nurses due to WPV; the strategies
The United States Court of Appeals for the Tenth Circuit reversed and HELD: The clause in question did not operate as a waiver of defenses under Section 9-206(1)
On the basis of summarizing the cloud security’s characteristics, superiority and core technologies, this paper proposes a new method to design and realize intelligent IPS model
UNIVERSITI PUTRA MALAYSIA PHOTOVOLTAIC-BASED SINGLE-ENDED PRIMARY-INDUCTOR CONVERTER WITH DUAL-FUZZY LOGIC CONTROL-BASED MAXIMUM POWER POINT TRACKING... PHOTOVOLTAIC-BASED