Vanadium(V) oxide arsenate(V), VOAsO4
Full text
Figure
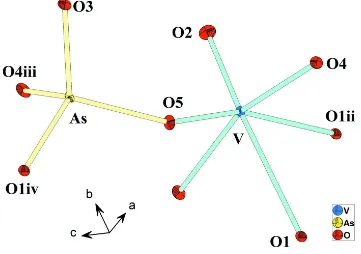
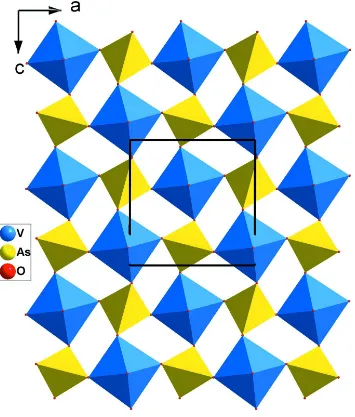
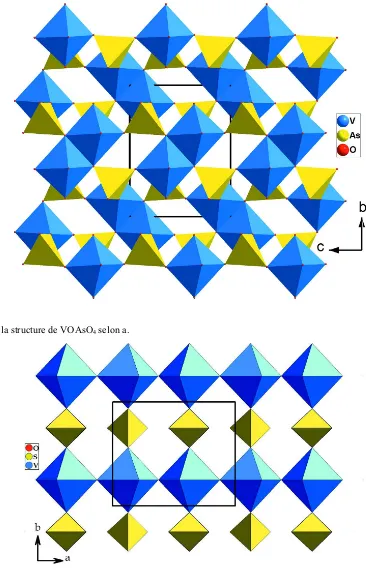
Related documents
• Bagian dalam dan luar dari standar (tiang) dihubungkan dengan dengan transoms.. • Transoms umumnya dihubungkan dengan dengan standar di
Etymology : named after its association with relatively small lesion spots. Simile ut Teratosphaeria gauchensis , sed differret absentia conidiophororum. Leaf spots epiphyllous
12) Should Bolton at home conduct free maintenance for tenants if they are socially deprived, even if they must bare the cost for the repair?. Yes
Although the paper is not marked by a cross in the Yes voting box, it clearly indicates the voter’s intention to choose the “Yes” option, and so it is a good vote for Yes
This study has addressed two research questions regarding the manifestation of rhetorical moves along with their constituent steps and the manifestation of the rhetorical
The results of the present study regarding the role of grade in problem solving performance of students showed that the performance of first grade students of junior high
This study focuses on the use of lexical bundles (LBs), their structural forms, and their functional classifications in journal articles of four academic
The students of all majors need to have enough English knowledge to get their needed information from these sources, whereas large amount of academic courses around the world