Enumeration of disjoint Hamilton cycles in a divisor Cayley graph

(1)

https://doi.org/10.26637/MJM0603/0006

Enumeration of disjoint Hamilton cycles in a divisor

Cayley graph

Levaku Madhavi

1

and Tekuri Chalapathi

2*

Abstract

Hamilton cycles are cycles of largest length and triangles are cycles of smallest length in a graph. In this paper an enumeration method of determining the number of disjoint Hamilton cycles in the Divisor Cayley graph associated with the arithmetical function, namely the divisor functiond(n),n≥1is presented.

Keywords

Hamilton cycle, Outer Hamilton cycle, Symmetric set, Cayley graph, Divisor Cayley graph.

AMS Subject Classification

68R10, 05C30, 05C45.

1_{Department of Applied Mathematics, Yogi Vemana University, Kadapa-516003, A.P., India,} 2_{Department of Mathematics, Sree Vidyanikethan Engineering College, Tirupati-517502, A.P., India.}

*Corresponding author:1_{lmadhaviyvu@gmail.com;} 2_{chalapathi.tekuri@gmail.com}

Article History: Received21March2018; Accepted30May2018 2018 MJM.c

1. Introduction

In 1980 Nathanson [11] introduced the concept of Congru-ences in Number Theory into Graph Theory and thus paved the way for the emergence of a new class of graphs called Arithmetic Graphs. According to him an arithmetic graph is a simple graph whose vertex set isV={1,2, ...,n}, the set of firstnpositive integers and two verticesxandyare adjacent if and only ifx+y≡z(modn) wherez∈S, a pre-assigned subset ofV. Later many researchers [5,12,14] followed this trend and studied arithmetical graphs associated with various arithmetical functions.

There is another class of graphs, called Cayley graphs. A Cayley graph is the graph whose vertex setV is the set of elements of a finite group(X,·)and two verticesxandyare adjacent if and only ifx−1y, or,y−1xare in some symmetric subsetSofX(a subsetSof a group(X,·)is called a symmetric

subset ofXifs−1is inSfor alls∈S). This Cayley graph is

denoted byG(X,S)and|S|- regular and contains |X||S| 2 edges (see pp 15-16, [8] ).

The cycle structure of Cayley graphs and Unitary Cayley graphs were studied by Berrizbeitia and Guidici [1,2] and Detzer and Guidici [6]. Recently Maheswari and Madhavi [8– 10] studied the enumeration methods for finding the number of triangles and Hamilton cycles in arithmetic graphs associated with the quadratic residues modulo a primepand the Euler totient functionϕ(n),n≥1 an integer. In [4] Chalapathi et al. gave a method of enumeration of triangles in the arithmetic Cayley graph, namely the divisor Cayley graph associated with the divisor functiond(n),n≥1 an integer. The main aim of this paper is to give an enumeration process for counting the number of disjoint Hamilton cycles in the divisor Cayley graph. In this study we have followed Bondy and Murty [3] for graph theory and Apostol [13] for number theory terminology.

2. The Divisor Cayley Graph and its

Properties

(2)

divisor Cayley graph G(Zn,D∗)is the Cayley graph asso-ciated with the group(Zn,⊕)and its symmetric subset D∗. That is the graph G(Zn,D∗)is the graph whose vertex set is Zn={0,1,2, ...,n−1}and the edge set is E={(x,y):either x−y or y−x is in D∗_}.

In [4] it is established thatG(Zn,D∗)is|D∗|-regular with

sizen|D

∗_|

2 , connected and the degree of each vertex inG(Zn,D

∗₎

is odd (even) if and only ifnis even(odd). Further, it is not bipartite and Eulerian if and only ifnis odd.

Lemma 2.2. The graph G(Zn,D∗)is Hamiltonian.

Proof. For 0≤i≤n−1, (i+1)−i=1 and 1∈D∗since 1 dividesn trivially. Soi and i+1 are adjacent and thus

(0,1,2, ...,n−1,0)is a cycle of lengthnwhich is a Hamilton cycle inG(Zn,D∗)so thatG(Zn,D∗)is Hamiltonian.

Definition 2.3. The cycle(0,1,2, ...,n−1,0)is called the

outer Hamilton cycleof the graph G(Z_n,D∗).

Lemma 2.4. If n is a prime then the graph G(Z_n,D∗)is the outer Hamilton cycle.

Proof. Suppose thatnis a prime. Then 1 is the only divisor ofnother thannso thatD∗={1,n−1}. Hence the graph

G(Zn,D∗)is 2-regular and the only edges inG(Zn,D∗)are (i,i+1)for 0≤i≤n−1 so thatG(Zn,D∗)is the outer

Hamil-ton cycle.

Lemma 2.5. Let n≥1be an integer and d6=n be a divisor of n. Then G(Z_n,D∗)contains exactly d disjoint cycles each

of length n d.

Proof. Letd be a divisor ofnand letk=n

d.For 1≤i≤k, (i+1)d−id=d∈D∗ so that (i,i+1)is an edge. Also

kd= (n

d)d=n=0. So C0= (0,d,2d, ...,kd=0)

is a cycle of lengthkinG(Zn,D∗). Similarly one can see C1= (1,d+1,2d+1, ...,kd+1=1),

C2= (2,d+2,2d+2, ...,kd+2=2),

...,

Cd−1= (d−1,d+ (d−1),2d+ (d−1), ...,kd+ (d−1) =

d−1)

are also cycles of lengthk. Further no two of these cycles have a vertex in common so that they are disjoint cycles. Moreover the vertex set ofC0∪C1∪C2∪...∪Cd−1is equal to the vertex

set ofG. Hence corresponding to each divisordofnthere are

ddisjoint cycles, each of lengthk(= n

d)inG(Zn,D ∗₎_.

Remark 2.6. For any divisor d of n the d disjoint cycles C0,C1,C2, ...,Cd−1are referred to as the cycles corresponding

to the divisor d. These cycles play a crucial role in determin-ing the edge disjoint Hamilton cycles in the divisor Cayley graph G(Zn,D∗).

3. Enumeration of disjoint Hamilton

cycles in a Divisor Cayley graph

Definition 3.1. Hamilton cycles H1and H2are said to be

edge disjoint if the edge sets E(H1)and(H2)are disjoint.

Theorem 3.2. If n is even then the graph G(Zn,D∗)cannot be decomposed intoedge disjointHamilton cycles.

Proof. Let n≥1 be an even integer. Then by part (a) of Lemma 2.4 of [4] the degreeqof each vertex is odd and the number of edges inG(Zn,D∗)is

nq

2 . IfG(Zn,D

∗₎_is

decom-posed into the union ofkdisjoint Hamilton cycles (since each Hamilton cycle containsnedges) then the number of edges inG(Zn,D∗)isnkso thatnk=nq

2 , or, k=

q

2. This is not

possible sinceqis odd. SoG(Zn,D∗)cannot be decomposed

into edge disjoint Hamilton cycles.

Theorem 3.3. The graph G(Zn,D∗)can be decomposed into edge disjoint Hamilton cycles if, and only if, n is odd.

Proof. First suppose that the graphG(Zn,D∗)is a union ofk

number of edge disjoint Hamilton cycles, sayH1,H2, ...,Hk.

Since eachHi, 1≤i≤kcontainsnedges the number of edges

inG(Zn,D∗)iskn. IfG(Zn,D∗)isr- regular then the number

of edges inG(Zn,D∗)is also equal to rn

2 so that

nr

2 =nk. This givesr=2kso thatris even. That is, each vertex of

G(Zn,D∗)is of even degree so thatnis odd.

Conversely assume thatnis odd. Adopting the following procedure all the edge disjoint Hamilton cycles ofG(Zn,D∗)

can be found. Letd1>d2> ... >dmbe divisors ofnother than

1 andn. Thendi’s are also odd. Choose the outer Hamilton

cycleH0= (0,1,2, ...,n−1,0)and consider thed disjoint

cyclesC0,C1,C2, ...,Cd−1corresponding to the divisord=d1.

Each of theCi’ s is edge disjoint withH0. Let the spanning

subgraphC0=C0∪C1∪C2∪...∪Cd−1.

Using the following procedure indstages in which a pair of edges are deleted in each stage fromH0and adjoined to

the spanning sub graphC0and on the other hand a pair of

edges are deleted fromC0 and adjoined toH0and H0 is

transformed into a Hamilton cycleH1while the cycles inC0

are merged into a Hamilton cycleC1. More specifically at the

ithstage

(i) the edges(i−1,1),(d+ (i−1),d+i)are deleted from

H012...i−1and these are adjoined toC012...i−1and the edges

(i−1,d+ (i−1))and(i,d+i)are deleted fromC012...i−1and

these adjoined toH012...i−1to getH012...iandC012...iifiis odd

and

(ii) the edges(i−1,i),((i−1)+d−1_,_i_+d−1₎_{are deleted from}

H012...i−1and these are adjoined toC012...i−1and the edges

(i−1,(i−1) +d−1),(i,i+d−1)are deleted fromC012...i−1

and these are adjoined toH012...i−1to getH012...iandC012...i ifiis even. Hered−1is the inverse ofdin(Zn,⊕)andd−1=

(3)

We repeat this process by taking the divisord2in place of

d1and the Hamilton cycleC1in place of the outer Hamilton

cycleH0and the union of disjoint cycles corresponding to

d2in place ofC0and obtain a Hamilton cycleH2=H0123...d2

fromC2and a Hamilton cycleC2=C0123...d2 by merging the d2disjoint cycles corresponding to the divisord2. Applying

this procedure for all the divisors ofn other than 1 and n

we obtain the required disjoint Hamilton cycles ofG(Zn,D∗).

This procedure is illustrated for a divisordin step 1. Step 1:Choose the outer Hamilton cycleH0= (0,1,2, ...,n−

1,0)and the divisord(=d1)ofn. Let us take its complement

HC

0 ofH0and the spanning sub graphC0that contains all

disjoint cyclesC0,C1,C2, ...,Cd−1generated by the divisord

inH₀C. It is easy to observe that the vertices 0,1,2, ...,(d−1)

lie in distinct cycles that are generated byd.

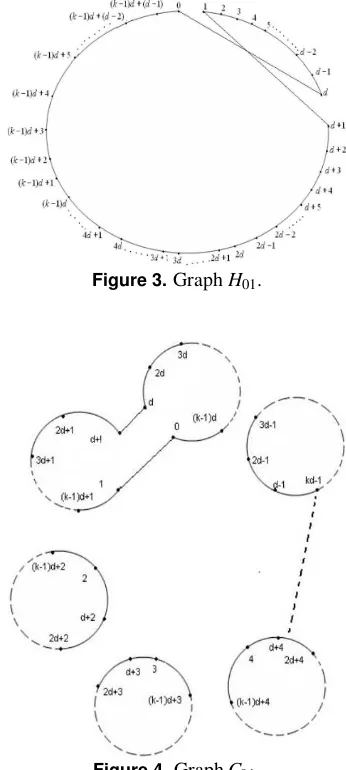
Figure 1.GraphH0.

Figure 2.GraphC0.

Using the procedure outlined above indstages we construct a pair of Hamilton cycles, one fromH0and the other by

merg-ing the cyclesC0,C1,C2, ...,Cd−1in the following way.

Stage 1:Delete the edges(0,1),(d,1+d)fromH0and

ad-join these toC0and delete the edges(0,d),(1,1+d)from

C0 and adjoin to H0. By this H0 transforms into H01=

(0,d,d−1,d−2, ...,3,2,1,d+1,d+2, ...,(k−1)d+ (d−

1),1,0)which is aHamilton cycleandC0transforms into

C01, which is a union of the disjoint cyclesC1,C2, ...,Cd−1,

whereC1= (0,(k−1)d,(k−2)d, ...,3d,2d,d,d+1,2d+1, ...,

(k−1)d+1,1,0), which is the cycle got by merging the first two cyclesC0andC1inC0, by the construction it is clear that

H01andC01are disjoint.

Stage 2:Delete the edges(1,2)and(1+ (k−1)d,2+ (k−

1)d)fromH01 and adjoin these edges toC01and delete the

edges(1,1+ (k−1)d)and(2,2+ (k−1)d)from andC01

adjoin these edges toH01. By thisH01transforms intoH012

which isthe disjoint union of the two cycles(0,d,d−1, ...,2,

(k−1)d+2,(k−1)d+3, ...,(k−1)d+d−1,0)and(1,d+

1,d+2, ...,(k−1)d,(k−1)d+1,1) whileC01 transforms

intoC012 which is the disjoint union ofC2,C3,C4, ...,Cd−1,

whereC2= (0,(k−1)d,(k−1)d−1, ...,3d,2d,d,d+1,2d+

1, ...,(k−1)d+1,(k−1)d+2, ...,2d+2,d+2,2,1,0). By the construction it is clear thatH012andC012are disjoint.

Observe that starting with Hamilton cycleH0this process

afterith_{stage transforms the Hamilton cycle}_H

(4)

(i) a Hamilton cycleH0123...iifiisoddand

(ii) a subgraphH0123...iwhich is a union of two disjoint cycles

ifiiseven.

Repeating this process successively d times the outer Hamilton cycleH0transforms into theHamilton cycle(since

dis odd)

H012...d= (0,d,2d, ...,3d,3d+1, ...,4d,4d+1, ...,(k−1)d,(k −1)d+1,1,d+1,d+2,2,(k−1)d+2,(k−1)d+3,3,d+

3,d+4,4,(k−1)d+5,5,d+5, ...,2d−2,2d−1,d−1,(k−

1)d+ (d−1),0)

and the subgraphC0is transformed into the Hamilton cycle

(which is got by merging the cyclesC0,C1, ...,Cd−1)

C012...d= (0,(k−1)d, ...,3d,2d,2d−1,3d−1,(k−1)d−1, kd−1,(k−1)d+ (d−2), ...,(k−1)d+5, ...,d+4,2d+4, ...,

(k−1)d+4,(k−1)d+3, ...,2d+3,d+3,d+2,2d+2, ...,(k −1)d+2,(k−1)d+1, ...,3d+1,2d+1,d+1,d,d−1,d−

2, ...,5,4,3,2,1,0).

Let us takeH012...d=H1andC012...d=C1. The

construc-tion of the Hamilton cyclesH1andC1shows that they are

edge disjoint. The following edges ofH1are transmitted to

C1.

(i)(0,1),(1,2),(2,3), ...,(d1−1,d1)

Figure 7.GraphH012...d=H1.

Figure 8.GraphC012...d=C1.

(ii)(d1,d1+1),(d1+2,d1+3), ...,(2d1−1,2d1)(sinced+

d−1=2d−1 andd+d=2d)

(iii)(n−d1+1,n−d1+2),(n−d1+3,n−d1+4), ...,(n−

2,n−1)(since(n−d) +d−2=n−2 and(n−d) +d−1= n−1).

Step 2:Let us takeC1in place ofH0and the spanning

sub-graph consisting of all cycles generated by the divisord2in

the complementC₁cofC1. Sinced1andd2are also odd,d2≤

d1−2. Hence the set as edges{(0,1), ...,(d2−1,d2)}belong

to the set of edges given in (i). Moreover,d1,d1+2,2d1−

1;n−d1+1,n−d1+3, ... are all odd and d2<d1 so that

the set of all edges{(d2,d2+1),(d2+2,d2+3), ...,(2d2−

1,2d2),(n−d2+1,n−d2+2), ...,(n−2,n−1)} belong to

the set of all edges given in (ii) and (iii).

Repeating the procedure given in step1 withd2in place

ofd1 one obtains the Hamilton cycles H012...d2 =H2 and C012...d2=C2. From the construction ofH1,H2andC2it is

clear that they are mutually edge disjoint.

Repeating the same procedure as in the step 1 and step 2 for the divisorsd3,d4, ...,dm, one gets edge disjoint

Hamil-ton cyclesH3,H4, ...,HmandHm+1=Cmwhich are edge

(5)

Further eachHi, 1≤i≤m+1 being Hamiltonian con-tains exactlynedges. So the number of edges inH1∪H2∪

...∪Hm+1is equal ton(m+1).

Alsod1,d2, ...,dm,1 are the only divisors ofnother than

n.So

D∗={d1,d2, ...,dm,1,n−d1,n−d2, ...,n−dm,n−1}

and|D∗_|₌₂_(m₊₁₎_{. Since}_G(Z

n,D∗)is|D∗|- regular and the

number of edges ofG(Z_n,D∗)is n|D

∗_|

2 , or,n(m+1), which is equal to the number of edges in H1∪H2∪...∪Hm+1.

ThusG(Zn,D∗) is a disjoint union of the Hamilton cycles H1,H2, ...,Hm+1.

The following corollary is immediate from the Theorem 3.3.

Corollary 3.4. If n≥1is an odd integer then G(Zn,D∗)has m+1 disjoint Hamilton cycles, where m is the number of divisors of n other than1and n.

Corollary 3.5. If n≥1is an odd integer then the number of edge disjoint Hamilton cycles of G(Zn,D∗)is d(n)−1, where d(n)is the number divisors of n.

Proof. For any odd positive integern≥1, the divisor function

d(n)denotes the number of divisors including 1 andn. By the Corollary 3.4 the number of disjoint Hamilton cycles in

G(Zn,D∗)ism+1 wheremis the number of divisors ofn

other than 1 andn. Som=d(n)−2 and the number of disjoint Hamilton cycles ofG(Zn,D∗)isd(n)−1.

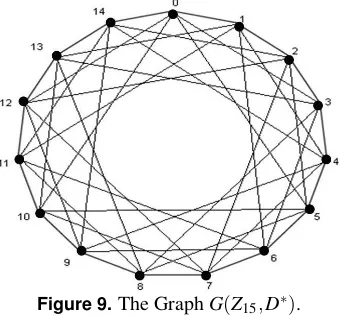
Example 3.6. For the divisor Cayley graph the G(Z15,D∗)let

us enumerate the edge disjoint Hamilton cycles. The divisors of15other than15are1,3and5. So D={1,3,5}and D∗= {1,3,5,10,12,14}. The graph of G(Z₁₅,D∗)is as follows.

Figure 9.The GraphG(Z₁₅,D∗).

Step 1:For the divisor d=5, the5disjoint cycles of length

3are(0,5,10,0),(1,6,11,1),(2,7,12,2),(3,8,13,3)and (4,9,14,4).

The outer Hamilton cycleH0and the spanning sub graph

C0which is the union of the above5cycles are as follows.

(i) Deleting the edges(0,1),(5,6)from H0 and adjoining

these toC0and deleting the edges(0,5),(1,6)fromC0and

Figure 10.The Graphs ofH0andC0respectively.

adjoining these toH0,H0transforms into the Hamilton

cy-cle H01= (1,2,3,4,5,0,14,13,12,11,10,9,8,7,6,1)andC0

into the subgraph C01= (0,1,11,6,5,10,0)∪(3,13,8,3)∪

(2,7,12,2)∪(4,9,14,4).

(ii) Deleting the edges(1,2),(11,12)from H01 and

adjoin-ing them to C01 and deleting the edges(1,11),(2,12)from

C01and adjoining them to H01, H01transforms into H012=

(1,11,10,9,8,7,1)∪(2,3,4,5,0,14,13,12,2)and C01

trans-forms into C012= (0,1,2,7,12,11,6,5,10,0)∪(3,8,13,3)∪

(4,9,14,4).

(iii) Deleting the edges(2,3),(7,8)from H012and adjoining

to C012and the Hamilton cycle deleting the edges(2,7),(3,8)

from C012and adjoining them to H012, H012transforms into

H0123= (0,5,4,3,8,9,10,11,1,6,7,2,12,13,14,0) and the

subgraph C0123= (0,1,2,3,13,8,7,12,11,6,5,10,0)∪(4,9,

14,4).

(iv) Deleting the edges(3,4),(13,14)from H0123and

(6)

C0123 and adjoining them to H0123, H0123 transforms into

H01234= (0,5,4,14,0)∪(1,6,7,2,12,13,3,8,9,10,11,1)and

the subgraph C0123into C01234= (0,1,2,3,4,9,14,13,8,7,12,

11,6,5,10,0).

(v) Deleting the edges(4,5),(9,10)from H01234and

adjoin-ing them to C01234and deleting the edges(4,9),(5,10)from

C01234and adjoining them to H01234, H01234transforms into

the Hamilton cycle H012345= (0,5,10,11,1,6,7,2,12,13,

3,8,9,4,14,0)and the subgraph C01234into C012345= (0,1,2,

3,4,5,6,11,12,7,8,13,9,10,0). We take H₀₁₂₃₄₅=H₁and C012345=C1.

Figure 15.The Hamilton cyclesH1andC1respectively.

Step 2:Let us take the divisor3of15in place of the divisor5

and the Hamilton cycleC1in place of the outer Hamilton cycle

H0. Consider the subgraphC

0

0consisting of the disjoint

cy-cles generated by the divisor5in the complimentC₁c. That is C0

0= (0,3,6,9,12,0)∪(1,4,7,10,13,1)∪(2,5,8,11,14,2)

corresponding to the divisor3of15are as follows.

Let us apply the procedure enumerated in step 1 toC1andC

0

in the following three stages.

(i) Deleting the edges(0,1),(3,4)fromC1and adjoining to

Figure 16.The Graphs ofC1andC

0

0respectively.

C0

0and deleting the edges(0,3),(1,4)fromC

0

0and adjoining

these toC1,C1transforms into H

0

01= (0,3,2,1,4,5,6,11,12,7,

8,13,14,9,0)andC₀0into the subgraph C₀₁0 = (0,1,13,10,7,4 ,3,6,9,12,0)∪(2,5,8,11,14,2).

(ii) Deleting the edges(1,2),(13,14)from H₀₁0 and adjoin-ing them to C₀₁0 and deleting the edges(1,13),(2,14)from C0₀₁and adjoining them to H₀₁0 , H₀₁0 transform into H₀₁₂0 = (0,3,2,14,9,10,0)∪(1,4,5,6,11,12,7,8,13,1)and C₀₁0 into C1₀₁₂= (0,1,2,5,8,11,14,13,10,7,4,3,6,9,12,0).

(iii) Deleting the edges(2,3),(5,6)from H₀₁₂0 and adjoining them to C₀₁₂0 and deleting the edges(2,5),(3,6)from C0₀₁₂and adjoining them to H₀₁₂0 , H₀₁₂0 transforms into the Hamilton cy-cle H₀₁₂₃0 = (0,3,6,11,12,7,8,13,1,14,5,2,14,9,10,0)and C0₀₁₂₃into the Hamilton cycle C0₀₁₂₃= (0,1,2,3,4,7,10,13,14, 11,8,5,6,9,12,0). We denote H₀₁₂₃0 =H₂and C0₀₁₂₃=H₃.

Figure 17.The Hamilton cyclesH2andH3respectively.

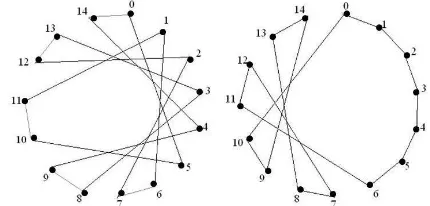
Thus the three edge disjoint Hamilton cycles of the divisor Caley graph G(Z15,D∗)areH1,H2andH3given in Figure

18.

4. Conclusion

(7)

Figure 18.The Hamilton cyclesH1,H2andH3

respectively.

5. Acknowledgement

The authors express their thanks to Prof. L. Nagamuni Reddy for his suggestions during the preparation of this paper.

References

[1] _{P. Berrizbeitia and R. E. Giudici, Counting Pure k-cycles}

in Sequences of Cayley graphs,Discrete Mathematics, 149(1996), 11-18.

[2] _{P. Berrizbeitia and R. E. Giudici, On cycles in the}

Se-quence of Unitary Cayley graphs. Reporte Techico No.01-95, Universidad Simon Bolivar, Dpto. de Matahematicas, Caracas, Venezula,(1995).

[3] _{J. A. Bondy and U. S. R. Murty, Graph Theory with}

Applications,Macmillan, London, (1976).

[4] _{T. Chalapathi, L. Madhavi and S. Venkata Ramana,}

Enu-meration of Triangles in a Divisor Cayley graph,Momona Ethiopian Journal of Science, 5(2013), 163-173. [5] _{G. Chartrand, R. Muntean, V. Saenpholphat and P. Zhang,}

Which graphs are divisor graphs?, Proceedings of the Thirty-second Southeastern International Conference on Combinatorics, Graph Theory and Computing, Baton Rouge, LA, Congr. Numer., 151 (2001), 189-200. [6] _{I. Dejter and R. E. Giudici, On Unitary Cayley graphs,}

JCMCC, 18(1995), 121-124.

[7] _{L. Madhavi and T.Chalapathi, Enumeration of Triangles}

in Cayley Graphs,Pure and Applied Mathematics Jour-nal, 4(2015), 128-132.

[8] _{L. Madhavi, Studies on Domination Parameters and}

Enu-meration of Cycles in some Arithmetic Graphs, Doc-toral Thesis, Sri Venkateswara University, Tirupati, India, (2002).

[9] _{B. Maheswari and L. Madhavi, Enumeration of Triangles}

and Hamilton Cycles in Quadratic Residue Cayley graphs,

Chamchuri Journal of Mathematics, 1(2009), 95-103. [10] _{B. Maheswari and L. Madhavi, Enumeration of}

Hamil-ton Cycles and Triangles in Euler totient Cayley graphs,

Graph Theory Notes of New York LIX, (2010), 28-31. [11] _{M. B. Nathanson, Connected Components of arithmetic}

graphs,Monatshefte f¨ur Mathematik, 29(1980), 219-220. [12] _{G. S. Singh and G. Santosh, Divisor Graphs – I, Preprint,}

(2000).

[13] _{T. M. Apostol, Introduction to Analytic Number Theory,}

Springer International, Student Edition (1989).

[14] _{T. Yu-Ping, A simple research of divisor graphs,}_{The 29th}

Workshop on Combinatorial Mathematics and Computa-tion theory,(2012) 186-190.

? ? ? ? ? ? ? ? ? ISSN(P):2319−3786 Malaya Journal of Matematik

Enumeration of disjoint Hamilton cycles in a divisor Cayley graph