Generalized Mathematical Model for Biological Growths
Purnachandra Rao Koya, Ayele Taye Goshu*
School of Mathematical and Statistical Sciences, Hawassa University, Hawassa, Ethiopia Email: drkpraocecc@yahoo.co.in, *ayele_taye@yahoo.com
Received June 11,2013; revised July 15, 2013; accepted August 1, 2013
Copyright © 2013 Purnachandra Rao Koya, Ayele Taye Goshu. This is an open access article distributed under the Creative Com-mons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
In this paper, we present a generalization of the commonly used growth models. We introduce Koya-Goshu biological growth model, as a more general solution of the rate-state ordinary differential equation. It is shown that the commonly used growth models such as Brody, Von Bertalanffy, Richards, Weibull, Monomolecular, Mitscherlich, Gompertz, Lo-gistic, and generalized Logistic functions are its special cases. We have constructed growth and relative growth func-tions as solufunc-tions of the rate-state equation. The generalized growth function is the most flexible so that it can be useful in model selection problems. It is also capable of generating new useful models that have never been used so far. The function incorporates two parameters with one influencing growth pattern and the other influencing asymptotic behav-iors. The relationships among these growth models are studies in details and provided in a flow chart.
Keywords: Growth Model; Koya-Goshu Function; Gompertz, Logistic; Richards; Weibull
1. Introduction
Measuring biological growth has been important in many fields. Many researchers have contributed in developing relevant models: [1] for Brody function; [2] for Von Bertalanffy function; [3,4] for Richards function; [5] for Gompertz function; [6-8] for Logistic function; [6,9-11] for Generalized Logistic; [12,13] for Weibull function; [1,14] for Monomolecular function.
The mathematical representation of the relative growth is described by the ordinary differential equation (ODE) or rate-state equation
dd t
f t
r f t
t (1) Here f t
is representing growth function and t isrelative rate function at time . This ordinary differen-tial equation has many solutions among which some are studied in this paper. The growth models have been widely used in many biological growth problems includ-ing: in animal sciences [1,5,7,8,15,16] and in forestry [17,18]. Simulation studies by [19] indicates that such growth functions are so flexible to wrongly fit to given data set and recommends more care while selecting the models.
r
t
A number of attempts have been made to generalize
the growth models. For example, [17] modified the ODE (1) by including one parameter as:
d d
y
k y
t
from which some growth models
are derived. Moreover, they have shown that the model has upper limit but no inflection point when 1
1 ; and has both upper limit and inflection point for .
[18] defined 9-parameters model as:
. The first two terms include all commonly known growth functions except Weibull, and so they included to the third term to account for it.
3 3 1 1 2 2
1 2 e 3
p q y
p q p q t
y K y t K y K y e
The generalized logistic function has been studied by some researchers [6,9-11]. Eberhardt and Breiwick [9] applied the models to growth of birds and mammals populations.
In the current paper, we provide a new single general-ized growth model as solution of the ODE (1) consisting of eight parameters. It can also serve for model selection purposes. We also study the mathematical relationships among the models presented herein. Inflection points of the models are discussed.
2. Koya-Goshu Growth Function as a
Generalization of Growth Functions
In this section we define a new generalized growth func-
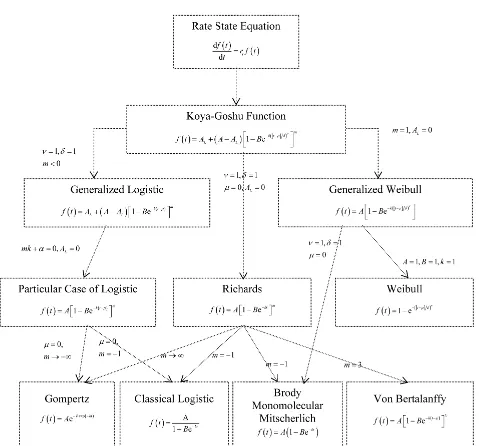
tion, named as Koya-Goshu growth function and show how it accommodates the commonly known growth models such as: Logistic, Generalized Logistic, Gom- pertz, Brody, Monomolecular, Mitscherlich, Von Berta-lanffy, Richards, Generalized Weibull and Weibull func-tions.
The new generalized growth function, Koya-Goshu growth function, is defined as
1 e m k tL L
f t A AA B (2)
Here the parameters are defined as follows: 1
1
m L
L
A A
B
A A
is derived from
A A A m, L, ,
: limt
A f t f, A is upper asymptote of f t
L
A : Lower asymptote of f t
A f
:
Growth rate parameter
Time shift, a constant :
Time scale, a constant , :m
Shape parameters of the growth function, 0, 0
m
2.1. Description of Koya-Goshu Growth Model
The Koya-Goshu growth model is 8-parameter
A A A k, L, , , , , , m
0.
function. The model is a more general solution of the ODE (1). Note that 0 and
equal at time
A A
0
B m
Regarding the quantity ,
as ;
B 1
B
B as ;
as . The quantity can assume any value in the open interval
0 B
m
0
m
,1
B1
B
0 B 1
for Richards, and in (0, 1) for both Von Bertalanffy and Brody. For both Logistic and Gompertz, can take any positive real number. For Weibull, while for generalized Weibull case,
.
When time is non-negative, the Koya-Goshu func-tion is well defined for modeling growths. The funcfunc-tion represents sigmoid curve for m < 0 and
t
any positive odd integer. However, if m > 0 or (m < 0 and is any real number other than positive odd integer), the function is well defined growth model for time ttL where
1 1log
L
t
k B
. This implies that the function misses lower asymptote in some cases. To account for the asymptote, modification can be made by taking
Lf t A for t tL or can be written as:
1 e ,
,
m t k
L L L
L L
A A A B t t
f t
A t t
Thus, the Koya-Goshu function in (2) can be generally expressed as:
1 e mk t
L L L
f t A U t t A A B
(3) Here * is used to denote multiplication. Also here
0,1,
L L
L
t t
U t t
t t
is a unit step function, where
L
t if m0 & odd positive integer or
1 1log
L
t B
k
if
m0 or
m0 & non positive odd
L
t is a lower bound for the time. Note that AL f t
Lwith f
defined by the limit of f t
as time tgoes to . It serves as a lower asymptote of f t
.Note that the Koya-Goshu function is defined at all points
m,
in m-plane. All the commonly known growth curves lay along the line 1 or m1 only. The function extends the inclusion of other points in the plane than these points. This means that it is so flexible that one can select any other curves than the commonly used ones.We show that the Koya-Goshu model accommodates all commonly known growth functions. We have given detailed analysis of the growth models and how they are related to each other. The Richards function is a general form of Brody, Von Bertalanffy, Classical Logistic and Gompertz. Brody is same as Monomolecular and Mits- cherlich functions. Brody is a special case of Weibull function. All the relations are illustrated by flow chart in Figure 1. Detailed derivations of the function f t
andrelative growth rate t are given in Appendix A. Some selected plots are illustrated in Figures 2-5.
r
2.2. Properties of the Koya-Goshu Function
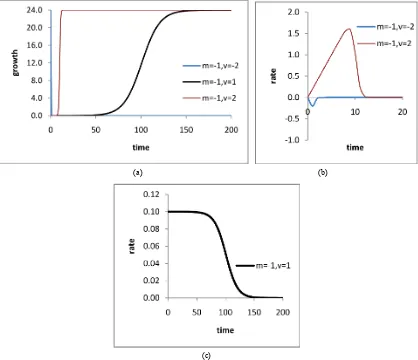
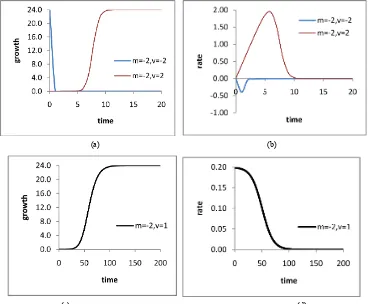
The function represents both increasing and decaying growths (see Figure 2(a), 3(a), 4(a), 5(a)). It is increas-ing for 0 and decaying for 0. This means that increasing or decaying of the growth is influenced by sign (positive or negative) of , irrespective of the val-ues of m.
The function represents increasing growths with upper asymptote but no lower asymptote:
1) For all positive combination values of both m and
(see Figures 2(a), 3(a))
2) For all small negative values of and large posi-tive values of
m
(see Figure 4(a)).
The function represents increasing growths with both upper and lower asymptotes:
Figure 1. Flow chart illustrating the relationships among the generalized and specialized growth functions.
(a) (b)
[image:3.595.102.493.550.715.2](a) (b)
Figure 3. Plots of (a) growth functions and (b) rate functions with m2,
2 1, ,2 .
(a) (b)
[image:4.595.91.509.296.656.2](c)
Figure 4. Plots of (a) growth functions and (b) (c) rate functions with m 1,
2 1, ,2 .
positive values of (see Figure 5(a))2) For all small negative values of and small posi-tive values of
m
(see Figure 4(a)).
The occurrence of either lower and upper asymptotes
or only upper asymptotes is influenced by only but not
m
. Generally, the parameter influences growth behavior, while the parameter influences asymptotic behavior of the function.
(a) (b)
[image:5.595.114.483.86.390.2](c) (d)
Figure 5. Plots of (a) (b) growth functions and (c) (d) rate functions with m 2,
2 1, ,2 .
2.3. Inflection Point of Koya-Goshu Function
We now introduce the definition of inflection points of a curve, and describe the procedure to find inflection points for the growth functions we discuss in this paper. Suppose that the function f t
is continuous on anopen interval containing the point . Then the point is called an inflection point of
' 'a
' 'a f t
provided thaton one side of and on the
other side. At the inflexion point itself either or
0
0f t
f t
' 'a
0 'f t
'a
f t does not exist [20].
1 1
1 1
1
m L
m m
L L
mk
f t f t A
t
A A f t A
(4)
1
1 1
1
1 1
L
m L
L
A A
t
f t m m
f t A
t
k f t
(5)
Here, we observe that
1
1 0
1 1
1
1 0
1 1
1 0
1 e
m L
L
L
t k
f t
A A
m
f t A
t k
m t
m k
B
(6)
Clearly, point of inflection exists in Koya-Goshu func-tion provided the relafunc-tion (5) is satisfied, since
0f t at that point and also f
t 0 and
0f t are satisfied on the increasing and decreasing
sides of that point.
Here it can be observed that the inflection points of Koya-Goshu function, when the parameters are fixed as 1)
1, 1
For the other cases when m1,1, the inflection point for the Koya-Goshu function can be obtained by approximations. For example, using Taylor series expan-sion up to first order term, the time of inflection is ap-proximated as:
1 1 2 1 2 1 11 1 4 1 1
B t
m Bk
mB mB B m
(7)
3. Biological Growth Models and the
Parametric Relationships
In this section we studied the parametric relationships among all the biological growth models considered in this paper viz., Koya-Goshu biological growth model, Generalized Logistic, Particular case of Generalized Lo-gistic, Richards, Von Bertalanffy, Brody, LoLo-gistic, Gompertz, Generalized Weibull, Weibull Monomolecu-lar, and Mitscherlich functions. The relationships identi-fied have been exhibited through a flowchart.
3.1. Generalized Logistic Function
The Generalized Logistic function as given in [21] is expressed in its original notations as
1
1 e t M
Y t
Q
which we now re-express
it with same notations used in this paper as
1 e mk t
L L
f t A AA B (8)
by replacing in the equation Y t
f t
,AL,, ,
A k M
1
m and
1
– 1 L m
L A A Q A A .
The Generalized Logistic function (7) is hereby a spe-cial case of Koya-Goshu function with 1, 1, and
. The parameter B takes the form 0
m
1
1 L m
L A A B A A
. The expression for the relative
growth rate function can be computed as
1 1 ( ) m L L t Lf t A
A A
r mk
f t A f t
. Similarly, the
expressions for f
t and f
t are, respectively,given by
1 1
1
1m m m
L L
f t mk f t A AA f t AL
and
1
1
1 L m 1
L
A A
f t mk f t
m f t A
.
The single point of inflection occurs when the organism
reaches the growth
1 1m
L L
f t A A A
m
at
time
1
1
log 1 L m
L
A A
t m
k A A
where m
0,1 . For 0 , inflexion point does not exist.1
m
3.2. Particular Case of the Generalized Logistic Function
A function called Particular case of the Generalized Lo-gistic function is defined [21] as
0 1
1 e t t
Y t
Q
which we now re-express it
with same notations used in this paper as
1 e mk t
f t A B (9)
by replacing in the equation
01
, , , ,
Y t f t A k t
m
and
1 –Q 1 A m
A
. Note that Equation (8) is a special
case of Equation (7) for Generalized Logistic function with AL0,mk 0 In this case, the parameter B
takes the form as
1
1 A m
B
A
. The expression for the
relative growth rate function can be computed as rt
1 1 m L tf t A
A
r mk
f t f t
. Similarly, the ex-
pressions for f
t and f
t are respectively givenby
1 1
1 1
m m m
f t mkf t A f t
and
1
1
1 A m 1
f t mk f t
m f t
point of inflection occurs when the organism reaches the
growth
1 1m
f t A
m
at time
1
1
log 1 ,
0,1
m
A
t m
k A
m
1
For 0m , inflexion point does not exist.
3.3. Richards Function
The Richards function is defined as in the usual notations (Richards, 1959) as
1 ekt mf t A B (10)
Here
1 0
1 A m
B
A
. The Richards function can be directly derived from the ODE or rate-state Equation (1)
with relative rate function
11
m
t
A
r mk
f t
. The
Richards function becomes special case of Koya-Goshu growth model with 1, 1, 0,AL 0. Here the parameter m can assume any non-zero real number. The expressions for f
t and f
t
are given by respec-tively
1 m
m m
1 1 1
f t mkf t A f t
and
m1
1
m1
1m
f t kf t f t m A m f t
The
sin-gle point of inflection occurs when the growth reaches 1 m
m m
of its final growth, i.e.
1m
m f t
m
A
at time
1 0
1 log 1 A m , 1.
t m m
k A
3.4. Von Bertalanffy FunctionVon Bertalanffy is defined (Bertalanffy, 1957) as
31 ekt
f t A B (11)
It is a special case of Richards function (5) with and a special case of Koya-Goshu growth model with
3
m
1, 1, 0,AL 0,m 3
. Here
1 3 0
1 A
B
A
. It can also be derived from ODE (1) with
relative rate function
1 3 3t
A
r k
f t
1
. For Von
Bertalanffy function f
t and f
t are respectivelygiven by
2 1 1
3 3 3
3
t kf t A f t
f
and
3 2 13
13 13
2 13 3 13
f t k f t A f t A f t
. Here
the single point of inflection occurs when the growth reaches
8 27
of its final growth, i.e.
t 8 27
A at time1 3 0 1
log 3 1 A
t
k A
.
f
3.5. Brody Function
Brody is defined (Brody, 1945) as:
1 e kt
f t A B (12)
It is a special case of Richards function (9) with 1
m and a special case of Koya-Goshu growth model
with. 1, 1, 0, 0, 1, 1 0
L
A
A m B
A
. It can
also be derived from ODE (1) with rate function
1t
A
r k
f t
. Here f
t and f
t are respec-tively given byf
t k A f t
and
2
f t k A f t . Brody growth function does not
possess a point of inflexion since f
t 0 is not sat-isfied for any value of . t3.6. Logistic Function
The classical Logistic function (Nelder, 1961) is defined as:
A1 e kt
f t
B
(13)
Here
0
1
A B
A
. The Logistic function is a spe-
cial case of
1) Richards function (9) with m 1
2) Particular case of logistic function (8) with 0,m 1
3) Generalized logistic function (7) with 0,AL 0,m 1, k
4) Koya-Goshu function (2) with 1, 1, 0,AL 0,m 1
.
tA f t
r k
A
. Here, f
t and f
t arerespec-tively given by f
t k f t
1 f t
A
and
1 2f t
f t kf t
A
. The single point of inflection
occurs when the growth reaches half of its final growth
2
A
f t at time
0 1 log
1
A k A t .
3.7. Gompertz Function
The Gompertz function (Winsor, 1932) is defined as
exp e B kt
f t A (14)
where 0 log A B A .
It is shown to be a special case of 1) Richards function (9) with 2) Particular case of logistic function (8) with 3) Generalized logistic function (7) with
m
m
0,AL 0,m
,
0, L
4) Koya-Goshu function (2) with 1, 1, A 0,m . The
Gompertz function can be derived from the ODE (1) with
rate function
log t A r k f t . Here,
log
A
f t k f t
f t
,
log A
1f t kf t
f t
and the single point of
inflection occurs when the growth reaches
1 e of its final growth, i.e., f t
1 e A at time0 1
log log A t k A .
3.8. Generalized Weibull Function
The Weibull function is generalized and named here by Generalized Weibull function as
1 et K
f t A B
(15)
where B 1 A
A
. The generalized Weibull is a special
case of Koya-Goshu growth function (2) with . Generalized Weibull functions can be
derived from the ODE (1) with rate function
1, L 0
m A
11
t
k t A
r f t
. For Generalized Weibull,
f t and f
t are respectively given by
tf t k A f t
and
11 t 1 t
t k f t
f
. The
single point of inflection occurs when the organism
reaches the growth
1 1
1 e
f t A B
at time 1 1 t k .
3.9. Weibull Function
The Weibull growth model (Rawlings et al., 1998) is given as
1 e t f t (16)
The Weibull function can be derived from the ODE (1)
with rate function
1
1 t
k t A
r f t .
Weibull a special case of Generalized Weibull (13) func- tion with A1,B1,k1 and that of Koya-Goshu growth function (2) with
1, L 0, 1, 1, 1
m A A B k . For Weibull, f
t and
f t are respectively given
byf
t 1 f t
t
and
1 t 1
1
t
f t f
t
. For
Weibull, the single point of inflection occurs when the
organism reaches the growth
1 1
1 e
f t
at time 1 1
t
. This fact can be verified by
directly substituting A1,B1,k1 in the inflection point of Generalized Weibull.
3.10. Monomolecular and Mitscherlich Functions
Mitscher-lich growth functions are the same, except that the names and notations used are different. Hence, all these three functions exhibit the same properties and behaviors and also they represent the same growth patterns.
Monomolecular growth function is defined (France et al., 1996), in its original notations, as
00 e 1 1 e
t t
f f f
f
w
w t w w w w
w
where w t
is the growth function at time , t wf is the final (mature) value, 0 at is the initial value andww t0
is rate of growth. This function can be expressed as Brody function (7) with notations
00 0
, f , , 1 w ,
w f t w A w A B k
w
asf t
A
1Bekt
. Monomolecular growth function can be derived from the ODE (1) with rate function
1
t f
r w w or
1t A r k f t .
Thus, Monomolecular growth function, just similar to Brody growth function, does not possess a point of in-flexion since f
t 0 is not satisfied for any value of. t
Mitscherlich growth function [22] is defined, in its original notations, as 1 e t
y where is y
the growth function at time , t is the final (mature) growth, is a constant and is rate of growth. The Mitscherlich function can be expressed with notations
, , , e ky f t A k B
as Brody function
1 e kt
f t A B given by (7). It can be derived from
the ODE (1) with rate function
t y r y
or t
1A r k f t .
Not that the integral constant becomes
log AB log . Thus, Mitscherlich growth function, just similar to Brody growth function, does not possess a point of inflexion since f
t 0 is not sat-isfied for any value of . t4. Other Relationships
Here we derive explicitly and present few more relation-ships, other than those mentioned in Section 3, among the growth models considered in this paper.
4.1. Relation between Richards and Logistic Functions
Let us now see how Richards and Logistic functions are related. Using the Richards function (9), we can derive Logistic (12) as follows:
1 0
Richards 1 e
1 1 e
m kt
m m
kt
f t A B
A A A (17)
1 1 0 1 0 0Richards with 1
1 1 e
1 1 e
1 e
1 1 e
kt
kt
kt kt
f t m
A A A A A A A A B A A (18) where 1 0
1 A m
B
A
. Hence, Richards growth function with
m 1
leads to the Logistic function.4.2. Relation between Richards and Gompertz Functions
We now show how Gompertz is related to Richards function, i.e., the relative growth rate function of Rich-ards as leads to that of Gompertz, which is now shown. Note that the relative growth rate functions of Gompertz and Richards are given respectively by
m
log t A r k f t and
1 1 m t A r mk f t .
By applying the limit as on Richards , we get the following:
m rt
1 lim Richards lim 1 1exp log 1
lim 1 m t m m m r A mk f t A
m f t
k m (19)
Here the last expression is obtained by a simple alge-braic rearrangement of the expression. In this expression
evaluation of limit leads to 0 0
applying L-Hospital rule to get
2 2 lim Richards 1 1exp log log
lim
1
1
lim exp log log
log Gompertz m t m m t r A A
m f t m f t
k
m
A A
k
m f t f t
A k r f t (20) Thus, the limiting value of the Richards relative rate growth function as reduces to the Gompertz relative rate growth function, and hence these two func-tions are related.
m
4.3. Relation between Particular Case of Generalized Logistic and Gompertz
We now show how Gompertz is related to the particular case of generalized Logistic function, i.e., the relative growth rate function of the particular case of generalized Logistic as leads to that of Gompertz, which is now shown. Note that the relative growth rate func-tions of Gompertz and the particular case of generalized
m
Logistic are given respectively by
log t A r k f t , and
11 where 0 m
t
A
r mk m
f t .
By applying the limit as on rt of the
par-ticular case of generalized Logistic function, we get the following:
m
1 lim lim 1 1exp log 1
lim 1 m t m m m
r par case gen Log
A mk
f t
A
m f t
k m (21)
Here the last expression is obtained by a simple alge-braic rearrangement after the inverse functions viz, loga-rithmic and exponential operations are used. In this ex-
pression evaluation of limit leads to 0 0
and to avoid
that we apply L-Hospital rule to get
2 2 lim 1 1exp log log
lim
1
1
lim exp log log
log Gompertz
m t
m
m
t
r par case gen Log
A A
m f t m f t
k
m
A A
k
m f t f t
A k r f t (22) Thus, the relative rate growth function the particular case of generalized logistic function as re-duces to the Gompertz relative rate growth function, and hence these two functions are related.
m
4.4. Relation between Brody and Gompertz Functions
We have shown in the flow chart the relationships among the growth functions by setting the parameters suitably. However, Gompertz and Brody functions can be related through a transformation of time coordinate and that goes as follows:
Let the time variables of Brody and Gompertz are rep-resented by and t respectively. Now consider the Brody function as
1 e kt 1 1 A0 e ktf t A B A
A
(23)
and the Gompertz function as
0 0 0 0 exp expexp log exp
exp log exp
exp exp exp exp
f A B k
A A A k
A A A k
A A A k
A k (24)
Now on equating the f t
and f
from (23)and (24), we get
0
0
1 1 A e kt exp exp
A A
A k
(25)
and this can be expressed as
0
0 1 log exp exp A A t
k A A k
[image:11.595.83.529.111.737.2]
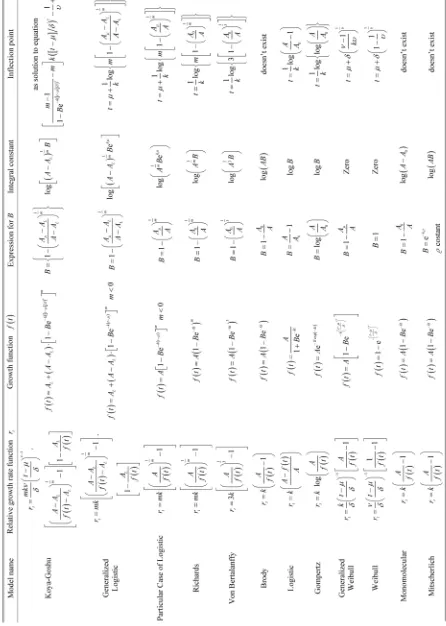
Table 1. List of
growth functions and thei
r r
es
p
ective
rat
e fu
n
ction
s,
exp
res
si
on
s for b
,
in
teg
ral
con
stan
ts
and
in
flect
ion
p
o
which is the coordinate transformation equation between the time variables of Brody and Gompertz functions.
5. Illustration for How Relative Growth Rate
Function Behaves—Richards Case
The relative growth rate function t is significantly
dif-ferent for the models at early ages and converges to zero for the later ages. The relative growth rate t is an
in-creasing function of while it is a decreasing with time t. However, t grows with in the early ages
allowing the parameter m to play a significant role. Sub-sequently, t dies at later ages irrespective of . We
consider Richards function as example to illustrate this. r
m
r m
r
r m
Consider the Richards relative growth rate function :
t
r
1
1 m
t
A
r mk
f t
(27)
is a function of parameter and time , and limit gives:
m z
1 1
0 0
0
limt rt mklimt A m 1 mk A m 1
f t A
(28) Equation (28) t is increases with m at early times. Also, on taking the limit of in (27) as t , we get
r
t
r
1
limt rt mklimt A m 1 0
f t
showing that vanishes at time of growth maturity for
all . t
r m
6. Conclusion
This paper introduces a new generalized mathematical model for biological and other growths, named as Koya- Goshu growth model. It is a generalization of the com- monly used growth functions such as: Brody, Von Ber- talanffy, Richards, Weibull, Monomolecular, Mitscher- lich, Gompertz, Logistic and generalized Logistic func- tions. Koya-Goshu model is constructed as a solution of ordinary differential or rate-state equation. The function incorporates two parameters where one influences grow- th pattern and the other influences asymptotic behavior. The model is so flexible that it can be useful in model selections. Moreover, it generates new and useful growth functions. All of the growth models considered under the study are related to each other as illustrated in the flaw
chart. As further studies, we will take up applications of this model for data fitting and prediction.
REFERENCES
[1] S. Brody, “Bioenergetics and Growth,” Reinhold Pub- lishing Corporation, New York, 1945.
[2] L. von Bertalanffy, “Quantitative Laws in Metabolism and Growth,” The Quarterly Review of Biology, Vol. 3,
No. 2, 1957, p. 218.
[3] F. J. Richards, “A Flexible Growth Function for Empiri- cal Use,” Journal of Experimental Botany, Vol. 10, 1959,
pp. 290-300.http://dx.doi.org/10.1093/jxb/10.2.290 [4] J. France and J. H. M. Thornley, “Mathematical Models
in Agriculture,” Butterworths, London, 1984, p. 335. [5] C. P. Winsor, “The Gompertz Curve as a Growth Curve,”
Proceedings of National Academy of Science, Vol. 18, No.
1, 1932, pp. 1-8.http://dx.doi.org/10.1073/pnas.18.1.1 [6] J. A. Nelder, “The Fitting of a Generalization of the Lo-
gistic Curve,” Biometrics, Vol. 17, No.7, 1961, pp. 89- 110.http://dx.doi.org/10.2307/2527498
[7] J. E. Brown, H. A. Fitzhugh Jr. and T. C. Cartwright, “A Comparison of Nonlinear Models for Describing Weight- Age Relationship in Cattle,” Journal of Animal Science, Vol. 42, No. 4, 1976, pp. 810-818.
[8] T. B. Robertson, “On the Normal Rate of Growth of an Individual and Its Biochemical Significance,” Archiv für
Entwicklungsmechanik der Organismen, Vol. 25, No. 4,
1906, pp. 581-614.
http://dx.doi.org/10.1007/BF02163864
[9] L. L. Eberhardt and J. M. Breiwick, “Models for Popula-tion Growth Curves,” ISRN Ecology, Vol. 2012, 2012,
Article ID: 815016.
http://dx.doi.org/10.5402/2012/815016
[10] D. Fekedulegn, M. P. Mac Siurtain and J. J. Colbert, “Pa- rameter Estimation of Nonlinear Growth Models in For- estry,” Silva Fennica, Vol. 33 No. 4, 1999, pp. 327-336.
[11] F. J. Ayala, M. E. Gilpin and J. G. Ehrenfeld, “Competi- tion between Species: Theoretical Models and Experi- mental Tests,” Theoretical Population Biology, Vol. 4,
No. 3, 1973, pp. 331-356.
http://dx.doi.org/10.1016/0040-5809(73)90014-2
[12] J. O. Rawlings and W. W. Cure, “The Weibull Function as a Dose Response Model for Air Pollution Effects on Crop Yields,” Crop Science, Vol. 25, 1985, pp. 807-814.
http://dx.doi.org/10.2135/cropsci1985.0011183X0025000 50020x
[13] J. O. Rawlings, S. G. Pantula and D. A. Dickey, “Applied Regression Analysis: A Research Tool,” Springer, New York, 1998.
[14] W. J. Spillman and E. Lang, “The Law of Diminishing Increment,” World, Yonkers, 1924.
[15] J. France, J. Dijkstra and M. S. MDhanoa, “Growth Func-tions and Their Application in Animal Science,” Annales
De Zootechnie, Vol. 45, Suppl. 1, 1996, pp. 165-174.
http://dx.doi.org/10.1051/animres:19960637
Parameters of Linear and Nonlinear Growth Curve Mod- els at Early Growth Stage in California Turkeys,” Archiv
für Geflügelkunde, Vol. 71, No. 4, 2007, pp.175-180.
[17] Y. C. Lei and S. Y. Zhang, “Features and Partial Deriva-tives of Bertalanffy-Richards Growth Model in Forestry,”
Nonlinear Analysis: Modelling and Control, Vol. 9, No. 1,
2004, pp. 65-73.
[18] B. Zeide, “Analysis of Growth Equations,” Forest Sci-ence, Vol. 39, No. 3, 1993, pp. 594-616.
[19] A. T. Goshu, “Simulation Study of the Commonly Used Mathematical Growth Models,” Journal of the Ethiopian
Statistical Association, Vol. 17, 2008, pp. 44-53.
[20] C. H. Edwards Jr. and D. E. Penney, “Calculus with Ana-lytic Geometry,” Printice Hall International, New Jersey, 1994.
[21] Generalised logistic function
http://en.wikipedia.org/w/index.php?oldid=472125857 [22] R. A. Mombiela and L. A. Nelson, “Relationships among
Some Biological and Empirical Fertilizer Response Mod-els and Use of the Power Family of Transformations to Identify an Appropriate Model,” Agronomy Journal, Vol.
73, No. 2, 1981 pp. 353-356.