Interest Rate Rigidity and the Fisher Equation
Full text
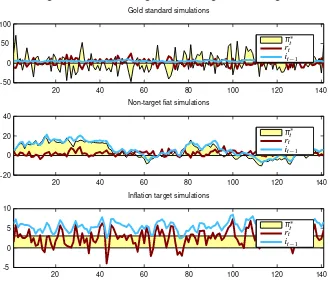
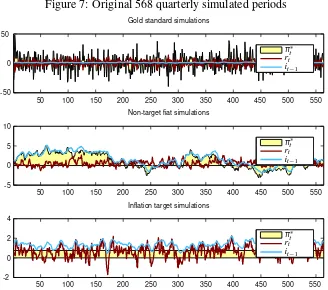
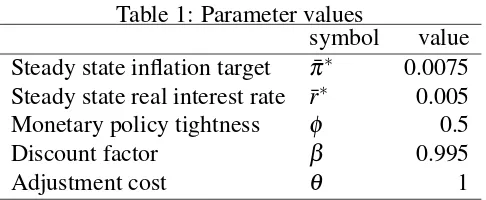
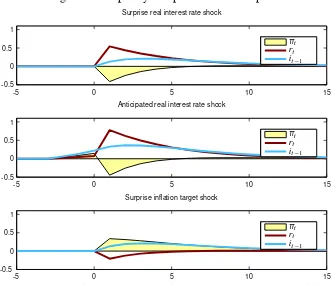
Figure


Related documents
Lagged value of nominal interest rate, growth in future real income and money supply has positive and significant effect on nominal interest rates. Real income growth, lagged
Results on the long-run properties of nominal interest rates, inflation rates, and real interest rates ADF tests allowing for a structural break in the mean reject a unit root in
In region IVa, asset prices and real interest rates are negatively correlated (nominal interest rates are constant at zero, but an increase in inflation makes real assets
Thus, this section starts by introducing the different models used to estimate expected inflation and inflation volatility, followed by presenting the Fisher
Since the central bank strictly targets inflation in the traded sector and nominal exchange rates are fixed, the real exchange rate depreciation translates into a fall in the
This paper explores the hypothesis that high volatility of real and nominal exchange rates may be due to the fact that local currency pricing eliminates the pass-through from changes
Engel and Zhu (2017) suggest that, under a rigidly fixed nominal exchange rate regime, the excess volatility puzzle of real exchange rates practically disappears or becomes minor
As the nominal exchange rate is fixed, this inflation leads to a real exchange rate depreciation that makes the real marginal costs even higher, but in the