Intensity–duration–frequency (IDF) rainfall curves in Senegal
Full text
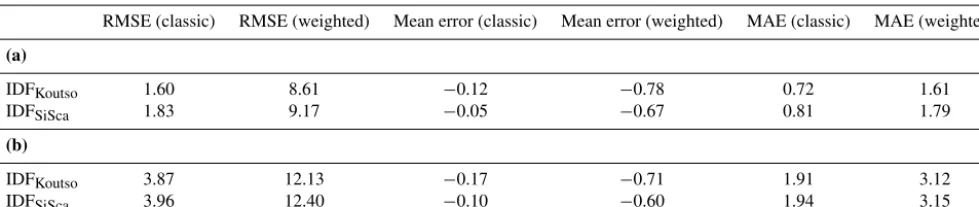
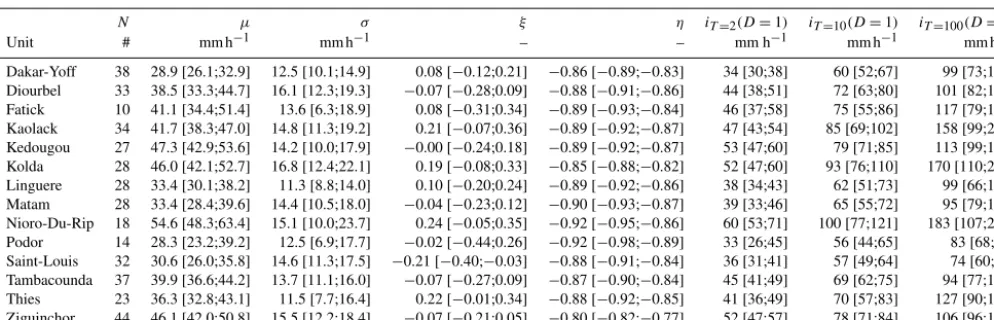
Figure


![Figure 6. Comparison between IDFTSiSca and IDFKoutso in calibration mode. Top panels: location parameter – µ(D) [mmh−1]; scale pa-rameter – σ(D) [mmh−1]; and shape parameter – ξ [–]](https://thumb-us.123doks.com/thumbv2/123dok_us/8325075.1380279/7.612.112.485.65.366/figure-comparison-idftsisca-idfkoutso-calibration-location-parameter-parameter.webp)
Related documents
In particular, a Stage 3 Emergency must be declared, and firm load shedding must commence, when conditions threaten the CAISO’s ability to maintain the CAISO’s Spinning
In order for teachers to develop ownership of professional development, they need to be active participants in its construction, tailoring programs to their needs and
A strong blue dye appeared by iron staining and showed a high accumulation of con- jugated nanoparticles on the membrane of PC3 cells by oriented conjugation via
We thus see a confluence of three density-related factors that in combination help to explain the severity of congestion in Los Angeles: (1) congestion is likely to rise with
Slauson Ave Build dual managed grade separation at Western Ave Lakewood Blvd Convert parking lanes to travel lanes from Carson St to Del Amo Blvd (1.6 miles, 3.2 converted
Page 19…Figure 7: Federal, State, and Local Shares of Taxes Collected from Immigrant Households in the Washington DC, Metropolitan Area, circa 1999-2000 Page 20…Figure 8: Share
The purpose of this docket is to renew the approval of an existing export of up to 35.65 million gallons per month (mgm) (1.15 million gallons per day (mgd)) of water from the
Lord Tugendhat Viscount Ullswater Lord Vaizey of Didcot Baroness Vere of Norbiton Baroness Verma Lord Vinson Lord Wakeham Lord Wasserman Lord Wei Lord Wharton of Yarm Lord


![Figure 10. Maps of IDF[mmhSiSca parameters: µ0 [mmh−1], σ0−1], ξ [–], and η [–].](https://thumb-us.123doks.com/thumbv2/123dok_us/8325075.1380279/10.612.67.266.64.549/figure-maps-of-idf-mmhsisca-parameters-mmh-and.webp)