Chapter 1
ELECTROSTATICS I
ELECTRIC FIELD AND SCALAR
POTENTIAL
1.1
Introduction
Atoms and molecules under normal circumstances contain equal number of protons and electrons to maintain macroscopic charge neutrality. However, charge neutrality can be disturbed rather easily as we often experience in daily life. "Static electricity" induced when walking on a carpet and caressing a cat is a familiar phenomenon, and is known as frictional (or tribo) electricity. Before the invention of chemical batteries (Volta, 1786), electricity generation had been largely done by frictional electricity generators. In nature, lightnings are caused by electrical discharges of electric charges accumulated through friction among cloud particles. In frictional electricity, mechanical disturbance given to otherwise charge neutral molecules either splits electrons o¤ a material body, or adds them. For example, if an ebony rod is rubbed with a piece of fur, electrons are transfered from the fur to the ebony, and the ebony rod becomes negatively charged, while the fur becomes positively charged.
Charge neutrality can be disturbed by various other means, such as thermal, chemical, optical and electromagnetic disturbances. It is well known that even a candle ‡ame is weakly ionized (cuased by thermal ionization) and responds to an electric …eld. Chemical batteries are capable, through chemical reactions, of separating charges. Some metals are known to emit electrons when exposed to ultraviolet light (photoelectric e¤ect discovered by Hertz in 1897 and later given quantum mechanical explanation by Einstein). Finally, as an example of electromagnetic means of charge separation, the plasma (ionized gas) state in ‡uorescent lamps and plasma TV may be added to the list.
Charged bodies exert electric forces (Coulomb force) on each other. Systematic experiments on electric forces had been carried out by Cavendish and Coulomb in the 18th century and led
to the establishment of the Coulomb’s law. Like charges repel each other, while unlike charges attract each other. Therefore, in any attempt to separate charges out of an initially charge neutral body, energy must be added. For example, in frictional electricity, mechanical energy is expended to separate charges. In chemical batteries, chemical energy is converted into electric energy, and in electric generators, either gravitational (as in hydropower generation) or thermal (as in steam power plants) energy is converted into electric energy.
The Coulomb force to act between two charges is inversely proportional to r2 where r is the separation distance between the charges. A hydrogen atom consists of one electron ”revolving” around a proton. The centripetal Coulomb force (attracting) is counterbalanced by the mechanical centrifugal force, and the electron stays on a circular orbit. (This is a classical electrodynamic model. For a more satisfactory description of a hydrogen atom, quantum mechanical analysis is required. However, the concept of force balance is basically correct.) A nucleus of heavier atoms contains more than one proton. The size of a nucleus is of order 10 15 m (compare this with the atomic size 10 10 m). Therefore, among the protons packed in a nucleus, a tremendously large repelling Coulomb force should act, and some other force, which is not of electric nature, must keep protons together. This is provided by the so-called ”strong” nuclear force which acts among hadrons such as protons and neutrons. Obviously, the nature of nuclear force is beyond the realm of classical electrodynamics. However, it should be realized that nuclear energy that can be released when a heavy nucleus (such as U235) splits (nuclear …ssion process) is nothing but electric energy stored in a nucleus.
Electrostatics is one branch of electrodynamics in which electric charges are either stationary or moving su¢ ciently slowly so that magnetic …eld induction and electromagnetic radiation can be ignored entirely. All basic laws in electrostatics (Gauss’law, Maxwell’s equations) follow from the Coulomb’s law. Therefore, formulating the electric …eld and scalar potential in electrostatics will be deduced from this fundamental law. It should be pointed out that electrostatics (together with mag-netostatics) provides us with preparation for more general electrodynamics, electromagnetic wave phenomena in particular. For example, electromagnetic wave propagation in a medium (including vacuum) requires that the medium be able to store both electric and magnetic energy. Obviously, electric energy storage leads us to the concept of capacitance. Calculation of the capacitance of a given electrode system is one important application of electrostatics, but the concept of capacitance (and inductance) will also play fundamental roles in dynamic electromagnetic phenomena.
1.2
Coulomb’s Law
In the late 1700’s, Cavendish and, independently, Coulomb carried out extensive research on static electricity. (At that time, no batteries were available, and electricity generation was mainly done with frictional electricity machines.) Apparently, Cavendish’s discovery of the inverse square law, now known as Coulomb’s law, was made before Coulomb. However, Cavendish did not publish his large amount of work on electricity, while Coulomb wrote several papers on electricity and magnetism. Of course, Cavendish is best known for his gravitational torsion balance experiments
which experimentally veri…ed the inverse square law of gravitational force originally postulated by Newton. Both Cavendish and Coulomb used similar torsion balance apparatus to measure electric forces acting between charged bodies.
Coulomb’s law is stated as follows. When two charges q1 and q2 are at a distance r from each
other, the electric force exerted on each other is proportional to q1q2
r2 ,
F =const.q1q2
r2 : (1.1)
In the MKS-Ampere unit system (SI unit system), the charge is measured in Coulombs (C), the distance in meters (m), and the force in Newtons (N). In these units, the constant experimentally determined is
constant = 8:99 109 N m
2
C2
Figure 1-1: Repelling Coulomb force between like charges.
The force is a vector quantity. In the case of the Coulomb force, the force is directed along the separation distance vector r,and a more formal expression is given by
F=const.q1q2
r2 er (1.2)
where
er= r
r (1.3)
is the unit vector along the position vector r. Of course, both charges q1 and q2 experience a
force of the same magnitude, but oppositely directed. The sign of the product q1q2 can be either
positive or negative. When q1q2 > 0, the force is repelling, and when q1q2 < 0, the force is
of two kinds of charges, positive and negative, was known although their origin, namely charged elementary particles, was clari…ed much later. The electron was discovered by Thomson in 1897. The electronic charge presently established is 1:6 10 19 Coulomb.
The proportional constant in the Coulomb’s law corresponds to the force to act between two equal charges, 1 C each, separated by a distance of 1 m. By arranging such an experimental situation, the constant could be measured as done by Cavendish and Coulomb. (In more modern methods, the velocity of light in vacuum provides an indirect measurement of the constant. This will become clear later in Chapter 7.) In the MKS-Ampere unit system, the connection between mechanical force (Newtons) and basic electromagnetic unit is actually made in terms of magnetic force, rather than the Coulomb force, as will be explained in Chapter 7. When two long parallel currents of equal magnitude separated 1 m exert a force per unit length of 2 10 7 N/m, the magnitude of the current is de…ned to be 1 Ampere. The electric charge, 1 C, is then deduced from,
1C= 1Ampere 1sec
In other unit systems, the Coulomb’s law itself is employed to de…ne the unit of electric charges. For example, in the CGS-ESU (ESU for ElectroStatic Unit) system, when two equal charges separated by 1 cm exert a force of 1 dyne on each other, the charge is de…ned to be 1 ESU. Since 1 N = 107
dyne, and 1 m = 102 cm, we can readily see that
1 C = p 1 ESU
8:99 1018 '
1 ESU
3:0 109
For example, the electronic charge in ESU is
1:6 10 19 3:0 109= 4:8 10 10 ESU
Although in engineering, the MKS-Ampere (SI) unit system is universally accepted, the CGS-ESU and associated Gaussian unit system is still popular in physics. Both have merits and demerits, and it is di¢ cult to judge one unit system superior to the other.
In the MKS-Ampere unit system, the Coulomb’s law
F= 8:98 109q1q2
r2 er (N) (1.4)
is rewritten as
F= 1 4 0
q1q2
r2 er (N) (1.5)
where
0 = 8:85 10 12
C2
N m2 (1.6)
is called the vacuum permittivity. The appearance of the numerical factor4 may be uncomfortable, but cannot be entirely avoided. If we do not introduce the factor 4 in the Coulomb’s law, it will pop up in the corresponding Maxwell’s equation. In fact, the Maxwell’s equation for the static
Figure 1-2: In MKS unit system,I =1 Ampere current is de…ned if the force per unit length between in…nite parallel currents 1 m apart is 2 10 7 N/m. The magnetic permeability
0 = 4 10 7
H/m is an assigned constant to de…ne 1 Ampere current.
electric …eld in the CGS-ESU system has to be written as
rE= 4 (1.7)
because the factor 4 is avoided in the corresponding Coulomb’s law,
F= q1q2
r2 er (dynes)
The newly introduced constant 0 is one of the fundamental constants in electrodynamics. Note
that 0 is a measured constant, since it is derived from the original measured constant, 8:99 109
N m2/C in the Coulomb’s law. The permittivity of air (room temperature, 1 atmospheric pressure) is about 1:0004 0 due to the polarizability of air molecules. For practical applications, the air
permittivity can be very well approximated by the vacuum permittivity.
1.3
Electric Field E
Interpretation of Coulomb’s law was a matter of debate before the concept of electric …eld was well established by Faraday and Maxwell. Before Faraday and Maxwell, the so-called “theory of action at distance” once prevailed. According to this theory, electric e¤ects (such as Coulomb force) appear through some sort of direct interaction between charges, and space (or vacuum) has nothing to do with the interaction. In the “…eld” theory, a single charge “disturbs” space surrounding it by creating an electric …eld. The Coulomb force to act between two charges is due
to interaction between one charge and the electric …eld produced by the other. The …eld theory is now well accepted, and modern electrodynamics is almost entirely described by …eld quantities such as electric and magnetic …elds.
Let us write down the Coulomb force again,
F= 1 4 0
q1q2
r2 er
This can be written either
F= 1 4 0
q1
r2er q2 (1.8)
or
F= 1 4 0
q2
r2er q1 (1.9)
We may interpret Eq. (1.8) as the force experienced by a charge q2 placed in an electric …eld,
E1=
1 4 0
q1
r2er (1.10)
produced by a chargeq1while Eq. (1.9) as the force experienced by a chargeq1 placed in an electric
…eld,
E2=
1 4 0
q2
r2er (1.11)
produced by a charge q2. A single charge q in the space with a permittivity thus produces an
electric …eld given by
E= 1 4 0
q
r2er (N/C) (1.12)
regardless of the presence of a second charge. Numerically, the electric …eld is equivalent to a force to act on a unit change. Since the force is a vector, so is the electric …eld, and complete determination of an electric …eld requires three spatial components.
In general, if a charge q is placed in an electric …eld E, the force to act on the charge is given by
F=qE (N) (1.13)
This may alternatively be used for de…nition of an electric …eld, namely, if a stationary charge q experiences a force proportional to the amount of the charge, then we de…ne that an electric …eld is present. (Elementary particles such as protons and electrons do have masses, and they experience gravitational forces as well. However, gravitational forces are orders of magnitude smaller than electromagnetic forces, and in most practical applications, gravitational forces can be ignored.) Although Eq. (1.12) has been deduced from Coulomb’s law, the inverse is not always true, that is, electric …elds are not necessarily due directly to charges. A time varying magnetic …eld produces an electric …eld (Faraday’s law). Also, an object travelling across a magnetic …eld experiences an electric …eld (motional electromotive force), as we will study in Chapter 9. However, regardless of the origin of the electric …eld, the force equation, Eq. (1.12), holds.
q
q
1
2
E
E
1 2
E
tP
Figure 1-3: Vectorial superposition of electric …eld.
1.4
Principle of Superposition and Electric Field due to a
Distrib-uted Charge
The expression for the electric …eld due to a point charge,
E= 1 4 0
q
r2er (1.14)
can be applied repeatedly to …nd an electric …eld due to a system of charges. For example, if there are two charges q1 atr1 and q2 atr2, the total …eld can be found from,
E= 1 4 0
r r1
jr r1j3
q1+
1 4 0
r r2
jr r2j3
q2 (1.15)
Note that the quantities,
r r1
jr r1j
; r r2
jr r2j
are the unit vectors in the directions r r1 and r r2, respectively. For larger number of charges,
the total electric …eld can still be found as vector sum of electric …elds due to individual charges. This is known as the principle of superposition. For N discrete charges, the electric …eld can be written down as,
E= 1 4 0
N X
i=1
r ri
jr rij3
qi (1.16)
As the number of charges increases, the summation becomes rather awkward. In most practical applications, the charge distribution can be regarded continuous, rather than discrete. As one
would expect, the summation in the case of discrete charges can be replaced by an integral in the case of a continuous charge distribution.,
A continuous charge distribution can be described by a local charge density,
(r) (C/m3)
which may vary as a function of position r. Since the size of elementary particles is so small, a collection of those particles (e.g. electrons) can be well approximated by a continuous function
(r), just as we treat water as a ‡uid although, microscopically, water consists of discrete water molecules.
Let us pick up a small volumedV0 located at a distance r0 from a reference point O as shown in Fig. 1.4. The charge contained in the volume dV0 located atr0 is
dq= (r0)dV0
By choosing the volume element su¢ ciently small, we may regard the charge dq a point charge. We already know how to express the electric …eld due to a point charge,
dE = 1 4 0
dq(r r0)
jr r0j3
= 1
4 0
r r0
jr r0j3 (r0)dV0 (1.17)
Therefore, the electric …eld at rcan be calculated from the following integral,
E(r) = Z
dE= 1 4 0
Z
r r0
jr r0j3 (r
0)dV0 (1.18)
This is a general formula for calculating an electric …eld due to an arbitrary distribution of charges. Remember that we have derived it from the Coulomb’s law.
Although the formula we just derived is a complete solution for static electric …elds due to a charge distribution, it is seldom used in practical applications except for simple (or often trivial) cases. There are several reasons for this. First, Eq. (1.18) is a vector equation. In the cartesian coordinates, for example, three components, Ex; Ey and Ez will have to be evaluated separately. That is, we have to carry out integrations three times for a complete vector solution. Second, in many potential boundary value problems, the charge distribution, (r), is not knowna priori. For example, in evaluation of a capacitance of a given electrode system, the problem is reversed, that is, we calculate the electric …eld (from the scalar potential) …rst, and then evaluate the charge distribution on the surface of electrodes. As we will study in Section 2, the method based on the scalar potential is more convenient in practical applications than evaluating the electric …eld using Eq. (1.18). However, if the charge distribution is known, we can certainly use Eq. (1.18) to evaluate the electric …eld at an arbitrary point. Let us work on some simple examples.
dq =
ρ
dV'
r'
r
r - r'
dE
O
Figure 1-4: Di¤erential charge dq= dV0 produces a di¤erential electric …elddE:
Charge Sheet
Let a large, thin insulating sheet carry a uniform surface charge density (C/m2) (= constant). If the sheet is large enough, or the point at which we wish to evaluate the electric …eld is close enough to the sheet, the electric …eld should be perpendicular to the sheet because of cancellation by an element located opposite with respect to the origin O. Choosing the cartesian coordinates
x; y; z, we then have to evaluate only the zcomponent of the electric …eld at a distance zfrom the sheet.
Let us pick up a surface element dx0dy0 located at (x0; y0; z0 = 0) on the sheet. The element carries a “point charge”dq= dx0 dy0. Then, the magnitude of the electric …eld on thez axis is,
dE= 1 4 0
dx0dy0
x02+y02+z2 (1.19)
and its z component is,
dEz= 1 4 0
z
(x02+y02+z2)3=2dx
0dy0 (1.20)
Therefore, the electric …eld on the axis is given by the following integral,
Ez= z 4 0
Z 1
1
Z 1
1
dx0dy0
(x02+y02+z2)3=2 (1.21)
However, the double surface integral can be replaced by a single integral over the radius r0, where
r02=x02+y02 so that
Ez = z 4 0
Z 1
0
2 r0 (r02+z2)3=2dr
The integral is elementary, and we …nd
Ez = z 2 0
1
p
r02+z2
r0=1
r0=0
= 2 0
z
jzj (1.23)
where pz2=jzjhas been substituted.
The solution indicates that the magnitude of the electric …eld is independent of the distance from the sheet. The direction of the electric …eld is negative in the region z <0, and positive for
z >0. When there are two oppositely charged sheets, and (C/m2), the electric …eld outside
the sheets if zero, but the …eld in between the sheets is given by,
Ez =
0
(1.24) as can be readily seen from the principle of superposition. This con…guration corresponds to a parallel plate capacitor provided the edge e¤ects are ignored.
Line Charge
We assume a long line charge with a line charge density (C/m). At a distancer from the line charge, the di¤erential electric …eld due to a charge dq= dz located at z is
dE= 1 4 0
dz
r2+z2 (cos er+ sin ez) (1.25)
where,
cos = p r
r2+z2; sin =
z
p
r2+z2
The zcomponent is an odd function ofz. Therefore, the zcomponent of the electric …eld vanishes after integration from z= 1 to+1. The radial (r) component remains …nite, and is given by,
Er = 4 0
Z 1
1
r
(r2+z2)3=2dz= 2 0r (1.26)
Remember that this result is valid only if the line charge is long, or the point of observation is su¢ ciently close to a line charge of …nite length.
1.5
Gauss’Law for Static Electric Field
The electric …eld at a distance rfrom a point charge q is,
E= 1 4 0
q r2er;
charge
sheet
σ
(C/m
2)
E =
σ/2ε
0E =
σ/2ε
0σ
−σ
E = 0
E = 0
E =
σ/ε
0Figure 1-5: Upper …gure: Single charge sheet. The electric …eld on both sides isEz = =2"0:Lower
…gure: Equal, opposite charge sheets. The …eld in-between is Ez = ="0: Outside,Ez = 0:
r
z
dq=
λ
dz
dE
dE
dE
z
r
z
line charge
Figure 1-6: Electric …eld due to a long line charge (line charge density C/m). Note thatEz = 0
and the radial electric …eld Er= 2 "0r
b
a r
θ
γ
q
dEn
Figure 1-7: Gauss’law applied to a sphere that is not concentric with the charge. Note rcos + bcos =a:
On a spherical surface with radiusr, the magnitude of the electric …eld is constant, and the quantity,
4 r2Er
is equal to q= 0. This strongly suggests that the closed surface integral of the electric …eld,
I S
EdS (1.27)
is equal to the amount of charge enclosed by the closed surface S divided by 0,
I S
EdS=q "0
Noting I
S
EdS= Z
r EdV
and
q= Z
(r)dV
we …nd the Maxwell’s equation
r E=
"0
Let us see if this is the case for a spherical surface which is not concentric with the point charge
q. We denote the distance between the charge and the spherical center by b, and the radius of the sphere by a.
the relationship,
r2 =a2+b2 2abcos
in Fig. ??, we …nd the magnitude of the electric …eld at angle ,
E = q 4 0
1
a2+b2 2abcos (1.28)
The component normal to the spherical surface isEcos where the angle is related to through
rcos +bcos =a:
Therefore, the entire surface integral reduces to,
I S
E dS= q 4 0
Z
0
a bcos
(a2+b2 2abcos )3=22 a
2sin d (1.29)
where
dS= 2 a2sin d
is the area of the ring having radius asin and width ad . The relevant integral is
Z
0
(a bcos ) sin
(a2+b2 2abcos )3=2d =
8 < :
2
a2; a > b
0; a < b
(1.30)
(In integration, it is convenient to change the variable from to through = cos . Then the integral reduces to
R1 1
a b
(a2+b2 2ab )3=2d
= 1
bpa2+b2 2ab 1
1
1 a2b
a2+b2 ab p
a2+b2 2ab 1
1
Evaluation of the de…nite integral is left for a mathematical exercise. Note thatp(a b)2 =ja bj.)
Therefore, the surface integral of the electric …eld becomes,
I
EdS= 8 < :
q
0
; a > b 0; a < b
(1.31)
Obviously, the case a > bcorresponds to a sphere enclosing the charge, and a < b corresponds to the case in which the charge is outside the closed spherical surface. The result may be generalized to a closed surface of an arbitrary shape. The following formula is called Gauss’law,
0
I S
EdS=q Total charge
enclosed by S
!
Again, remember that Gauss’ law is equivalent to Coulomb’s law, since we have “deduced” the former from the latter. In fact, Gauss’law can be mathematically “proven”if we adopt Coulomb’s law. A formal proof will be given after the Maxwell’s equation is introduced.
Gauss’law can be convenient for simple cases in which a system has a high degree of symmetry, such as spherical, cylindrical, and planar symmetries. Let us work on a few simple examples. Uniformly-Charged Insulating Sphere
Let an insulating sphere of radiusacarry a uniform charge density (C/m3) and a total charge
q = 43 a3 (C). The system has complete spherical symmetry, and the only nonvanishing component of the electric …eld is the radial component, Er. Outside the sphere (r > a), Gauss’law yields,
4 r2Er= q
0
or
Er = q 4 0
= a
3
3 0r2
(1.33) which is identical to the …eld due to a point charge q concentrated at the center. Inside the sphere (r < a), Gauss’law reads
4 r2Er= 1
0
4 3 r
3 (1.34)
since in the RHS, only the amount of charge enclosed by the spherical surface (called Gaussian surface) having a radius r (< a) enters. Solving for Er, we obtain,
Er= 3 0
r (1.35)
Therefore, in the sphere, the …eld linearly increases with the radiusrup to the surface,r =a, where the interior …eld connects to the exterior …eld without dicontinuity. The electric …eld is maximum at the surface as shown in Fig. 1-8.
The fact that the electric …eld should vanish at the center of a charged (uniformly!) sphere is understandable from spherical symmetry. At the center, the contribution from a charge dq to the electric …eld can always be cancelled by another located opposite with respect to the center. By analogy, the gravitational …eld due to the earth mass itself at the earth’s center should be zero. Charged Conducting Sphere
A charge given to a conductor must reside entirely on the conductor surface so that the electric …eld inside a conductor body should be identically zero in static condition. If an electric …eld were not zero in a conductor, a large electric current would ‡ow according to Ohm’s law,
J= E (1.36)
where (Siemens/m) is the conductivity. of metals is large. (For example, copper has '
5:9 107 S/m). Therefore, unless E = 0 in a conductor, a large current should ‡ow, and this violates the assumption of static electricity. In other words, an electric …eld can exist in a conductor
r Er
a 2a 3a 4a
Emax
a
ρ
Figure 1-8: Electric …eld of a unifrmly charged sphere. The …eld is 0 at the center. The maximum …eld,Emax=
a 3"0
;occurs at the surface.
only in dynamic conditions in which current ‡ow is allowed.
If an excess chargeq is given to a conducting sphere, the charge uniformly resides on the surface as a surface charge, with a surface charge density s=q=4 a2(C/m2) whereais the sphere radius. The electric …eld inside (r < a) the sphere is zero, while outside (r > a), it is given by
Er= 1 4 0
q
r2 (r > a) (1.37)
Note that there is a sudden jump in the …eld at the surface (r =a) where the surface charge density exists. In general, wherever an in…nitesimaly thin surface charge layer exists, the electric …eld there becomes discontinuous. We will come back to this subject in Chapter 3 where the concept of the displacement vector D is introduced.
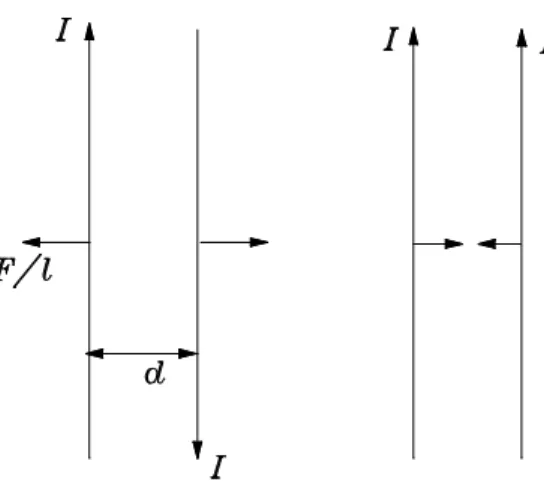
Experimental Veri…cation of Coulomb’s Inverse Square Law
As stated earlier, Gauss’law and Coulomb’s law are physically identical, in the sense that the former is derivable from the latter. Therefore, if Gauss’ law can be veri…ed experimentally, then Coulomb’s law is indirectly veri…ed also. Here, we are particularly concerned with a question: How valid is the inverse square law? Or put alternatively, when the Coulomb’s law is written as
F= const: rn er
r Er
a 2a 3a 4a
Emax
a
σ
conducting sphere carrying a surface charge
Figure 1-9: Electric …eld in a charged conducting sphere is 0. The charge q given to the sphere must reside on the surface as a surface charge =q=4 a2 C/m2:
indeed very close to 2.0 with an uncertainty of order 10 16. The powernis probably exactly equal
to 2.
The experiment performed by Plimpton and Lawton in 1936 was to measure the intensity of electric …eld inside a charged conducting shell. As we have just seen in the preceding example, an excess charge given to a conductor must reside entirely on its outer surface, and the electric …eld in the conductor must be zero. This holds for a conducting shell, too, and no charge can exist on the inner surface of the shell. Plimpton and Lawton establishedn= 2 2 10 9. Further improvement
n= 2 2 10 16 was achieved later in 1971 by Williamset al.
1.6
Di¤erential Equations for Static Electric Fields-Maxwell’s
Equa-tions
For a given charge distribution (r), the electric …eld can be uniquely evaluated from
E(r) = 1 4 0
Z r r0
jr r0j3 (r
0)dV0 (1.38)
as we have seen in Sec. 1.4. The electric …eld also satis…es Gauss’law,
I S
EdS= 1
0
Z V
We may use either formulation in evaluating the electric …eld due to a prescribed charge distribution. The electric …eld is a vector quantity. A vector can be uniquely de…ned if its divergence and curl are both speci…ed. This mathematical theorem is known as Kirchho¤’s theorem. (Kirchho¤ is a familiar name in electric circuit theory. However, his contributions are not limited to circuit theory, but quite diversi…ed. Kirchho¤’s scalar di¤raction formula for electromagnetic waves is another important contribution, and had been used extensively until it was replaced by a more accurate vector di¤raction formula rather recently. See Chapter 13.) A derivation of vector di¤er-ential equations for electric and magnetic …elds was formulated by Maxwell in the celebrated book “Treatise on Electricity and Magnetism” published in 1873. Each …eld (electric and magnetic) requires both divergence and curl. Therefore, for complete description of electric and magnetic …elds, four Maxwell’s equations emerge.
In electrostatics, the magnetic …eld is absent (or ignored). Let us start with the divergence of static electric …elds. In the example of a charged sphere in Sec. 2.5, we have seen that the electric …eld inside a uniformly charged spherical body can be found from Gauss’law,
4 r2Er= 1
0
4 3 r
3 (1.40)
with the result,
Er= 3 0
r (1.41)
Eq. (1.40) holds no matter how small r is chosen. The divergence of the electric …eld is de…ned by
div E=r E= lim V!0
H
SE dS
V (1.42)
In Eq. (1.40), the LHS is a special case of symmetric surface integration, and the quantity 4 r3=3
in the RHS is of course the volume. Therefore, if we take the limit of r!0 in the ratio,
lim r!0
4 r2Er
4 3 r3
it reduces to the de…nition of divergence. Consequently, the divergence of the electric …eld satis…es,
r E=
0
(1.43) This is one of Maxwell’s four equations.,
Outside the charged sphere, the surface integration,
I S
E dS
vanishes unless S intersects the sphere. Therefore, outside the sphere, r E = 0, as required because = 0 outside the sphere.
less clear. The surface integral can be rewritten in terms of a volume integral as follows,
I S
EdS= Z
V r
EdV (Gauss’theorem) (1.44)
This is a mathematical theorem, and has nothing to do with the physical Gauss’law, although they are intimately related. Using this transformation, we can rewrite Gauss’law as,
Z
r EdV = 1
0
Z
dV (1.45)
Therefore, r E= = 0 immediately follows.
The third method to derive the divergence equation for the electric …eld is to directly take the divergence of Eq. (1.18),
rr E(r) = 1 4 0rr
Z r r0
jr r0j3 (r
0)dV0 (1.46)
where the subscript r indicates di¤erentiation with respect to the observer’s coordinates r. The function,
rr
r r0
jr r0j3 (1.47)
has a peculiar property. It vanishes wherever r6=r0 but is not properly de…ned where r=r0. (In fact, it diverges atr=r0.) Introducing jr r0j=R, we indeed see that,
rr
r r0
jr r0j3 =
1 R2
d dR R
2 1
R2 = 0 (R6= 0)
However, its volume integral is well de…ned and remains …nite since
R
rr
r r0
jr r0j3 dV
=
I r r0
jr r0j3 dS
= I 1
R2R 2d =
I
d = 4 (1.48)
whered is the di¤erential solid angle, and4 is the total solid angle. In other words, the function,
rr
r r0
jr r0j3 (1.49)
has the property of the delta function,
rr
r r0
jr r0j3 = 4 (r r
where
(r r0) = (x x0) (y y0) (z z0) (1.51) is the three-dimensional delta function having the dimensions of m 3. Therefore, the integral in
Eq. (1.46) can be readily performed as
4 4 0
Z
(r0) (r r0)dV0 = 1
0
(r) (1.52)
and Eq. (1.46) is equivalent to
r E= 1
0
(1.53) We now evaluate the curl of a static electric …eld given in Eq. (1.18). Taking the curl of both sides, we …nd,
rr E(r) = 1 4 0
Z
rr
r r0
jr r0j3 (r
0)dV0 (1.54)
However, in the RHS, the vector,
rr
r r0
jr r0j3 =rr
1
jr r0j3 (r r
0) + 1
jr r0j3rr (r r
0) (1.55)
identically vanishes, because the vector,
rr 1
jr r0j3 = 3
r r0
jr r0j4 (1.56)
is parallel to the vectorr r0, and
rr (r r0) 0 (1.57)
identically. In contrast to the divergence in Eq. (1.46),
rr
r r0
jr r0j3 0 (1.58)
holds even atr r0= 0. Therefore, for static electric …elds due to charge distributions, we conclude,
r E= 0 (1.59)
We thus have speci…ed both divergence and curl of static electric …elds in Eqs. (1.53) and (1.59), respectively, which determine static electric …elds (vector) uniquely. The divergence equation holds for any electric …elds (electrostatic and non-electrostatic), but the curl equation is the special case of the more general Maxwell’s equation,
r E= @B
@t (1.60)
What are the physical meanings of the Maxwell’s equations? The nonvanishing divergence of the static electric …eld indicates that the charge density is the source (or sink) of the …eld. This may be illustrated by the electric lines of force. A positive charge “emits” electric …eld lines, while a negative charge “absorbs”electric lines of force, just like stream lines in water ‡ow. If two equal, but opposite charges are near by, the …eld lines “emitted”by the positive charge are all “absorbed” by the negative charge. If the magnitude of the charges are not equal, some …eld lines are not absorbed by the negative charge.
The vanishing curl of static electric …elds indicates that an electric …eld line does not close on itself, that is, a …eld line does not form a loop. (This is in contrast to non-electrostatic …eld for which the curl is nonvanishing.) In other words, static electric …eld lines always have heads or tails as clearly seen in the above examples. Static …eld lines start at a positive charge and end at a negative charge.
1.7
Scalar Potential
(
r
)
The vanishing curl of static electric …elds has an important implication. Since the curl of a gradient of an arbitrary scalar function is identically zero,
r rF 0 (1.61)
a static electric …eld (vector!) can be deduced from a gradient of some scalar function. We denote this scalar by (r) and call it a scalar potential. The electric …eld is given by the gradient of the scalar potential,
E(r) = r (r) (1.62)
The negative sign is introduced so that the electric …eld is directed from higher to lower potential regions, just like in the familiar gravitational …eld and gravitational potential.
The dimensions of the scalar potential are Newton meter
Coulomb =
Joule Coulomb
This is rede…ned as Volts (after Volta). Therefore, an alternative unit for the electric …eld is Volts/meter.
The physical meaning of the electric …eld is (as discussed before) the force to act on a unit charge. Then, the scalar potential can be interpreted as the work required to move a unit charge from one point to another, since
(r) = (r1)
Z r
r1
E dr (1.63)
where (r1) is the potential at r1 . Clearly, the potential is a relative quantity and is referred
V
d E
x
0 d
Φ (x)
V
Figure 1-10: Potential (x) = V
dx and electric …eld Ex= V =d in a parallel plate capacitor.
should be recalled. When we measure the height of a mountain, usually the sea level is chosen as the reference point.)
As an example, let us consider a point charge q placed at the originr = 0. The electric …eld is given by,
Er(r) = 1 4 0
q
r2; V/m
If the reference potential = 0is chosen on a surface with a radiusr1, the potential at an arbitrary
point r becomes
(r) = Z r
r1
q 4 0
1 r2dr
= q
4 0
1 r
1 r1
(1.64) For a charge system of a …nite spatial extent, it is convenient to choose = 0 atr1=1, so that
(r) = 1 4 0
q
r; (V) (1.65)
relative to the zero potential at r=1.
Similarly, the potential due to a charged conducting sphere with a total charge q and radiusa
is given by,
(r) = 1 4 0
q
relative to = 0 atr=1. The sphere potential can be found by equating the radius to r=a,
sphere= 1 4 0
q
a (1.67)
Note that this result is independent of whether the conducting sphere is solid or shell, since the electric …eld in the conductor must vanish identically. In general, the potentials at any points on and in a conductor must be equal because E = 0 in a conductor. In particular, the surface of a conductor, no matter how complicated is its shape, is an equipotential surface. This fact will play an important role in potential boundary problems in Chapter III.
In the following, we will work on a few examples in which the potentials can be calculated from known electric …elds.
Potential of a Charged Insulating Sphere
The electric …eld for this problem has been worked out in Sec. 1.5, and given by
Er = 8 > > > < > > > :
3 0
a3
r2; (r > a)
3 0
r; (r < a)
(1.68)
where is the charge density and a is the sphere radius. We choose = 0 atr =1. Then, the exterior potential becomes
(r) = Z r
13 0
a3 r2dr
= 3 0
a3
r ; (r > a) (1.69)
On the surface of the sphere, the potential takes the value,
(a) = 3 a
2 (1.70)
Therefore, the interior potential becomes,
(r) = (a) Z r
a 3 0
rdr
= a
2
3 0 6 0
r2 a2
= a
2
2 0 6 0
r2; (r < a) (1.71)
The potential at the sphere center is ,
(r= 0) = a
2
2 0
(1.72) which is the maximum (ifq >0) potential. Note that the integration should be carried out starting
at the reference point (r =1 in this case), and radially inward. Potential due to a Long Line Charge
The electric …eld due to a long line charge has been found in Section 1.5, and given by
E = 2 0
1
(1.73) where (C/m) is the line charge density. Let us choose a reference, zero potential surface at a radius =a. (acannot be in…nity, in contrast to the case of spheres, because the potential due to an in…nitely long line charge does not vanish at in…nity, but diverges. Such a line charge requires in…nitely large amount of energy, and thus is of mathematical interest only.) Then, the potential at an arbitrary radial position can be found as
( ) = Z
a E d =
2 0
Z a1 d =
2 0
ln a (1.74)
The zero potential surface can be chosen arbitrarily, since the potential is a relative quantity. However, the potential di¤erence between two radial positions is independent of the choice of the reference. Indeed, the potential di¤erence between two points at 1 and 2 becomes
( 1) ( 2) = 2 0
ln a
1
ln a
2
= 2 0
ln 2
1
(1.75) in which the particular radius ahas disappeared.
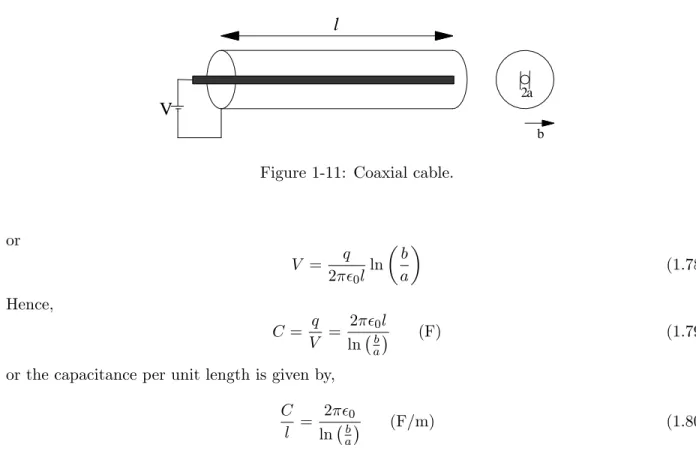
In practical applications, the potential we just found can be used to calculate the capacitance of a coaxial cable. Let us consider a coaxial cable having inner and outer conductor radii aand b, respectively, as shown in Fig. 1-11. We connect a dc power supply of a voltage V between the two conductors. If we can calculate the charges qto appear on respective conductors, the capacitance can be calculated by de…nition from,
C = q
V (F) (1.76)
The charge per unit length is,
= q
l (1.77)
Therefore, the potential di¤erence between the two conductors becomes,
V = (a) (b) = 2 0
ln b a
V
2a
b
l
Figure 1-11: Coaxial cable.
or
V = q 2 0l
ln b
a (1.78)
Hence,
C= q V =
2 0l
ln ba (F) (1.79)
or the capacitance per unit length is given by,
C l =
2 0
ln ab (F/m) (1.80)
If the space between the conductors is …lled with a dielectric having a permittivity , this should be modi…ed as
C l =
2
ln ab (1.81)
1.8
Potential due to a Prescribed Charge Distribution
In the preceding Section, we have (brie‡y) learned how to calculate the potential (r)from a known electric …eld. However, in most applications, it is more common to reverse the procedure, namely, we …rst …nd the potential , and then calculate the electric …eld from,
E= r (1.82)
There are several reasons for inverting the procedure. The basic Maxwell’s equations for static electric …elds are,
rE=
0
(1.83)
Obviously, these are vector di¤erential equations, and for a complete solution, we must solve three di¤erential equations for each component of the …eld E. However, if we substitute
E= r
into rE=
0
, we …nd a single scalar di¤erential equation for ,
r2 =
0
(1.85) This is known as Poisson’s equation, and mathematically speaking, it is an inhomogeneous version of the Laplace equation,
r2 = 0 (1.86)
for which exhaustive studies have been made since the 18th century. The Laplace and Poisson’s equations most frequently appear in physical science and engineering. Analytic solutions to those equations can be found in a relatively limited number of cases. However, with powerful computers becoming more easily accessible these days, numerical solutions to Poisson and Laplace equations are no more prohibitively expensive even for complicated geometries for which analytic solutions are extremely di¢ cult, if not impossible. We will return to the problem of solving Laplace equations in the following Chapter. Here, we derive a formal solution to the Poisson’s equation, which enables us to calculate the potential for a prescribed charge distribution.
There are several methods to …nd the solution to
r2 =
0
and we start with a method that is physically most transparent. We have already seen that the potential due to a point charge q is given by
(r r0) = q 4 0
1
jr r0j (1.87)
where r0 is the location of the point charge.
For a distributed charge, we pick up a small volumedV0 in the region where the charge density, , exists. The charge contained in the volumedV0 is
dq= dV0 (1.88)
By choosing the volumedV0 su¢ ciently small, the di¤erential chargedq approaches a point charge. Therefore, the potential due to the charge dq located at r0 becomes
d = 1 4 0
(r0)
jr r0j dV
r'
r
r - r'
dq
O
d
Φ
provided the reference potential = 0 is at r = 1. By integrating Eq. (??) over the dummy variable r0, we …nd
(r) = 1 4 0
Z (r0)
jr r0j dV0 (1.90)
which is the desired solution to the Poisson’s equation.
The same result can be deduced from the electric …eld due to a prescribed charge distribution found earlier,
E(r) = 1 4 0
Z r r0
jr r0j3 (r0)dV0:
Since
r r0
jr r0j3 = rr
1
jr r0j
where the subscript r indicates di¤erentiation with respect to the observing point r, we …nd
E(r) = 1 4 0r
r
Z (r0)
jr r0j dV0 (1.91)
Note that the di¤erential operator rr can be taken out of the integral, because it operates on r
only. Comparing with the basic relationship,
E= r
we readily obtain
(r) = 1 4 0
Z
(r0)
jr r0j dV0
which is identical to Eq. (1.90). Below, we will apply this formula to a few simple problems. Potential due to a Line Charge of Finite Length
z
z'
dq
d
Φ
a
-a
ρ
Figure 1-12: Line charge( C/m)of …nite length2a: dq = dz0:
charge dq= dz0 located at z0 creates a potential at the coordinates( ; z),
d = 1 4 0
dz0 p 2
+ (z z0)2 (1.92)
Integrating this over z0 from z0 = ato+a, we …nd
( ; z) = 4 0
Z a a
dz0 p
(z0 z)2+ 2
= 4 0
h
ln p(z0 z)2+ 2+z0 z ia
a
= 4 0
ln p
(z a)2+ 2+a z
p
(z+a)2+ 2 a z
!
(1.93)
Let us examine special cases of the potential. At a point very close to the line charge, so that
z!0, and a, the potential reduces to
( )' 2 0
ln 2a ( a) (1.94)
The potential of the form
( ) =
2 0
ln + const. (1.95)
has been worked out in Sec. 2.6 for a long coaxial cable, and the result we just obtained is therefore of an expected form.
point charge, q = 2a . On the plane z= 0, the logarithmic function approaches
ln p 2
+a2+a
p 2
+a2 a
!
'ln 1 + 2a ' 2a ( a) (1.96)
Therefore, the potential indeed approaches
( )' q 4 0
1
( a) (1.97)
where q = 2a is the total charge carried by the line. On the z axis, ! 0, and at jzj a, the potential also approaches,
(z) = 4 0
lim
!0ln
p
(z a)2+ 2+a z
p
(z+a)2+ 2 a z
!
= 4 0
ln 1 +2a z
' 4q
0
1
z (1.98)
Capacitance of a Thin Linear Conductor
The expression for the potential in the vicinity of a line charge, Eq. (1.94), can be directly used to …nd the capacitance of a thin linear conductor having a radius band length 2awith a b. On the surface of the conductor, =b. Therefore, the potential of the conductor can be approximated by
( = b) = 2 0
ln 2a b
' 4 q
0a
ln 2a b
and the approximate capacitance is given by
C = 4 0a=ln
2a b = 2 "0L
ln(L=b) (1.99)
where L= 2ais the total length of the conductor. Capacitance of Parallel Wire Transmission Line
As an application of the potential due to a line charge, we consider a long, two-parallel-wire transmission line, which is often encountered in high voltage power transmission and old-fashioned telephone lines. The geometry is shown in Fig. ??. We assume two thin parallel conductor wires
of an equal radius aseparated a distanced. By “thin conductor wires”, we meand a. Since the capacitance we are concerned here is the mutual capacitance between the two wires, we let the two wires carry equal, but opposite line charge densities, + and (C/m). Then, the potential at arbitrary point can be written down as
(r+; r ) =
2 0
[ lnr++ lnr ]
= 2 0
ln r r+
where r+ and r are the distance from the observing point to the positive and negative wires,
respectively. Note that the reference, zero potential surface is chosen at the midplane on which
r+=r .
When the wire radius ais small compared with the separation distance d, the potential at the surface of the positive wire can be found by letting r+=aand r =d,
+=
2 0
ln d
a (1.100)
Similarly, the potential at the negative wire is,
= 2 0
a
d = 2 0
ln d
a (1.101)
Therefore, the potential di¤erence between the wires is
V = + =
0
ln d
a (1.102)
and the capacitance per unit length of the transmission line is given by,
C
l = V = 0=ln d
a (F/m) (1.103)
The capacitance (per unit length) of a single wire transmission line placed above the ground at a height h can be found in a similar manner. The ground potential can be chosen to be zero. Therefore, the potential di¤erence between the wire and the ground is given by
V = 2 0
ln 2h
a (1.104)
where 2h is the distance between the wire and an image line charge located at the mirror point,
z= h, in the ground. Then, the capacitance becomes
C
l = 2 0=ln 2h
+λ
r
−λ
r
+
-d
Figure 1-13: Parallel wire transmission line. Separation distance dand wire radiusa:
Note that this is twice as large compared with the capacitance of the two-wire transmission line. The latter can be considered to be a series connection of two capacitors, one between the positive wire and the midplane, and the other between the negative wire and the midplane. The midplane, which is chosen at zero potential, can be replaced by a grounded large conducting plate without a¤ecting the potential and electric …eld. The method of images will be discussed more fully in Chapter 5.
Both formulae in Eqs. (1.103) and (1.105) are subject to the assumption of thin wire radius,
a d; h. As the wire radius becomes large, they become inaccurate, but only logarithmically. For example, the exact capacitance of the parallel wire transmission line is given by
C l = 0
1 ln
"
d+pd2 4a2
2a
# (1.106)
Even when a= 0:2d(thick conductors indeed), the error caused by using the approximate formula in Eq. (1.103) is less than 3%.
Electric Dipoles
Two charges of opposite signs, but equal magnitude,+q and q separated by a small distance
a constitute an electric dipole. (A single charge q is called a monopole. Higher order multipoles, quadrupole, octapoles, etc., can be similarly constructed.) Dipoles are the basic elements in dielec-tric materials as we will study in detail in Chapter 4.
jsin j
The potential due to two charges, +q and q, can be written down as
(r+; r ) =
q 4 0
1 r+
1
Φ
+q
-q
a
θ
r
r
+
−
Figure 1-14: Electric dipole consists of two charges q and q separated by a small distance a:
where r+ and r are the distances to the respective charges from the observation point. They are
related through
r2+=r2 +a2 2ar cos (1.108)
where is the angle between the z axis and the vectorr . So far, we have not made any approxi-mations, and Eq. (??) is exact.
At a point far away from the dipole such that r+; r a, r+ may be approximated by
r+'r acos (1.109)
Then, the potential at r abecomes
(r; ) = q 4 0
1 r acos
1 r
' 4q
0
acos
r2 (1.110)
where we have replaced r ('r+) by r. In contrast to the monopole potential,
(r) = 1 4 0
q r
the dipole potential is proportional to 1=r2, and thus of higher order in the series expansion in
powers of1=r. The potentials due to the equal but opposite charges cancel each other in the lowest (monopole) order. Also, the dipole potential has the angular dependence,cos . It is convenient to introduce the dipole moment (vector)
-0.6 -0.4 -0.2 0.2 0.4 0.6
-1.0 -0.8 -0.6 -0.4 -0.2 0.2 0.4 0.6 0.8 1.0
x
y
Figure 1-15: Equipotential surfaces of electric dipolepz:
where a is the vector directed from the negative charge q to the positive charge +q. Since is the angle between aand r, we may rewrite Eq. (1.110) as
= 1 4 0
p r
r3 (1.112)
where
p r=prcos =aqrcos
The equipotential surface of the dipole is shown in Fig. 1.17.
p
jsin j
The electric …eld associated with the dipole can be calculated by taking the gradient of the potential,
E = r (r; ) = er
@ @r +
e r
@ @
1 4 0
aq r2 cos
= aq 4 0
2
r3 cos er+
sin
The electric …eld lines are described by the following di¤erential equation,
dr Er
= rd
E (1.114)
since the electric …eld is tangent to the …eld lines. The components, Er andE are Er =
aq 4 0
2
r3 cos (1.115)
E = aq 4 0
1 r3 sin
Substituting these into Eq. (??), we …nd the following di¤erential equation to describe the …eld line,
dr= 2rcot d
or
dr
r = 2 cot d (1.116)
Integrating both sides, we obtain
lnr= ln(csin2 ) (1.117)
or
r=csin2
where c is a constant. The electric …eld lines of the diople are shown in Fig. 1.18. Note that the electric …eld lines are normal to the equi potential surfaces.
cos2
1.9
Linear Quadrupole
Charges +q; 2q; and +q placed along the z axis atz=a; 0; aconstitute a linear quadrupole. The potential at r a can be found as superposition of 3 potemtials,
(r; ) = q 4 "0
1
p
r2+a2 2arcos
2 r +
1
p
r2+a2+ 2arcos
' qa
2
4 "0
3 cos2 1 r3
where use is made of binomial expansion
1
p
1 +x = 1 1 2x+
3 8x
-1.0 -0.8 -0.6 -0.4 -0.2 0.2 0.4 0.6 0.8 1.0
-0.3 -0.2 -0.1 0.1 0.2 0.3
x
y
Figure 1-16: Electrif …eld lines of the dioplepz =qa:
Note that the dipole potemtial vanishes. This is because the quadrupole consists of two dipoles oppositely directed. The equipotebtial surfaces of the linear quadrupole is shown in Fig. 1.
1 3 sin2
-1.0 -0.5 0.5 1.0
-2 -1 1 2
x
y
The function
P2(x) =
1 2 3x
2 1
charge q atz=ais
1 =
q 4 "0
1
p
r2+a2 2arcos
= q
4 "0
1 r +
a
r2cos +
a2 r3
3 cos2
2 +
= q
4 "0
1
X l=0
al
rl+1Pl(cos )
Likewise
2 =
q 4 "0
1
p
r2+a2+ 2arcos
= q
4 "0
1
X l=0
( 1)l a l