Graphing formulas: unraveling experts’ recognition processes

Peter

M.G.M.

Kop

_,

_Fred

_J.J.M.

_Janssen

_,

_Paul

_H.M.

_Drijvers

_,

_Jan

_H.

_van

_Driel

a_{Iclon,LeidenUniversity,TheNetherlands}

b_{FreudenthalInstitute,UtrechtUniversity,TheNetherlands}

c_{MelbourneGraduateSchoolofEducation,TheUniversityofMelbourne,Australia}

a

r

t

i

c

l

e

i

n

f

o

Articlehistory:

Received10June2016

Receivedinrevisedform12January2017 Accepted25January2017

Availableonline9February2017

Keywords:

Graphingformulas Experts’recognition Functionfamilies Prototypesandattributes

a

b

s

t

r

a

c

t

Aninstantlygraphableformula(IGF)isaformulathatapersoncaninstantlyvisualize usingagraph.TheseIGFsarepersonalandserveasbuildingblocksforgraphingformulas byhand.Thequestionsaddressedinthispaperarewhatexperts’repertoiresofIGFsareand whatexpertsattendtowhilerecognizingtheseformulas.Threetasksweredesignedand administeredtofiveexperts.Thedataanalysis,whichwasbasedonBarsalouandSchwarz andHershkowitz,showedthatexperts’repertoiresofIGFscouldbedescribedusingfunction familiesthatreflectthebasicfunctionsinsecondaryschoolcurriculaandrevealedthat experts’recognitioncouldbedescribedintermsofprototype,attribute,andpart-whole reasoning.Wegivesuggestionsforteachinggraphingformulastostudents.

©2017ElsevierInc.Allrightsreserved.

1. Introduction

Algebraicconcepts,likefunctions,canbeexploredmoredeeplythroughlinkingdifferentrepresentations(Duval,2006;

Heid,Thomas,&Zbiek,2012).Graphsandalgebraicformulasareimportantrepresentationsoffunctions.Graphsseemtobe

moreaccessiblethanformulas(Leinhardt,Zaslavsky,&Stein,1990;Moschkovich,Schoenfeld,&Arcavi,1993).Inaddition, graphsgivemoredirectinformationoncovariation,thatis,howthedependentvariablechangesasaresultofchangesof theindependentvariable(Carlson,Jacobs,Coe,Larsen,&Hsu,2002).Agraphshowsfeaturessuchassymmetry,intervals ofincreaseordecrease,turningpoints,andinfinitybehavior.Inthisway,itvisualizesthe“story”thatanalgebraicformula tells.Thereforegraphsareimportantinlearningalgebra,inparticularinlearningtoreadalgebraicformulas(Eisenberg&

Dreyfus,1994;Kieran,2006;Kilpatrick&Izsak,2008;NCTM,2000;Sfard&Linchevski,1994).

Studentshavedifficultiesinseeingafunctionbothasaninput-outputmachineandasanobject(Ayalon,Watson,&

Lerman,2015;Gray&Tall,1994;Oehrtman,Carlson,&Thompson,2008;Sfard,1991).Graphsappealtoagestalt-producing

ability,andinthiswaycanhelptoconsolidatethefunctionalrelationshipintoagraphicalentity(Kieran,2006;Moschkovich etal.,1993).Graphsarealsoconsideredimportantinproblemsolving.Graphsareusedforunderstandingtheproblem situation,recordinginformation,exploring,andmonitoringandevaluatingresults(Polya,1945;Stylianou&Silver,2004).

So,theabilitytoswitchbetweenrepresentations,representationversatility,inparticularconversionsfromalgebraic formulastographs,isimportantinunderstandingalgebraandinproblemsolving(Duval,2006;NCTM,2000;Stylianou,

2011;Thomas,Wilson,Corballis,Lim,&Yoon,2010).

∗ Correspondingauthor.

E-mailaddress:koppmgm@iclon.leidenuniv.nl(P.M.G.M.Kop).

http://dx.doi.org/10.1016/j.jmathb.2017.01.002

Inapreviousstudyaframeworkwasdevelopedtodescribestrategiesforgraphingformulaswithoutusingtechnology

(Kop,Janssen,Drijvers,Veenman,&VanDriel,2015).Intheframework,itisindicatedhowrecognitionguidesheuristic

search.Whenonehastographaformulatherearedifferentpossiblelevelsofrecognition:fromcompleterecognition(one immediatelyknowsthegraph)tonorecognitionatall(onedoesnotknowanythingaboutthegraph).Foreverylevelof recognitiontheframeworkprovidesstrongtoweakheuristics.

Forthetwohighestlevelsofrecognitionthegraphiscompletelyrecognizedortheformulaisrecognizedasamemberof afunctionfamilywhosegraphcharacteristicsareknown.Forinstance,atthehighestlevelofrecognitionthegraphofy=x2

isinstantlyrecognizedasaparabolawithminimum(0,0).Atthesecondlevelofrecognition,y=4·0.75x_{+3isrecognizedas}

amemberofthefamilyofdecreasingexponentialfunctions,andsothehorizontalasymptoteisreadfromtheformula.In thiswaythegraphcanbeinstantlyvisualized.Anotherexampleatthislevel:y=−x4_+6x2_{isrecognizedasapolynomial}

functionofdegree4;becauseofthenegativeheadcoefficientitsgraphhasanM-shapeoran-shape;ashortinvestigation of,forinstance,thezeroeswillinstantlygivethegraph.

Atthesetwohighestlevelsofrecognitionintheframework,formulascanbeinstantlylinkedtographs.Therefore,these formulasaredefinedasinstantlygraphableformulas(IGF).AlargesetofIGFsisbeneficialtoproficiencyingraphingformulas. Thecurrentstudywasfocusedonexperts’recognitionprocesseswhendealingwithIGFs.Forthisstudywedefinedanexpert asapersonwithatleastamaster’sdegreeinmathematicsandatleast10yearsofexperienceteachingatthesecondary orcollegelevel,withexperienceingraphingformulasbyhand.Althoughtheseexpertsareexpectedtobeabletoinstantly linkmanyformulastographs,theirrepertoiresofIGFsremainunknown.Inaddition,weinvestigatedwhatexpertsattend towhenrecognizingIGFs.ThisinformationmightgivesuggestionsforarepertoireofIGFsforstudentsandforafocusin teachingstudentsIGFs.

2. Theory

2.1. Cognitiveunitsasbuildingblocks

IGFscanbeseenasbuildingblocksinthinkingandreasoningwithandaboutformulasandgraphs.BarnardandTall(1997)

introducedtheconceptof“cognitiveunit”,anelementofcognitiveknowledgethatcanbethefocusofattentionaltogether atonetime.Forexperts,well-connectedcognitiveunitscanbecompressedintoanewsinglecognitiveunitwhichcan beusedasjustonestepinathinkingprocess(Crowley&Tall,1999).Inthiswayexperts’knowledgeiswellorganizedin hierarchicalmentalnetworkswithcomplexcognitiveunits,whichcanbeenlistedwhennecessary(Campitelli&Gobet,

2010;Chi,Feltovich,&Glaser,1981;Chi,2011).

AsIGFsarecognitiveunitsingraphingformulas,theycanbecombined(addition,multiplication,chaining,etc.)andcan formnew,morecomplexIGFs.Forinstance,whendealingwithy=−x4_+6x2_{,novicesmayrecognizetheIGFsy=−x}4_and y=6x2_{andhavetocombinethesetwoIGFstodrawagraph,whereasy=−x}4_+6x2_{isanIGFforexperts,whorecognizea}

4thdegreepolynomialfunction.Forexperts,aformulalikey=x2_{−6x+5cantriggerothercognitiveunits,like“itsgraph}

isaparabolawithaminimumvalue”,andtheequivalentformulasy=(x−1)(x−5) andy=(x−3)2−4,whichcangive informationaboutthezeroesandtheminimumvalue,etc.Expertsareexpectedtohavemore,andmorecomplex,IGFsthan novices,whichgenerallyenablethemtographformulaswithfewerdemandsontheworkingmemory(Sweller,1994).

Thecurrentstudywasfocusedonrecognition:inparticular,whichformulasand/orfunctionfamilieswereinstantly recognizedbyexpertsandhowtherecognitionprocessescanbedescribed.

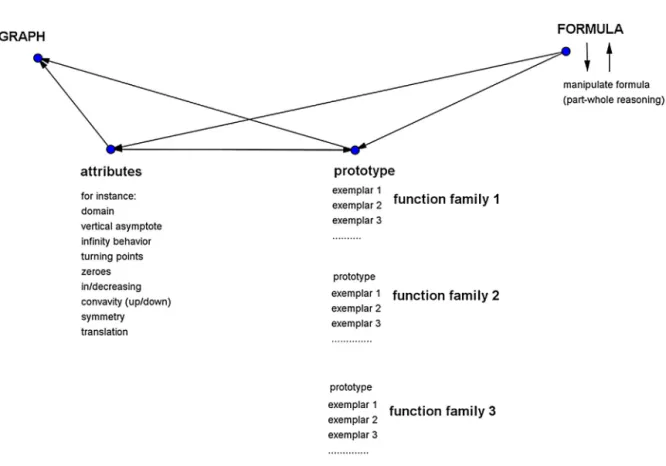
2.2. RecognitiondescribedusingBarsalou’smodelwithprototype,attribute,andpart-wholereasoning

Barsalou(1992)showedhowhumanknowledgeisorganizedincategoriesorconcepts.Peopleconstructthesecategories

basedonattributes.Whenataskrequiresadistinctiontobedrawnbetweenexemplarsofacategory,peopleconstructnew attributesandinthiswaynewcategories(Barsalou,1992).Forinstance,fortheconceptbird,attributes(variables)likesize, color,andbeak,withseveralvalues,canbeusedtodistinguishdifferentexemplars.Categoriescanhavealargediversityof exemplars,buthaveagradedstructure(Eysenck&Keane,2000;Barsalou,2008).Someexemplarsinacategoryaremore centraltothatcategorythanothers;thesearecalledprototypes.Forinstance,arobinisconsideredamoretypicalexample ofabirdthan,forinstance,achickenorapenguin.Whendealingwithexemplarsofacategory,peopletendtoassociate prototypicalfeatureswiththeseexemplars(Barsalou,2008;Schwarz&Hershkowitz,1999).Thetendencytoreasonfrom prototypescanposeproblems.Sinceconceptformationisnotnecessarilydoneusingpuredefinitions,WatsonandMason

(2005)emphasizedtheneedtogobeyondprototypesandtosearchfortheboundariesofaconcept.Inthiswayonebecomes

awareofthedimensionsofpossiblevariationandineachdimensionoftherangeofpermissiblechange(Billsetal.,2006;

Sandefur,Mason,Stylianides,&Watson,2013;Watson&Mason,2005).Thepersonalexamplespace,thecollectionof

examplesandtheinterconnectionbetweentheexamplesapersonhasathis/herdisposal(theaccessibleexamplespace), playamajorroleinhowapersonmakessenseofthetaskshe/sheisconfrontedwith(Watson&Mason,2005;Goldenberg

&Mason,2008).VinnerandDreyfus(1989)usedconceptimagetoemphasizethepersonalcharacterofpeople’smental

theexemplar(s)withthesetofhighestfrequencyofattributevaluesinthecategoryorwiththehighestcorrelationwith otherexemplarsinthecategory(Barsalou,1992).Prototypesaretheexamplesthatareacquiredfirstandareusuallythe examplesthathavethelongestlistofattributes:thecriticalattributesofthecategoryandtheself-attributes(non-critical attributes)oftheexemplar(Schwarz&Hershkowitz,1999).Prototypesareusedasareferencepointforjudgingmembership ofthecategory:anexemplarisjudgedtobeamemberofacategoryifthereisagoodmatchbetweenitsattributesandthose ofthecategoryprototype(Barsalou,2008;Eysenck&Keane,2000).Whenaskedforaprototypeofacategory,itisexpected thatapersonwillnotuseadefinitionofprototypebutwilluseageneralideaaboutwhatprototypesare:namely,the mostcentralexemplar(s)ofacategoryfromhis/herpersonalperspective.Asaconsequence,whendealingwithacategory,

theprototypesarethefirstexamplesthatcometoone’smindandarethenaturalexamplesthatareusedwithoutany

explanation.Examplesinthedomainofgraphingformulasincludeprototypicalformulaslikey=x2_andy=x3_,withtheir

prototypicalgraphs.Inthisstudyweusedthetermprototypereasoninginthisway.

Attributeunderstandingcanbedefinedastheabilitytorecognizetheattributesofafunctionacrossrepresentations

(Schwarz&Hershkowitz,1999).Forinstance,fromtheformulay=(x−1)(x−5),itisconcludedthatitsgraphisaparabola,

ithaszeroesatx=1andatx=5andasymmetryaxisatx=3.Theseattributesorpropertiesofthisfunctioncanberecognized inthegraphical,tabular,andalgebraicrepresentations.

Inhisproperty-orientedviewoffunctions,Slavit(1997)usedproperties(orattributes)likesymmetry,monotonicity, horizontalandslantasymptotes,intercepts(zeroes),extrema,andpointsofinflection.

Dependingonthetask,peopleconstructattributestobeabletodistinguishexemplars:inthisstudy,formulasandgraphs

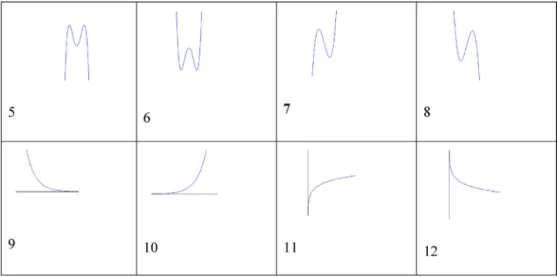
(Barsalou,1992).Todistinguishdifferentgraphsof4thdegreepolynomialfunctionsinFig.1,onecanuseattributeslike

symmetry,infinitybehavior,numberofturningpoints,numberofzeroes,andlocationofzeroesrelativetothey-axis.When relatingformulasandgraphs,asingraphingformulas,onechoosesorcreatesattributestofocusonfeaturesofformulasand graphs.Wecallthisreasoningaboutattributesandtheirvaluesattributereasoning.

Part-wholereasoningreferstotheabilitytorecognizethatdifferentformulasordifferentgraphsrelatetothesameentity: inthiscase,tothesamefunction.Inthegraphicalrepresentation,differentscalingcanresultindifferentpicturesofgraphs belongingtothesamefunction.Inthealgebraicrepresentation,formulamanipulationcanresultindifferentformulasofthe samefunction:forinstance,y=x2_{−4x,y=(x−2)}2_{−4,andy=x(x−4).Fromthesedifferentformulasdifferentattributesof}

thegraphcanberead.Therefore,part-wholereasoningisimportantintherecognitionofIGFs.

Forattributereasoningandpart-wholereasoningonehastograspthestructureofaformula.Intheliteraturethisiscalled symbolsense(Arcavi,1994).Symbolsenseisaverygeneralnotionof“whenandhow”tousesymbolsandhasseveralaspects, suchastheabilitytoreadthroughalgebraicexpressions,toseetheexpressionasawholeratherthanaconcatenationof letters,andtorecognizeitsglobalcharacteristics(Arcavi,1994).PierceandStacey(2001)usedalgebraicinsighttocapture thesymbolsenseintransformationalactivitiesinthe“solving”phaseofproblemsolving(PierceandStacey,2001).The algebraicinsightisdividedintwoparts:algebraicexpectationandtheabilitytolinkrepresentations.Algebraicexpectation hastodowithrecognitionandidentificationofobjects,forms,keyfeatures,dominantterms,andmeaningsofsymbols

(Kenney,2008;Pierce&Stacey,2001).Algebraicinsightisshownwhenapersonhasexpectationsaboutgraphsthatare

linkedtofeaturesofthesymbolicrepresentationandwhenequivalentalgebraicexpressionsarerecognized(Ball,Stacey,&

Pierce,2003;PierceandStacey,2001,2004).

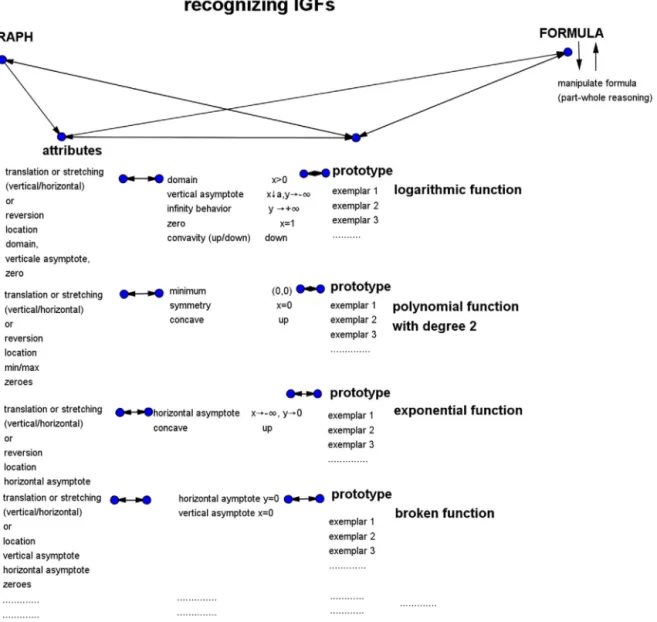
Thethreeaspectsprototype,attribute,andpart-wholereasoningfromSchwarzandHershkowitzcanbeusedtodescribe therecognitionprocessingraphingformulas.ABarsaloumodelforrecognizingIGFsisformulatedinFig.2.Inthecase ofgraphingformulas,itisdifficulttomentionallpossiblevalues.Forinstance,theattribute“zeroes”canhavevalueslike 0,1,2,3,toindicatethenumberofzeroes,butalsothelocationcanbeusedasvaluesofanattribute(forinstance,azeroat

x=5).Forthesakeofreadability,thevaluesbelongingtotheattributesareomittedinFig.2.

Fig.2. IGFsintheformofaBarsaloumodelbasedonSchwarzandHershkowitz(1999).

prototypeofafunctionfamily.Itisthenpossiblethatthegraphisdirectlyknown,orthat,usingattributereasoning,agraph canbevisualized.

Someexamplescanillustratethisrecognitionprocess.InIGFy=4·3x_{+2theprototype3}x_{canberecognized(prototype}

reasoning),andviaatranslation(attributereasoning)thegraphcanbevisualized.InIGFy=−2x(x−3)(x−6),theprototype

x3_{canberecognized,−x}3_{asareversion(attributereasoning),andviazeroesatx=0,x=3,x=6(attributereasoning)the}

graphcanbevisualized.However,wheny=−2x(x−3)(x−6)isnotrecognizedasamemberofafunctionfamilyorprototype ofafunctionfamily,theformulaisnotanIGF(Kopetal.,2015).Inthiscasethegraphhastobeconstructedby,forinstance, reasoningaboutattributeslikeinfinitybehaviorandzeroes.If,whengraphingy=4x−2_{,theformulacanberewrittento} y=4/x2_{(part-wholereasoning)andrecognizedasa1/x}2_{(prototypereasoning),theformulaisanIGF.Butwhenfromthe}

formulay=4/x2_{itisreadthatithasaverticalasymptoteatx=0,andthatalloutcomesarepositiveandwhenx→±∞then} y=0(infinitybehavior),thenwesaythatthegraphisconstructedthroughqualitativereasoning(Kopetal.,2015),andso theformulaisnotanIGF.

2.3. Globalandlocalperspectives

Covariationalreasoningisessentialforgraphingformulas.Incovariationalreasoning,oneisabletoimaginerunning throughallinput-outputpairssimultaneouslyandsotoreasonabouthowafunctionisactingonanentireintervalofinput values(Carlsonetal.,2002).InrecognizingIGFsonehastohaveapictureofthefunctionasanentity.Intheliteraturethis perspectiveofthefunction,seeingthefunctionasawhole,isalsoaddressedastheobjectorglobalperspective(Confrey

&Smith,1995;Even,1998;Gray&Tall,1994;Oehrtmanetal.,2008;Sfard,1991).Thereisalsoanotherperspectiveofthe

function,namely,toseeafunctionasaninput-outputmachine.Thisperspectivehastodowiththefundamentalviewon functions(whatitmeansthatacertainy-valuebelongstoagivenx-value),andisaddressedasthepointwise,process, orcorrespondenceperspective.Switchingbetweenbothkindsofperspectiveisnecessaryforreasoningaboutfunctions.

Slavit(1997)spokeaboutthelocalandglobalnatureoffunctionalgrowthpropertiesinaddressingbothkindsofperspective

(Slavit,1997).Theglobalgrowthpropertiesconcernattributeslikesymmetry,monotonicity,horizontalandslantasymptotes,

Fig.3.Anumberofthecardsusedintask1.

usingthesepropertiesorattributes.Beforethecurrentresearch,itwasunknownwhichattributesexpertsuseinrecognizing IGFs.

2.4. Researchquestions

Inthecurrentstudywefocusedonexperts’repertoiresofformulasthatcanbeinstantlyvisualizedusingagraph(IGFs) andontheirconceptimagesofIGFs,withattributes,prototypes,andpart-wholereasoning.Weexpectedthatexpertswould havelargerepertoiresofIGFsthatarestructuredincategories.However,wedidnotyetknowwhatanexpertrepertoireof IGFswouldbe.

Weexpectedexpertstobeabletomanipulatealgebraicformulas(part-wholereasoning),tousesymbolsenseandin particularalgebraicinsight,andtousesetsofattributeswithvaluesetstodistinguishdifferentgraphs.However,wedidnot knowwhichprototype,attribute,andpart-wholereasoningtheywoulduseinlinkingformulasandgraphsofIGFs.

Thisleadtothefollowingresearchquestions:

Canwedescribeexperts’repertoiresofinstantgraphableformulas(IGFs)usingcategoriesoffunctionfamilies? WhatdoexpertsattendtowhenlinkingformulasandgraphsofIGFs,describedintermsofprototype,attribute,and

part-wholereasoning?

3. Method

Thecurrentstudycanbecharacterizedasanexploratorystudy,inwhichweinvestigated“snapshots”ofexperts’concept imagesoffunctionfamilieswiththeiralgebraicformulasandgraphs.

3.1. Tasks

Threedifferenttasksweredevelopedtoelicittheexperts’repertoiresofIGFsandtoexploretheexperts’prototype, attribute,andpart-wholereasoning:acard-sortingtask,amatchingtask,andamultiplechoicetask.

Card-sortingtasksareoftenusedinelicitingstructuredknowledge(Chietal.,1981;Jonassen,Beissner,&Yacci,1993;de

Jong&Ferguson-Hessler,1986;Goldenberg&Mason,2008;Sandefuretal.,2013).

Intask1,60formulasweregivenandtheparticipantswereaskedtocategorizethemaccordingtotheirgraph.After this,theywereaskedtogiveanameandaprototypicalformulaforeachoftheircategories.Westructuredthistaskby addinggraphstothecardsshowingtheformulas.Whensuchtasksaregivenwithoutstructuringbeforehand,gettinga completepictureorcomparingtheresultscanposeproblems,becauseofthedifferentcriteriathatcanbeusedtosortthe cards(Ruiz-Primo&Shavelson,1996).Becauseweaddfourgraphstothe60cardswithformulas,theparticipantswere explicitlycompelledtofocusonthegraphsoftheformulas.Wedidnotindicatewhetheraparticipantshoulddiscriminate betweenparabolaswithamaximumorminimumbecausethelevelofdetailcanbeanindicatorofexpertise.Fig.3shows 20cardsfromtask1.Mostoftheseformulas,butnotall,arerelatedtooneofthebasicfunctionfamilies,whicharestudied ingrades10–12:y=xn_,y=ax_,y=log

2(x),y=1/x,y=√x,y=ln(x),y=ex.Since,weusedthebasicfunctionsfromsecondary

Fig.4.Somealternativesoftask2.

InTask2,thematchingtask,alistof40formulaswasgivenandtheparticipantswereaskedtoselectthecorrectalternative outof21alternatives:20graphsandonealternativestating“noneofthese”.Thislastalternativewasprovidedtodiscourage guessing.Inthistaskthefocuswasoninstantlinkingofformulastotheglobalshapeofgraphs.Thereforeastricttime limitwasusedtoencouragerecognitionandtodiscourageconstructionofagraph.Wechoseamatchingtaskwithmany alternativesratherthanagraphingtasktoindicatethelevelofdetailthatwasneeded:theexpertshadtorecognizethe globalshapeofthegraphofthegivenformula.

The formulas used in this task resembled the formulas used in the first task. The following are some

exam-ples:y=2x(x−2)(x+4);y=6x2_−2x4_{; y=e}2x_{+1;y=x−4/x; y=4−2x+x/4; y=4/2}x_{; y=}√_{x−6+2;y=ln(e}2_{·x); y=2x}−4_; y=2(x−1)4_−4;y=

Task2wasalsodevelopedtoelicitparticipants’repertoiresofIGFs.Thereforesomefunctionswereaddedthatdonot belongtothefunctionfamiliesofbasicfunctions,forinstance,y=

toinvestigatetheboundariesoftheexperts’repertoiresofIGFs.Becausetheformulasusedweresimilartothoseintask1, thistaskwasusedtovalidatetheresultsoftask1.When,forinstance,intask1nodistinctionwasmadebetweenincreasing anddecreasingparabola,butintask2thisdistinctionwasmade,itwasconcludedthattheparticipantcouldindeedmake suchadistinction.

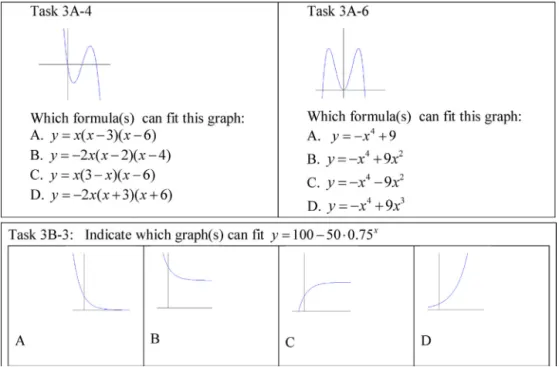
Tasks3Aand3B,thinkingaloudmultiplechoicetasks,weredevelopedtoelicittheparticipants’prototype,attribute,and part-wholereasoningandinthiswaytogetmoredetailedknowledgeoftheparticipants’conceptimages.Theparticipants wereaskedtochoosethecorrectalternativeoutoffouralternatives.AsimilartaskwasusedbySchwarzandHershkowitz

(1999)intheirstudyofconceptimagesoffunctions.Bothtasksconsistedofsixitems.Intask3Baformulawasgivenandthe

expertshadtofindthecorrectgraph.Intask3Aagraphwasgivenandtheexpertshadtoprovideaformula.Ingeneral,tasks like3Aareconsideredtobemorechallenging.Butthisisnotclearwhendealingwiththefunctionfamiliesofwell-known basicfunctions.Inthiswaywegotmoredetailedinformationabouttheexperts’conceptimagesofIGFs.Threeexamplesof thistaskareshowninFig.5.

Theformulaswereagainchosenfromthesamesetoffunctionsasintasks1and2.Participantshadtoconsiderall alternativesbecausemorethanonealternativecouldbecorrect.

Intasks1and2thefocuswasonsketchesofgraphs;inthistask,moredetailedanswerswereneeded.Forinstance,in tasks1and2itwasnotnecessarytodistinguishy=−2x(x−2)(x−4)andy=−2x(x+3)(x+6),butintask3thisdistinction hadtobemade(seetask3A-4inFig.5).

3.2. Participants

Fig.5.Someexamplesoftask3:task3A-4,3A-6,3B-3.

3.3. Dataanddataanalysis

3.3.1. Datacollectionprocedure

Writteninstructionswerehandedoutforeverytask,togetherwithanindicationofthetimeneededtoperformthetask. Fortask1,atimeindicationofmaximum40minwasgiven;fortasks2and3,20min.Foralltasks,thetimeneededwas recorded,asthetimerequiredtoperformataskcanbeanindicationofexpertise.Duringthetasksthefirstauthoronly emphasizedtheneedtokeeponthinkingaloudwhentheexpertsstoppedtalking.Aftereachtask,thefirstauthoraskedthe expertstolookbackandtodescribethestrategies,theyhadusedinthetask.Theinterviewswerevideotaped.

Intask1,thecard-sortingtask,60cardswerelaidonatableandtheparticipantscouldphysicallygrouptheformulas intodifferentcategories.Afterwards,thecategoriesweregluedonalargesheet.Theparticipantsthenwrotethecategory namesandtheprototypicalformulasforeachcategory.Intask2andtask3,theparticipantsfilledintheanswersonaform. Duringtasks1and3theparticipantswereaskedtothinkaloud;thiswasvideotaped.Thinkingaloudisconsideredto givereliableinformationabouttheproblem-solvingactivitieswithoutdisturbingthethinkingprocess(Ericsson,2006).For task3thethinking-aloudprotocolsweretranscribedinordertoanalyzetheprototype,attribute,andpart-wholereasoning.

3.3.2. Dataanalysis

3.3.2.1. Task1.Theaimoftask1wastogatherinformationonwhichcategoriesexpertsuseintheirrepertoiresofIGFs.It wasexpectedthatexpertswouldusesalient,globalpropertiesofgraphs,likesymmetry,in/decreasing,verticalasymptotes, infinitybehavior,andnumberofturningpoints,tocategorizetheirIGFs.Basedonthesesalientproperties,thefirstauthor madeatheoretical,hypotheticalexperts’categorizationbeforethestartofthisstudy.Thecategorizationsofthefiveexperts werecomparedwitheachotherandwiththefirstauthor’scategorization.Basedonthesefindingsacommoncategorization wasconstructed.Thiswasdoneinseveralsteps.First,commonelementsinthecategoriesandprototypesintheexperts’ categorizationsandthefirstauthor’scategorizationweredetermined.Fromthesefindingsapreliminarycommonexpert categorizationwasformulated.Inthesecondstep,thelevelofdetailwasconsidered.Ahigherlevelofdetailmeantthat subcategorieswereused.Ifoneormoreexpertsusedahigherlevelofdetail,thenthislevelofdetailwasusedinthe(final) commonexpertcategorization.Inthelaststep,thedistancesbetweenindividualcategorizationsandthecommonexpert

categorizationwerecalculated.Weconsideredwhethersmalladjustmentsinthecommonexpertcategorizationwould

resultinalowerminimumofthetotalofalldistances.Whennoprogressioncouldbemade,thefinalcommonexpert

categorizationwasfound.

Todeterminethedistancebetweenanindividualcategorizationandacommoncategorization,thefollowingprotocol

wasused:

-Ifnosubcategoriesweremadeintheindividualcategorizationandthecommonexpertcategorizationmadeadistinction betweenincreasinganddecreasing,thenthedistanceincreasedby+2(forinstance,nosubcategoriesbetweenparabolas withmaximumandparabolaswithminimumgaveanincreaseofthedistanceby+2ifthecommonexpertcategorization madethisdistinction)

-Iftwocategoriesofthecommonexpertcategorizationweremergedintheindividualcategorization(otherthanthe distinctionbetweenincreasinganddecreasing),thenthedistanceincreasedby+4(forinstance,3rdand4thgradefunctions wereputtogetherinonecategory)

-Ifa completely newcategory, differentfromthecommon expertcategorization, wasformulated,then thedistance

increasedby+6.

3.3.2.2. Task2.Inthistaskthenumbersofmistakesperexpertwerecounted.Themistakeswereindicatedinatablein ordertoseewhethertheyweremadeinparticularfunctionfamilies.

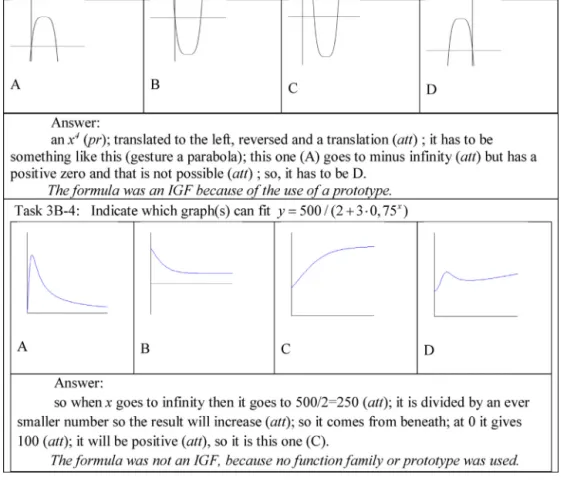
3.3.2.3. Task3.Toanalyzetheresultsoftask3,thetranscriptswerecutintofragmentswhichcontainedcrucialstepsof explanations:ideaunits.Ideaunitsareprimitiveelementsinthejustificationsofparticipants(Schwarz&Hershkowitz, 1999).TheseideaunitswereencodedusingtheelementsfromFig.2:prototype,attribute,orpart-wholereasoning.

Sinceprototypesarethenaturalexamplesofcategoriesthatcanbeusedwithoutanyexplanation,graphsandformulas thataparticipantusedasthestartofareasoningprocesswereconsideredprototypesfortheexpert.Ifnoprototypereasoning wasusedorfunctionfamilywasmentioned,wesaidthattheformulawasnotanIGF,andthatthegraphwasconstructed.

Thefragmentsoftheprotocolswereencodedasfollows:

-pr(prototypereasoning):onlyaprototypicalexemplarwasmentioned;forinstance,“itlookslikealog”,“itisanxinthe power6”,“itisanexpo”,“itisanoscillation”.Ifafunctionfamilywasmentioned,likein“itisanexponentialfunction”or “4thdegreepolynomial”,thiswasconsideredprototypereasoning

-att(attributereasoning):anattributewasmentioned;forinstance,“thisonehasaverticalasymptoteatx=0”,“itisalways positive”,“itgoestominusinfinity”.

-pw(part-wholereasoning):theformulawasmanipulatedtoanequivalentformula,forinstance,y=4x−2toy=4/x2

-con(construction):nofunctionfamilyorprototypewasmentioned,theformulawasnotanIGF:thegraphwasconstructed through,forinstance,attributereasoningorcalculatingpoints.

WegivetwoexamplesoftheencodinginFig.6.

4. Results

4.1. Resultsoftask1

Theexperts’andauthors’categorizationsareshowninAppendixA.Theexpertsshowedagreatdealofagreementintheir choicesofcategories,namesofthesecategories,andprototypesofthecategories.OnlyexpertSusedadifferentapproachin hiscategorizationofpolynomialfunctions.Hebasedhiscategorizationonthenumberofturningpoints.Theotherexperts allusedthedegreeofpolynomialfunctions.The4thdegreepolynomialfunctionsweredividedintographswithaW-form, aM-form,andaV-form(orastheexpertsmentioned,“increasingordecreasing”).Nolargedifferenceswerefoundon exponentialfunctionsandlogarithmicfunctions,althoughsomeexperts(PandR)madenodistinctionbetween“normal” and“reversed”graphs(forinstance,y=ex_versusy=e−x_{andy=ln(x)versusy=−ln(x)).Allexpertsagreedonlinearbroken} functionsandsquare-rootfunctions.Moredifferenceswerefoundinthecategoriesofpowerfunctions,whereonlyexpert Qmadedistinctionsbasedondomainand/oronconcavity.

Intheconstructionofthecommonexpertcategorization,thedistancesbetweenindividualcategorizationsandthe commonexpertcategorizationwerecalculated.ThefinalcommonexpertcategorizationisshowninTable1.

Thefollowingdistancesfromthefinalcategorizationwerefound:11,3,19,20,and15(forP,Q,R,S,andT,respectively). Theexpertsneededanaverageof18min:23,20,11,14,and21min(forP,Q,R,S,andT,respectively).

Forthistasktheexpertsusedalotofpart-wholereasoninginordertocategorize,forinstance,thefollowingformulas

correctly:ln(e2x_{),(1−x)(2+x)+x}2_{,ln(1/x),x(x−1)/(x+1)(x−1),(2x}1₃₎ 5

.

Fig.6.Examplesoftheencodingoffragmentsofprotocolsoftask3.

Table1

Commonexpertcategorization.

Categories:

Linear

x+5(4−x),ln(e2x_{),(1−x)(2+x)+x}2 Parabola

parabolawithmax:x(9−x),−(x−3)2_{+2,(x+5)(3−x),2x−3(x+2)(x−2),−(x−1)}2_+2(x−1)+6; parabolawithmin:x2_{−7(x−5),(6−x)}2_,x2_+(−x+1)2

3rddegreeoscillation

(x2_{−7)(x−5),2(x−3)}2_(x+3),2x3_+4x2_−16x,x3_−9x,e3ln(x) 4thdegree

W-shape:x4_−16x2_+28,(x2₋₇₎2

;(6e_{degreeW-shape:3(x}4_−6)(x2_−8)); M-shape:−3(x2_−4)(x2_−6),2x3_{(6−x);V-shape:(x+3)}4_−9,x2_(9+x2₎ Exponential

increasing:4−3+x_,2.(√₂₎x_{;decreasing:18·0.3}x_,26−x_,8e−x_,10−2x+5_,8/3x_;

reversedexponential:6−2x_;100−ex

Logarithmic

inceasing:ln(e2_·x),1+2_{log(x),ln(x)+ln(2);decreasing:−ln(x),ln(1/x)} distractor:1/ln(x)

Hyperbola

hyperbola:x(x−1)/(x+1)(x−1),(4x+2)/x,1−5/(x+1)

powerfunctionswithnegativeoddpower:8x−3_{;withnegativeevenpower:2/x}4_,3x−2 slantasymptote:x−4/x;twoverticalasymptotes(x2₋₁₎−1

,2/x−3/(x−1) ‘Roots’

increasing‘√x-like’:3√x+6,2√x−6;(100x)12_{;decreasing‘}√_x-like’:4√_{10−x,(2−x)}12₊₂

halfacircle:

exponent‘1

3-like’<1:2

3

√

x,8√3x4_{/2x;exponent‘}1

3-like’>1:(2x 1 3)

5

;exponent‘11 2-like’:2x

Table2

Resultsoftask2.

Participant Numbermistakes Mistakes

P 3 (4x+1)/(x+2);7x√x;10/x3

Q 1 (4x+1)/(x+2)

R 1 (4x+1)/(x+2)

S 0

T 5 6x2_−2x4_;2x−4_{;4−2x+x/4;(4x+1)/(x+2);5x}7

Table3

Timeneededfortask3Aand3B,thetotalnumberofmistakes,andthenumberofIGFsandconstructions.

Participants Time3A Time3B Numberofmistakes NumberofIGFs Numberofconstructions

P 4:54min 7:44min 0 10 2

Q 4:16min 2:13min 0 11 1

R 3:56min 6:27min 0 9 3

S 4:02min 2:44min 0 6 6

T 6:16min 2:46min 0 9 3

detailedcategorizationwouldbepossible,butnotwithoutcalculations:“InthenextstepIwouldhavetomakecalculations;

Iwouldnottrustmyselftosaymoreaboutthiscategorizationoffthetopofmyhead”(expertQ).

4.2. Resultsoftask2

Theresultsoftask2(seeTable2)showedthatthreeoutofthefiveexpertsmadenomistakesoronlyonemistake.Most

mistakesweremadewiththeformulay=(4x+1)/(x+2).Fourofourexpertsselectedthealternativewiththeincreasing hyperbola.Fromtheotheralternativesitcouldhavebeenconcludedthatadistinctionhadtobemadebetweenanincreasing andadecreasinghyperbola.Sinceastricttimelimitofonly30sforoneformulawasusedandallexpertsfinishedthistask easilywithinthistimelimit,itwasconcludedthatalltheformulasthatdidnotbelongtothealternative“noneofthese” couldbeconsideredIGFsfortheexperts.

Fromtheobservationsandinterviewswelearnedthatallexpertsfirstexaminedthe20graphalternativesandhada globalviewoftheformulastogetanimpressionofwhichaspectswouldplayaroleinthistaskandwhattheyhadtofocus on.Allexpertsreadalmostallgraphsbymentioningafunctionfamilythatfittedthegraph.Whenperformingthistask,they usedpart-wholereasoningifnecessary,recognizedafunctionfamilyandusedattributereasoningtodiscriminatebetween differentoptionsofthesamefunctionfamily.Forinstance,y=4x_−5y=3e−0,5x+4_−4,y=4/2x_{wereallrecognizedasmembers}

oftheexponentialfunctionfamily,attributereasoning,likeinfinitybehaviorandreversingaprototypicalgraphwasused tochoosethecorrectalternative.

4.3. Resultsoftask3

Intask3theprotocolswereanalyzedusingprototype,attribute,andpart-wholereasoning.Fromtheencodedprotocols, wefoundthatexpertsoftenstartedwithprototypesoffunctionfamilies,followedbyattributereasoning.

Wegivefourexamples(pr=prototype;att=attributereasoning;pw=part-wholereasoning):

Example1(:expertQintask3A-4(3rddegreepolynomialinFig.5)). Somethingwithahigherdegree(pr),decreasing(att), let’ssee;thisissomethingthatincreases(att),zeroesindeedat0,2,and4(att),thatlooksreliable;andthisat0,3,and6, andthatwillbepossible(att);andthisoneincreases,oh,noitdecreasestoo(att);wouldbeapossiblealternative;andthis onenot,ithasitszeroesonthewrongside(att).

Example2(:expertQintask3A-6(4thdegreepolynomialinFig.5)). Let’ssee,4thdegree(pr),downwards(att);A.thisone hasnooscillations,andisonlytranslated(att);B.ispossible,wherearethezeroes?,factorizinggivesme−x2_+9(pw),so

zeroesatx=3andx=−3(att);C.isnotpossible,becausewhenIdividedbyx2_{(pw)thennoextrazeroes;d.whenIdivided}

byx3_{(pw),itgavemeonlyonemorezero;soithastobeB}

Example3(:expertSintask3B-3(exponentialfunctioninFig.5)). 100−50·0.75x_{isanexponential;function(pr)withy=100}

asahorizontalasymptote(att);thatleavesB.andC.;itis100minus....,soitcomesfrombeneaththeasymptote(att),soit hastobeC.

Example4(:expertTintask3B-2(Indicatewhichgraph(s)canfity=−x(x−2)(x−4))). Thisisapolynomialfunctionofdegree 3(pr)andthosegraphsalllookofdegree3(pr);itis−x3_{(att),sothatmeansthesealternativesarenotpossible(indicatedA.}

andB.);thesetwoarepossiblebutitisonlythisone(C.)becauseD.hasnotthecorrectzeroes(att).

ofapolynomialfunctionofdegree3respectivelydegree4.InFig.7itisindicatedwhichexpertsstartedintask3Atheir thinkingaloudwithmentioningaprototypeofafunctionfamily.Theotherexpertsworkedfromthealternativeformulas tothegraph.

Fromtheprotocolsweseethattheyexpertsusedprototypicalformulasandprototypicalgraphsofbasicfunctions. Theyusedprototypesofexponential,logarithmic,even,andpolynomialofdegree2,3and4functions.Also,y=

(half acircle)wasconsidereda functionfamily.OnlyexpertQusedy=1/x2 _{asafunctionfamily. Attributesthat were}

usedtodiscriminatebetweendifferentalternativeswere:increasing/decreasingofgraphlinkedtopositive/negativehead coefficient,infinitybehaviorandhorizontalasymptote,translations,verticalasymptote,numberofzeroesandlocationof zeroes,reversingagraph,positive/negativeoutcomes,domain,andpointofinflection.

ExpertSseemedtousealotofconstructions,perhapsbecauseaprototypeorfunctionfamilywasnotmentioned.From theprotocolsandresultsoftheothertasksitwasconcludedthatthesefunctionfamilieswereimplicitlyusedbythisexpert. Fromobservationsandinterviewswelearntthattheexpertsthoughtthefunctionsusedintask3Awere“easier”than thoseusedintask3Bbecausetheyonlyrequiredsimpletransformations.Anotherreasonforthedifferencesbetweentask 3Aand3Bwastheamountofvisualinformationintask3B:“fourformulasandonegraphiseasiertodealwiththanfour graphsandoneformula”(expertQ).ExpertPmentionedthatingeneral“itismoredifficulttothinkfromthegraphthan tothinktothegraph”.Nevertheless,allexpertsindicatedthatbothtasksrequiredthesameknowledgeelements:namely, linkingvisualfeaturesofthegraphsandfeaturesoftheformulas.

5. Conclusionsanddiscussion

5.1. Conclusions

Thefirstaimofthecurrentresearchwastodescribeexperts’repertoiresofIGFs.Wehypothesizedthatexpertswould usecategoriestoorganizetheirknowledgeofgraphsandformulas.Theexperts’resultsintask1showedthatthecategories theyconstructedwereverysimilarandalsothatthecategorydescriptionsweresimilar.Thesedescriptionswereclosely relatedtothefunctionfamiliesofbasicfunctionsthataretaughtinsecondaryschool:linearfunctions,polynomialfunctions, exponentialandlogarithmicfunctions,brokenfunctions,andpowerfunctions.OnlyexpertSuseddescriptionscontaining numbersofturningpointsforthepolynomialfunctions.Thereforeacommoncategorizationcouldbeconstructed.The dis-tancesbetweentheindividualcategorizationsandthefinalcategorizationvariedfrom3to20.Manyofthesedifferences couldbeexplainedbytheabsenceofsubcategories.Forinstance,someoftheexpertsdidnotdistinguishbetween

increas-inganddecreasingexponentialgraphsorbetweenparabolawithamaximumorwithaminimum.However,theexperts’

performancesintask2confirmedthattheycouldrecognizethesedifferencesbetweensubcategoriesastheymadealmost nomistakesinthistask.

Thetimetheexpertsneededtoperformthiscategorizationtaskvariedfrom11to23min.Whentakingabout20min tocategorize60cards,theexpertsneededonly20spercardtoread,torecognize,tocomparewithothers,andtogroup

formulaswithsimilargraphs.Thismeantthattherewasalmostnotimefortheconstructionofnew,unknowngraphs.

Someoftheformulas,likey=1/ln(x),y=(x2₋₁₎−1_{,y=x−4/x,y=2/x−3/(x−1)werecategorizedinacategorywithasingle}

ThesecondaimofthecurrentstudywastodescribewhatexpertsattendtowhenlinkingformulastographsofIGFs.The recognitionprocesswhenworkingfromformulastographscanbewelldescribedusingtheBarsaloumodelofFig.2.Itis showninTable3thatinrecognizingIGFs,theexpertsoftenstartedwithprototypes.Thisprototypereasoningwas,when necessary,followedbyattributereasoning.Forinstance,y=−2x(x−3)(x−6)isrecognizedasaprototypical“x3_”,whichis

“reversed”andhaszeroesat0,3,and6;y=log2(x+3)asalogtranslatedtotheleft;y=−(x+2)4+16asan“x4”,reversedand

translated;y=

whofoundthatproficientstudentsusedprototypesasleversforhandlingotherexamplesandshowedgreaterunderstanding of(critical)attributes.

Theexpertsalsorecognizedprototypicalgraphsforwell-knownfunctionfamilies,astheyshowedintask2andtask3A. Forwell-knownfunctionfamiliesthereseemedtobelittledifferencebetweenworkingfromformulatographandworking fromgraphtoformula.WhenworkingwithIGFs,theexperts’conceptimagesthatweretriggeredbythegivenformulaor givengraph,seemedtocontainequivalentformula(s),graph(s),attributesofgraphsandofformulas,functionfamilywith prototypes,formulasofotherfunctionsinthisfunctionfamily.

Inordertoelicitexperts’attributereasoning,allattributestheexpertsusedintask3weregathered:translationtothe right/leftandabove/below,stretchinghorizontalorvertical,reversion(oftenindicatedbyreasoningaboutnegativehead coefficient),infinitybehavior(withhorizontalasymptotes),increasing/decreasing,numberandlocationofturningpoints, locationandnumberofzeroes,positive/negative,domain,pointofinflection,andverticalasymptotes.

Particularattributesseemedtobelinkedtoparticularfunctionfamilies.Asshownintask3,theseconnectionscould workbothways:fromfunctionfamiliestosalientattributesofgraphsandfromgraphswithsalientattributestofunction families.Thesesalientattributesofafunctionfamilyarecharacteristicofthemembersandprototypesofthefunctionfamily. Forinstance,averticalasymptotewasdirectlylinkedtologarithmicfunctionsorbrokenfunctions.And,whenconfronted withpowerfunctionswithn=p/q,someinstantlystartedwithafocusondomainandconcavity.Forthedifferentfunction familiesinourresearch,theexpertsusedsalientattributes:limiteddomainwaslinkedtorootfunctions,powerfunctionsand logarithmicfunctions;verticalasymptoteswerelinkedtologarithmicfunctionsandbrokenfunctions;horizontalasymptotes werelinkedtoexponentialfunctionsandbrokenfunctions;symmetrywaslinkedtoevenpolynomialfunctions.

Expertsusedattributesappropriatetothetasks.Forinstance,whentheyhadtolinkformulastoglobalgraphs(tasks1 and2),theypaidnoattentiontothefactor7iny=7x√x,ortothefactor3andterm1iny=4−x+3_{+1.Butwhenparameters}

influencedtheglobalshapeofthegraph,theseparametersweregivenampleattention.Forinstance,theminussignsof theheadcoefficientiny=−x4_+9x2_andiny=2√_{8−xwhichreversedtheprototypicalgraphsweredirectlynoticedand}

mentioned.Whenmoredetailedgraphswererequested,asintask3,theexpertsagainonlyusedthoseattributesthatwere neededforthetask.Forinstance,theydidnotmentionanythingaboutthefactor0.1iny=0.1·x2_{orabouttheterm12inthe}

formulay=x6_{+12,becausethesewerepositivenumbers.Butwhenthetaskdemandedit,theexpertsquicklynoticedthe}

attributesandvaluesneededtographtheformulas.Forinstance,theexpertsinstantlyrecognizedthedifferentlocationsof thezeroesiny=x(3−x)(x−6)andy=−2x(x+3)(x+6).Thesefindingsshowthattheexpertsworkedefficientlyanddidnot payattentionto“whatisnormal”(Chietal.,1981;Chi,2011).

Theexpertssometimeshadtoshowtheirabilitiesinalgebraicmanipulation.Asexpected,theyhadnoproblemswiththis aspectofpart-wholereasoning:thiswasshownin,forinstance,y=6x−2(intask3B),andy=8x−3,y=x(x−1)/((x+1)(x−1)), andy=(1₋x)(2+x)+x2_(intask1).

Theseresultsshowthatexperts’processesof recognitionof IGFscanbedescribed usingthemodelin Fig.2:with prototypes,supportedbyattributeandpart-wholereasoning.

5.2. Discussionandimplications

5.2.1. ABarsaloumodelforrecognitionofIGFs

Thecurrentfindingshighlightthetwohighestlevelsofrecognitionoftheframeworkforstrategiesingraphingformulas (Kopetal.,2015).WedefinedformulasattheselevelsasIGFs,instantlygraphableformulas.Wedescribedtheexperts’ repertoiresofIGFsanddescribedwhatexpertsattendedtoinrecognizingIGFs.Weshowedthattheexpertsusedprototypes andattributereasoninginrecognizingIGFsandfoundhowparticularattributeandvaluesetswerelinkedtoparticular functionfamilies.Forinstance,givenalogarithmicformulasuchasy=log3(2x+4)−3,aprototypey=log3(x)ory=log(x)

wasinstantlyidentifiedandattributereasoning(translation,domainx>−2,and/orverticalasymptoteatx=−2)resultedin agraph.Wealsofoundthatforfunctionfamiliesofbasicfunctions,theexpertscouldeasilyworkfromgraphtoaformula. Givenagraph,theyinstantlyrecognizedafunctionfamilythatfittedthegraph.Forinstance,agraphwithattributeslike domainx>a,averticalasymptoteatx=aandconcavedownwasinstantlyidentifiedasalogarithmicfunction.Thisimplies thattheBarsaloumodelbasedonSchwarzandHershkowitzinFig.2canbeexpandedwithlinkagesbetweenattributeand valuesets,prototypesandfunctionfamiliesandwithlinkagesfromgraphtoattributes,prototypes,andfunctionfamilies.In

Fig.8. ABarsaloumodelbasedonSchwarzandHershkowitzwithfunctionfamiliesandtheirsalientattributes.

5.2.2. Globalpropertiesingraphingformulas

Theexpertsinourstudyfocusedonattributesandvaluesthatinfluencedtheglobalshapeofthegraph.Forinstance, aparameterthatreversedtheprototypicalgraphofy=x4_{wasgivenampleattention,like−2iny=−2x}4_{,butaparameter}

thatresultedinonlyasmallchangeoftheprototypicalgraphwasnotmentioned,suchas0.1iny=0.1x4_{.Intheirattribute}

reasoning,theexpertsfocusedonattributesandvaluesthatgaveagreatdealofinformationaboutthewholegraph.These attributescanbeconsideredtheglobalgrowthpropertiesofSlavit’sclassificationoffunctionproperties(Slavit,1997). Startingwiththeseglobalpropertiesisconsideredtobemoreefficientingraphingformulasthanusinglocalproperties

(Even,1998;Slavit,1997).

InthecurrentstudywefoundthattheexpertsusedasetofattributesandvaluesthatdifferfromSlavit’sglobalproperties, partlybecauseSlavit’sfocuswasmoreonthefunctionconcept,whereasourfocuswasontherelationbetweenformulaand graph.SeveralglobalpropertiesSlavitused,suchasintegrabilityandinvertibility,werenotmentionedatallbyourexperts. Basedonthecurrentresults,wesuggestthatrelevantglobalpropertiesforrecognizingIGFsmaybesymmetry,infinity behavior(includinghorizontalandslantasymptotes),verticalasymptotes,domain,increasing/decreasingonintervals,sign (reverse),andconcavity.Forlocalproperties,wesuggestzeroes,turningpoints,pointsofinflection,andindividualpoints.

5.2.3. Suggestionsforfurtherresearchandteaching

“areversed....”,“itgoestoinfinity”,“itgoesup”,“itcomesfrombelow”,“ininfinityitis...”,“thisoneisonlypositive”,“log totheright”,“anoscillationdownwards”,“a−x3_”.

Thesedescriptionsshowthattheexpertsoftendidnotusetheformalmathattribute/propertyconcepts,butusedboth picturesofthewholegraphandactionlanguagesuchas“it(thegraph)runs...”.Peopletalkubiquitouslyaboutabstract conceptsusingconcretemetaphors(Barsalou,2008).Metonymiesandmetaphorsarenecessaryforefficientcommunication andinthelearningofmathematicalconcepts(Presmeg,1998;Zandieh&Knapp,2006).Furtherresearchisnecessarytofind outhowtheseexperts’metonymiesandmetaphorscanbehelpfulintheefficientteachingofgraphingformulas.

ArepertoireofIGFsisnecessaryforgraphingformulas.EisenbergandDreyfus(1994)wroteabouttheneedforarepertoire ofbasicfunctionsandknowledgeofthecharacteristicsoftherepresentationsofthesefunctions.Slavit(1997)speaksabout “propertynoticing”,theabilitytorecognizeandanalyzefunctionsbyidentifyingthepresenceorabsenceoftheseproperties andtheneedfora“library”offunctionalproperties.Ourfindingsshowhowexpertsusedprototypeandattributereasoning forgraphingformulasandsogiveanimpressionofanexpert“library”ofproperties.Fig.8,aBarsaloumodelbasedonSchwarz andHershkowitz,showshowforIFGsthesefunctionfamilies,prototypes,attributes,andpart-wholereasoningareintegrated intheexperts’conceptimages.Ourfindingsmaybehelpfultofurtherdescribetherecognitionandidentificationofobjects, forms,keyfeatures,anddominanttermsusedinPierceandStacey’salgebraicinsight(PierceandStacey,2001;Kenney, 2008).NotonlyingraphingformulasbutalsowhenusingCASorgraphicalcalculatorsoneneedsthisalgebraicinsight.For instance,Heidetal.(2012)showedhowsolvingtheequationln(x)=5sin(x)requiredknowledgeofthecharacteristicsof functionfamiliesofbothformulasy=ln(x)andy=5sin(x)andtheabilitytolinkthegraphimagestotheformulas(Zbiek&

Heid,2011).

Theresultsofthisstudycanberelevantforteachingalgebraandinparticularfunctions.Studentscontinuetoexperience difficultieswithseeingtherelationshipbetweenalgebraicandgraphicalrepresentations,althoughgraphingtechnologycan supportstudents’understandinginlinkingrepresentationsoffunctions(Kieran,2006;Ruthven,Deaney,&Hennessy,2009). Inordertofurtherimproveeducation,wefirstneedadomain-specificknowledgebase(DeCorte,2010).Expertiseresearch canprovidesuchaknowledgebase(DeCorte,2010;Campitelli&Gobet,2010;Stylianou&Silver,2004).Thecurrentfindings showwhatknowledgeexpertsusedinrecognizingIGFs:theyusedthebasicfunctionstoorganizethefunctionfamilies,used prototypestohandleotherexemplarsoffunctionfamilies,andusedprototypesandattributestolinkgraphsandformulas offunctionfamilies.Insecondaryschoolcurriculamuch attentionispaidtobasicfunctions,inparticulartolinearand quadraticfunctions.Ourstudysuggeststhatonlylearningandpracticingbasicfunctionsisnotenoughtobecomeproficient inlinkingtheformulasandgraphsoffunctions.Studentsneedtoknowhowtohandleparametersinformulasandneed opportunitiestointegratetheirknowledgeofprototypesandattributesoffunctionfamiliesintowell-connectedhierarchical mentalnetworks.Besidessuchaknowledge-baseforrecognition,studentsneedheuristicmethods,likesplittingformulas andqualitativereasoning,whenrecognitionfallsshort(Kopetal.,2015).

Forgraphingformulasonehastobeableto“read”algebraicformulas.Furtherresearchisnecessarytoinvestigatewhether graphingformulasindeedimprovesymbolsense,inparticularalgebraicinsightandhowgraphingformulascanbeeffectively andefficientlytaughttostudents.

AppendixA.

Fiveexperts’categorizationsandtheresearcher’scategorizationwithcategorynamesandprototypes.

P.23:22min Q.20:28min R.11:25min S.14:25min T.21:00min Researcher’s

categorization

Linear:ax+b Straightlines:ax+b Linear:ax+b Linear y=x

Linearfunctions Linear

Increasing/decreasing Degree2:ax2_{+bx+c Parabolawithmax:}

−x2

Parabolawithmin:x2

Degree2:ax2_{+bx+c 1turningpoint}

y=x2

Degree2 Parabolawithmaxand withmin

Polynomials:

n

k=0akxk(defined

ondomain)

Degree3(odd):x3 _Degree3: ax3_+bx2_+cx+d

2turningpoints:

y=x3_−3x

Degree3 Degree3increasing

Degree4,decreasing:

−x2_(x2₋₁₎

Degree4,increasing:

x2_(x2₋₁₎

Degree4:ax4_+bx3_{..etc 3turningpoints:}

y=(x2₋₁₎2

5turningpoints y=x2_(x2_−1)(x2₋₂₎

Degree4,with W-shape Degree4without W-shape

Degree4with W-shape M-shape V-shape

Degree6withW-shape (ax+b)k_/(cx+d)n _{Hyperbola:1/x}

Quotientfunctionswith morethan1vertical asymptote: y=1/(x2₋₁₎

Brokenfunctions Verticalandhorizontal asymptotes

y=1/x

Verticaleandslant asymptotesy=x−4/x

2verticalasymptotes: y=1/(x2₋₁₎

Linearbroken:

y=(ax+b)/(cx+d)

Hyperbolaand Powerfunctionwith highernegativeodd exponent

rootfunctionwith transformation: c

right:√x decreasing‘√x

-look-like’

ax2_{+bx+c Power}

functioneven√4

x2

Halfacircle Root Halfacicle:

y=

V-shape:y=

Brokenpowerfunction, nottransformed frombasicfunction

Oddpowerfunction:

3 √

x

Brokenexponent, definedtotheright: x√x

Brokenexponent:ax p

q _{Powerfunction,}

positiveexponent,no asymptote

Powerfunctionwith brokenexponent, concaveup/down

Various:1/ln(x) Apart:1/ln(x) Rest

1/ln(x);(x2₋₁₎−1_;

3(x4_−6)(x2₋₈₎

distractor:1/ln(x)

References

Arcavi,A.(1994).Symbolsense:Informalsense-makinginformalmathematics.FortheLearningofMathematics,14(3),24–35.

Ayalon,M.,Watson,A.,&Lerman,S.(2015).Functionsrepresentedaslinearsequentialdata:relationshipsbetweenpresentationandstudentresponses.

EducationalStudiesinMathematics,90(3),321–339.

Ball,L.,Pierce,R.,&Stacey,K.(2003).Recognisingequivalentalgebraicexpressions:Animportantcomponentofalgebraicexpectationforworkingwith CAS.InternationalGroupforthePsychologyofMathematicsEducation,4,15–22.

Barnard,A.D.,&Tall,D.O.(1997).Cognitiveunits,connectionsandmathematicalproof.InE.Pehkonen(Ed.),Proceedingsofthetwentyfirstinternational conferenceforthepsychologyofmathematicseducation(Vol.2)(pp.41–48).

Barsalou,L.W.(1992).Frames,concepts,andconceptualfields.InA.Lehrer,&E.F.Kittay(Eds.),Frames,fields,andcontrasts:Newessaysinsemanticand lexicalorganization.(pp.21–74).Hillsdale,NJ,England:LawrenceErlbaumAssociates,Inc[vi,464pp.].

Barsalou,L.W.(2008).Groundedcognition.AnnualReviewofPsychology,59,617–645.

Bills,L.,Dreyfus,T.,Mason,J.,Tsamir,P.,Watson,A.,&Zaslavsky,O.(2006).Exemplificationinmathematicseducation.Proceedingsofthe30thconference oftheinternationalgroupforthepsychologyofmathematicseducation,Vol.1,126–154.

Campitelli,G.,&Gobet,F.(2010).HerbertSimon’sdecision-makingapproach:Investigationofcognitiveprocessesinexperts.ReviewofGeneral Psychology,14(4),354.

Carlson,M.,Jacobs,S.,Coe,E.,Larsen,S.,&Hsu,E.(2002).Applyingcovariationalreasoningwhilemodelingdynamicevents:Aframeworkandastudy.

JournalforResearchinMathematicsEducation,22(5),352–378.

Chi,M.T.,Feltovich,P.J.,&Glaser,R.(1981).Categorizationandrepresentationofphysicsproblemsbyexpertsandnovices.CognitiveScience,5(2), 121–152.

Chi,M.T.(2011).Theoreticalperspectives,methodologicalapproaches,andtrendsinthestudyofexpertise.InExpertiseinmathematicsinstruction.pp. 17–39.US:Springer.

Confrey,J.,&Smith,E.(1995).Splitting,covariation,andtheirroleinthedevelopmentofexponentialfunctions.JournalforResearchinMathematics Education,66–86.

Crowley,L.,&Tall,D.O.(1999).Therolesofcognitiveunits,connectionsandproceduresinachievinggoalsincollegealgebra.InO.Zaslavsky(Ed.),

Proceedingsofthe23rdconferenceofPME(Vol.2)(pp.225–232).

DeCorte,E.(2010).Historicaldevelopmentsintheunderstandingoflearning.InH.Dumont,D.Instance,&F.Benavides(Eds.),Educationalresearchand innovationthenatureoflearningusingresearchtoinspirepractice:Usingresearchtoinspirepractice(pp.35–67).OECDPublishing.

deJong,T.,&Ferguson-Hessler,M.G.(1986).Cognitivestructuresofgoodandpoornoviceproblemsolversinphysics.JournalofEducationalPsychology,

78(4),2.

Duval,R.(2006).Acognitiveanalysisofproblemsofcomprehensioninalearningofmathematics.EducationalStudiesinMathematics,61(1–2),103–131.

Eisenberg,T.,&Dreyfus,T.(1994).Onunderstandinghowstudentslearntovisualizefunctiontransformations.InE.Dubinsky,A.Schoenfeld,&J.Kaput (Eds.),Researchincollegiatemathematicseducation(Vol.1)(pp.45–68).Providence,RI:AmericanMathematicalSociety.

Ericsson,K.A.(2006).Protocolanalysisandexpertthought:Concurrentverbalizationsofthinkingduringexperts’performanceonrepresentativetasks.In K.A.Ericsson,N.Charness,P.J.Feltovich,&R.R.Hoffman(Eds.),TheCambridgehandbookofexpertiseandexpertperformance(pp.223–241). Cambridge:CambridgeUniversityPress.

Even,R.(1998).Factorsinvolvedinlinkingrepresentationsoffunctions.TheJournalofMathematicalBehavior,17(1),105–121.

Eysenck,M.W.,&Keane,M.T.(2000).Cognitivepsychology:astudent’shandbook.Taylor&Francis.

Goldenberg,P.,&Mason,J.(2008).Sheddinglightonandwithexamplespaces.EducationalStudiesinMathematics,69(2),183–194.

Gray,E.M.,&Tall,D.O.(1994).Duality,ambiguity:andflexibility:Aproceptualviewofsimplearithmetic.JournalforResearchinMathematicsEducation,

Heid,M.K.,Thomas,M.O.,&Zbiek,R.M.(2012).Howmightcomputeralgebrasystemschangetheroleofalgebraintheschoolcurriculum?InThird internationalhandbookofmathematicseducation.pp.597–641.NewYork:Springer.

Jonassen,D.H.,Beissner,K.,&Yacci,M.(1993).Structuralknowledge:Techniquesforrepresenting,conveying,andacquiringstructuralknowledge.

PsychologyPress.

R,K.(2008).Theinfluenceofsymbolsonpre-calculusstudents’problemsolvinggoalsandactivities(Doctoraldissertation).AvailablefromDissertationsand Thesesdatabase.(UMINo.3329205).

Kieran,C.(2006).Researchonthelearningandteachingofalgebra.InA.Gutiérrez,&P.Boero(Eds.),Handbookofresearchonthepsychologyofmathematics education(pp.11–49).Rotterdam:Sense.

Kilpatrick,J.,&Izsak,A.(2008).Ahistoryofalgebraintheschoolcurriculum.InC.E.Greens,&R.Rubenstein(Eds.),AlgebraandalgebraicThinkinginschool mathematics,seventiethyearbook(pp.3–18).NCTM.

Kop,P.,Janssen,F.,Drijvers,P.,Veenman,M.,&VanDriel,J.(2015).Identifyingaframeworkforgraphingformulasfromexpertstrategies.TheJournalof MathematicalBehavior,39,121–134.

Leinhardt,G.,Zaslavsky,O.,&Stein,M.K.(1990).Functions,graphs,andgraphing:Tasks,learning,andteaching.ReviewofEducationalResearch,60(1), 1–64.

Moschkovich,J.,Schoenfeld,A.H.,&Arcavi,A.(1993).Aspectsofunderstanding:Onmultipleperspectivesandrepresentationsoflinearrelationsand connectionsamongthem.InT.A.Romberg,E.Fennema,&T.P.Carpenter(Eds.),Integratingresearchonthegraphicalrepresentationoffunctions(pp. 69–100).Hillsdale,NJ:LawrenceErlbaumAssociates.

NCTM.(2000).Principlesandstandardsforschoolmathematics.(Accessed14october2014).http://www.nctm.org/standards

Oehrtman,M.,Carlson,M.,&Thompson,P.W.(2008).Foundationalreasoningabilitiesthatpromotecoherenceinstudents’functionunderstanding.InM. P.Carlson,&C.Rasmussen(Eds.),Makingtheconnection:researchandteachinginundergraduatemathematicseducation(pp.27–42).Washington,D.C: MathematicalAssociationofAmerica.

Pierce,R.,&Stacey,K.(2001).Observationsonstudents’responsestolearninginaCASenvironment.MathematicsEducationResearchJournal,13(1),28–46.

Pierce,R.,&Stacey,K.(2004).Aframeworkformonitoringprogressandplanningteachingtowardstheeffectiveuseofcomputeralgebrasystems.

InternationalJournalofComputersforMathematicalLearning,9(1),59–93.

Polya,G.(1945).Howtosolveit.Princeton,NJ:PrincetonUniversityPress.

Presmeg,N.C.(1998).Metaphoricandmetonymicsignificationinmathematics.TheJournalofMathematicalBehavior,17(1),25–32.

Ruiz-Primo,M.A.,&Shavelson,R.J.(1996).Problemsandissuesintheuseofconceptmapsinscienceassessment.JournalofResearchinScienceTeaching,

33(6),569–600.

Ruthven,K.,Deaney,R.,&Hennessy,S.(2009).Usinggraphingsoftwaretoteachaboutalgebraicforms:Astudyoftechnology-supportedpracticein secondary-schoolmathematics.EducationalStudiesinMathematics,71(3),279–297.

Sandefur,J.,Mason,J.,Stylianides,G.J.,&Watson,A.(2013).Generatingandusingexamplesintheprovingprocess.EducationalStudiesinMathematics,

83(3),323–340.

Schwarz,B.B.,&Hershkowitz,R.(1999).Prototypes:Brakesorleversinlearningthefunctionconcept?Theroleofcomputertools.JournalforResearchin MathematicsEducation,362–389.

Sfard,A.,&Linchevski,L.(1994).Thegainsandthepitfallsofreification:Thecaseofalgebra.EducationalStudiesinMathematics,26,191–228.

Sfard,A.(1991).Onthedualnatureofmathematicalconceptions:Reflectionsonprocessesandobjectsasdifferentsidesofthesamecoin.Educational StudiesinMathematics,22(1),1–36.

Slavit,D.(1997).Analternateroutetothereificationoffunction.EducationalStudiesinMathematics,33(3),259–281.

Stylianou,D.A.,&Silver,E.A.(2004).Theroleofvisualrepresentationsinadvancedmathematicalproblemsolving:Anexaminationofexpert-novice similaritiesanddifferences.MathematicalThinkingandLearning,6(4),353–387.

Stylianou,D.A.(2011).Anexaminationofmiddleschoolstudents’representationpracticesinmathematicalproblemsolvingthroughthelensofexpert work:Towardsanorganizingscheme.EducationalStudiesinMathematics,76(3),265–280.

Sweller,J.(1994).Cognitiveloadtheory,learningdifficulty,andinstructionaldesign.LearningandInstruction,4(4),295–312.

Thomas,M.O.,Wilson,A.J.,Corballis,M.C.,Lim,V.K.,&Yoon,C.(2010).Evidencefromcognitiveneurosciencefortheroleofgraphicalandalgebraic representationsinunderstandingfunction.ZDM,42(6),607–619.

Vinner,S.,&Dreyfus,T.(1989).Imagesanddefinitionsfortheconceptoffunction.JournalforResearchinMathematicsEducation,356–366.

Watson,A.,&Mason,J.(2005).Mathematicsasaconstructiveactivity:learnersgeneratingexamples.Mahwah,NJ:LawrenceErlbaum.

Zandieh,M.J.,&Knapp,J.(2006).Exploringtheroleofmetonymyinmathematicalunderstandingandreasoning:Theconceptofderivativeasan example.TheJournalofMathematicalBehavior,25(1),1–17.