Is There a Kuznets Curve?
John Luke Gallup
Portland State University1721 SW Broadway Cramer Hall, Suite 241
Portland OR 97201
jlgallup@pdx.edu
tel: 503-725-3929 fax: 503-725-3945
September 25, 2012
Abstract
No. There has never been good evidence for a pattern of rising inequality in low-income countries and falling inequality in higher income countries. The only evidence that appears to support the Kuznets hypothesis is the cross-sectional pattern of inequality levels across countries, although the Kuznets hypothesis is an assertion about the path of inequality within countries. Numerous cross-sectional studies established the Kuznets curve as a stylized fact, dominating empirical and theoretical research on the effect of economic growth on income inequality since then.
New international panel data with the first internally consistent time series for a large number of countries shows no evidence of a Kuznets curve. The data show an anti -Kuznets curve: inequality decline in low-income countries, and inequality increase in high-income countries. The U-shaped pattern shows up strongly in a non-parametric trend, in stochastic kernel estimation, but weakly in a quadratic fixed effect trend.
JEL Codes: D31, O15, O47
1 Introduction
In late 1954, Simon Kuznets gave a bold Presidential Address to the American Economic Association (Kuznets, 1955). He chose a topic which had been largely unstudied due to lack of data, and used the scant data he had created himself or found elsewhere to propose a law of motion for the distribution of income.
Kuznets had data for the change in income distribution in the United States, United Kingdom, and two states in Germany. The change he was confident of was a sharp decline in inequality in the U.S. and the U.K. after World War I. He also noted substantial income growth in the two countries during the same period.
Kuznets combined his observations about the U.S. and the U.K. with the historical shift from agriculture to industry in the course of economic development to propose a typical pattern of change for income distribution. Kuznets assumed that rural agricultural incomes are lower and more equally distributed than urban industrial incomes. In that case, a shift into nascent industry will raise income inequality, as a rising fraction of workers earn higher industrial wages. Beyond a tipping point, the predominance of industrial employment will improve income distribution, as most workers earn similar industrial wages. This theory predicts an inverted U-shaped relationship between income levels and inequality.
The international income distribution data necessary to evaluate Kuznets’s hypothesis remained severely limited until the mid 1970s. By that time, at least one national income distribution observation was available for enough countries to look at the cross-country relationship between income levels and inequality. The cross-sectional data were consistent with the Kuznets hypothesis: middle-income countries, especially in Latin
America, tended to have higher levels of inequality than low- or high-income countries. This lead to scores of empirical papers over the next forty years looking for an inverted U-shaped curve in cross-country data with gradual improvements in country coverage and econometric technique. A partial list of studies includes Kravis (1960), Paukert (1973), Chenery and Syrquin (1975), Ahluwalia (1976a, 1976b), Saith (1983), Papanek and Kyn (1986), Campano and Salvatore (1988), Ram (1988), Tsakloglou (1988), Bourguignon and Morrison (1990), Anand and Kanbur (1993), Randolph and Lott (1993), Bourguignon (1994), Ogwang (1994), Fields and Jakubson (1995), Ram (1995), Jha (1996), Dawson (1997), Eusufzai (1997), Mbaku (1997), Chang and Ram (2000), Savvidesa and Stengos (2000), Lin and others (2006), and Huang and Lin (2007). The most careful of these studies, such as Anand and Kanbur (1993) and Fields and
Jakubson (1995) did not find robust support for the Kuznets hypothesis, but most did.
None of this research tested Kuznets hypothesis directly: that income inequality would increase and then decrease as income grew within countries. If other factors can
influence the level of income distribution in each country, country characteristics rather than a Kuznets process might explain the cross-sectional pattern.
The shear repetition of cross-sectional results gradually convinced people that the Kuznets curve was an empirical reality, to the point where theorists creating models with income distribution dynamics made sure they were able to replicate a Kuznets curve in their models. By the turn of the century, Kanbur (2000) felt that the dominance of the Kuznets hypothesis in income distribution research had become counter-productive:
In fact, in a strange way the framework set out by the originators may have by now become a straightjacket which inhibits fresh thinking, as every new attempt to model development and distribution does so with at least half an
eye on whether or not the model can, in principle, generate an inverted-U relationship between inequality and development, while most empirical work keeps returning to the question of whether or not there is an inverted-U pattern to be discerned in the data.
Cross-country panel data did not become available until the 1990s. Deininger and Squire (1996, 1998) assembled the first large-scale dataset with enough observations to study the typical path of inequality within countries. Deininger and Squire took the estimates of Gini coefficients from hundreds of separate studies of inequality in individual countries to construct a large number of time series. The two main
conclusions of their research were that more countries have inequality paths inconsistent with the Kuznets hypothesis than consistent, and that most countries’ inequality
changes slowly over time.
Using the Deininger and Squire dataset, researchers have found no support for a Kuznets curve once they control for country fixed effects (Deininger and Squire, 1998, Higgins and Williamson, 1999, Savvidesa and Stengos, 2000, and Barro, 2000). Barro’s
influential paper (updated in Barro, 2008) did find support for the Kuznets curve, but that was due to regressions which do not include country fixed effects. That is, Barro was reproducing the usual cross-sectional patterns. When Barro did include country fixed effects, the quadratic trend in income is insignificant, although the trend becomes statistically significant when he adds a number of additional explanatory variables1. Even then, Barro acknowledges that income levels explain little of the trend in inequality.
1 One can see from a footnote (fn. 24 on p. 31) that the quadratic term in a simple fixed effects regression
Criticism of the accuracy of the inequality time series constructed by Deininger and Squire cast a shadow over research using the data set. The measured level of inequality depends sensitively on the definition of income or expenditure, unit of observation, survey coverage, etc. Combining inequality estimates to construct a time series from studies using different definitions and methods risks introducing spurious jumps due to changes of definition. Atkinson and Brandolini (2003) were skeptical of the accuracy of time series constructed by Deininger and Squire. They showed that for many Western European countries, Deininger and Squire's time series often departed significantly from a series Atkinson and Brandolini constructed using consistent definitions, causing the series to have serious inaccuracies both in the level of inequality and the trend over time. Western European data should presumably be among the most accurate. Atkinson and Brandolini conclude that “we are not convinced that at present it is possible to use secondary datasets [like Deininger and Squire] safely” without evaluating the accuracy of each series within it. Atkinson and Brandolini’s critique effectively ended use of
Deininger and Squire’s panel data in published research due to doubt about the internal consistency of its time series.
This paper uses a new panel of inequality data constructed with consistent definitions and data sources within each country over time. The data are used to estimate two kinds of nonparametric models of the relationship of inequality and income: a non-parametric fixed effects trend and a stochastic kernel model. The estimations show a clear U-shaped relationship rather than Kuznets’ inverted-U relationship.
Several earlier papers have used non-parametric methods to look for a Kuznets curve. Deininger and Squire (1998) in effect does this by counting countries with inverted-U shaped inequality paths. However it not clear that this is a test for a general Kuznets curve if the inverted-U trajectory occurs over different ranges of income in different
countries. Does this imply that countries would undergo multiple inverted-U shaped trajectories as their income rises? Frazer (2006) uses non-parametric regression to test for a Kuznets curve using panel data from an update of the Deininger-Squire dataset. The non-parametric specification does not control for different levels of inequality in each country, however, so his results are still dominated by the cross-sectional levels of inequality. Two other papers (Lin and others, 2006, and Huang and Lin, 2007) use semi-parametric methods to test the Kuznets hypothesis, but by using cross-sectional data, they are also not able to evaluate the typical trend of inequality within countries.
The next section discusses the data in Kuznets’ original paper. Section 3 describes the new inequality data and quadratic trend lines. Section 4 presents a non-parametric fixed effects estimate of the Kuznets curve. Section 5 evaluates change in the distribution of inequality of a panel of countries using stochastic kernel estimation. Section 6 concludes.
2 Kuznets’ data
Kuznets’ hypothesis about the relationship between inequality and economic growth in his 1955 address was based on time-series data for just three countries and his intuition about the mechanisms of economic development. His conjecture was audacious given the data he had to work with. He acknowledged this, saying that his “paper is perhaps 5 per cent empirical information and 95 per cent speculation, some of it possibly tainted by wishful thinking” (Kuznets, 1955, p. 26).
Kuznets used data he helped collect for the United States combined with data for the United Kingdom and two states in Germany. He also found point estimates of
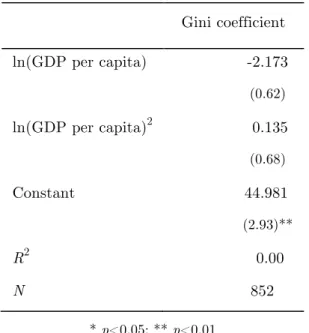
inequality in India, Puerto Rico, and Ceylon. Figure 1 presents the inequality data from Kuznets's original article combined with historical estimates of GDP per capita from
Maddison (2010) to show the patterns he was visualizing. It is striking that his data do not provide much support for his own hypothesis, except that United Kingdom and United States had substantial declines in their inequality before World War II. Kuznets discusses the likelihood that inequality worsened in both of these countries in the
nineteenth century before his time series start, but he had no empirical evidence for it. Besides the U.S. and the U.K, the other countries for which he has inequality estimates do not indicate an inverted-U curve.
Kuznets’ presumption was that inequality is very low in agrarian societies before the advent of industrialization. Pre-modern inequality data are hard to come by, but Milanovic and others (2007) were able to reconstruct inequality data for eleven pre-industrial societies ranging from the Roman Empire in AD14 to China in the 1880s. As shown in Figure 2, inequality in these agrarian societies was not particularly low. All but three of the estimates of inequality are higher than the median inequality in countries today (calculated from the data described in the next section). Half the pre-industrial Gini coefficients are above the 75th percentile of modern inequality estimates, including the estimates of inequality in England and Wales in the 17th and 19th
centuries. The data do not suggest that one can assume low inequality in pre-industrial societies. Feudalism didn’t promote particularly equal distribution.
Kuznets showed that inequality fell in two high-income countries as they grew richer after World War I, but he had no evidence of rising inequality at low income levels. Ironically, Kuznets’ prediction that inequality will rise during the early stages of development, for which he had no evidence, is better remembered than his prediction that inequality will fall at higher incomes.
inequality. In its simplest form, if agricultural workers all earn a low wage and
industrial workers earn an identical higher wage, then the transition from agriculture to industry will create an inverted-U curve in inequality. The movement of the first workers out of agriculture into higher wage industry will increase inequality, but beyond a certain point, inequality will fall as the majority of workers receive the constant industrial wage.
A vulnerability of Kuznets’s theory is that minor changes in the story change the
prediction. For instance, if agricultural incomes are more unequal than industrial wages, perhaps due to unequal land ownership, movement out of agriculture into industry could reduce inequality right away. Furthermore, all kinds of other dynamics of economic development are likely to have implications for inequality besides the movement of labor out of agriculture into industry. International trade, the spread of education, and transportation linking previously isolated regions, to name just a few dynamics, are all likely to have major impacts on income distribution in ways that do not naturally suggest an inverted-U shaped curve.
Besides Kuznets’ scanty data and model of inequality change, what caused his
hypothesis to so thoroughly capture the imagination of economists? The country cross-sectional data.
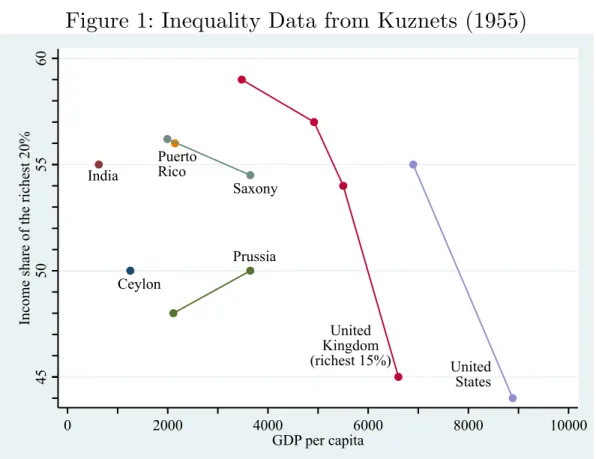
Figure 3 shows recent estimates of inequality for 156 countries. The Gini coefficients are the most recent observation for each country from the panel data set used in this paper for 87 countries augmented with the most recent Gini coefficients for 69 other countries from the World Development Indicators (World Bank, 2011).2 GDP per capita
2 The region categories in Figure 3 and other figures are OECD90, Latin America, Eastern Europe and the
estimates are from the Penn World Tables (Heston et al., 2010).
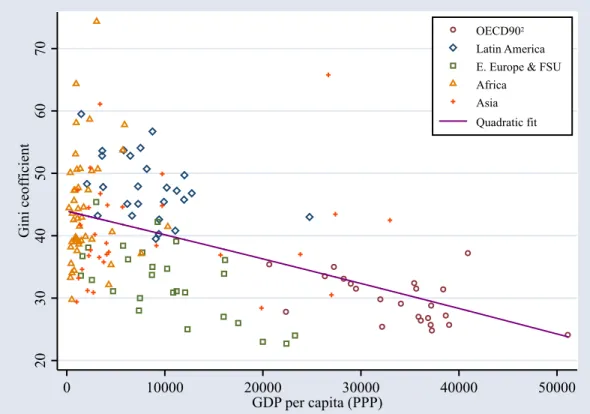
This is the evidence, such as it is, that the Kuznets curve exists. A quadratic fit is significantly concave, although most of the curvature comes from the low inequality levels at high incomes rather than low inequality at low incomes. The curvature is also entirely dependent on using a logarithmic scale for income. Figure 4 shows that the Kuznets curve disappears when the quadratic fit is made using a unit GDP per capita scale rather than a logarithmic scale.
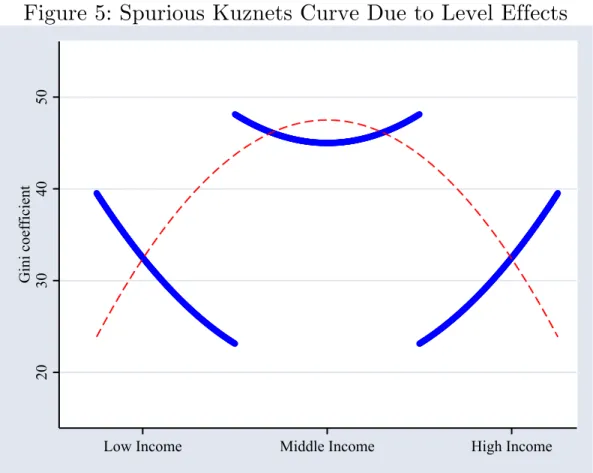
The level of inequality in different countries relative to income does not necessarily tell us anything about the typical path of inequality within countries, which was the object of Kuznets hypothesis. Figure 5 shows that if countries differ in their level of inequality, inequality could follow a U-shaped trend within each country, but the quadratic fit across countries could be an inverted-U curve.
The level of inequality could differ across countries in a simple Kuznets model of
inequality change if some countries have regional variation in incomes and others don’t. If each region industrializes separately, the countries with regional income differences will have higher inequality (due to the interregional income differential) even if every region follows the trajectory of rising then falling inequality in the course of
industrialization.
Looking at within-country inequality trends and allowing for different levels of inequality across countries requires panel data. The panel data assembled for this study is
Cooperation and Development as of 1990, which includes the highest income countries of the world except for oil exporting countries. More recent OECD members Mexico, South Korea, Chile, Israel, Czech Republic, Slovakia, Estonia, Hungary, Poland, and Slovenia are excluded from the OECD90 group, since most of these countries still have income levels substantially lower than OECD90 members. The excluded OECD members countries are included in the other regional groups.
described next.
3 Data and quadratic trends
The lack of comparable data across countries has always plagued research on income inequality. Unlike most other basic national statistics, there is no international organization that collects standardized measures of income distribution worldwide.
Good time series of inequality require data from a uniform household survey design over time because the scope of the questions about household income or household
expenditure can have a big effect on the calculated dispersion of income or expenditure. Surveys should cover the whole countries' population and all sources of income and/or expenditure. Inconsistencies over time in the method used to estimate inequality levels also cause inaccuracies in the time series.
Only very recently have consistently constructed time-series of income distribution become available for a large number of countries. Four organizations have created series of inequality statistics from raw survey data spanning more than a decade for a large number of countries in certain regions of the world. The four organizations are Eurostat (2011) for European Union members, the TransMONEE database created by UNICEF for Eastern Europe and former Soviet Union countries (TransMONEE, 2011), SEDLAC (2011) at the Universidad Nacional de la Plata for Latin America and the Caribbean, and the Luxembourg Income Study database (LIS, 2011) for selected high-income countries. These four organizations provide statistics for all of Europe (East and West), Central Asia, Latin American, and several additional high-income countries.
Major parts of the world still do not have organizations which collect standardized income distribution statistics: East and South Asia, the Middle East, and Africa. Of these, only the Asian regions have a large number of countries with the raw material for the statistics: household income and/or expenditure surveys spanning a substantial number of years.
This study supplements the data from the four regional organizations above with
statistics come from the UNU-WIDER World Income Inequality Database (WIID 2011) and a few other sources. WIID, unlike the other organizations, compiles secondary data rather than generating statistics directly from household survey microdata. WIID is a continuation of the work of Deininger and Squire (1996, 1998) to collect inequality series from national statistical agencies or academic studies. Unlike the original Deininger and Squire data, however, this study does not patch together data from disparate studies into a time series. Crucially, the data in this study only includes country series which are internally consistent over time in terms of the source household survey and the method used to calculate the inequality statistics.
The country times series used in this study hew to the following criteria:
1) They are calculated from surveys of household income (covering all income sources) or household consumption expenditure drawn from a national sample of all households.
2) The time series are calculated from surveys with the same survey design each year.3
3) The time series of inequality statistics are calculated using the same method and definitions within each country.
3 Minor changes of survey questions and survey design still occur over time in many of the standard
national surveys, but statisticians usually address these inconsistencies when they calculate a time series of inequality estimates.
Criteria 2 and 3 are particularly important for ensuring an accurate measurement of the change of inequality over time. Failure to meet these criteria is what caused
inaccuracies in Deininger and Squire's inequality series.
These data cover a later period than the data in Deininger and Squire. Most of the data from Eurostat, TransMONEE, and SEDLAC are derived from national surveys
established in the 1990s which were not available when Deininger and Squire compiled their data. Even most Western European countries did not have annual household income surveys before the establishment of a European-wide survey in 1995.
For the most part, low-income countries measure inequality using household
consumption, and high-income (and Latin American) countries measure inequality using household income. Different countries use different weighting methods for household members. Some use income per adult equivalent, some use income per capita, and a few use total household income. These differences can affect the level of inequality across countries, but that won’t be an issue in this study due to controls for country-specific inequality levels.4
The data include time series from 87 countries, split regionally so that about a quarter of the countries come each from the OECD902, Latin America, Eastern Europe and the Former Soviet Union, and Asia and Africa combined. Asia and especially Africa are underrepresented. The data for Eastern Europe and the former Soviet Union before 1994 are excluded to avoid picking up the sudden inequality changes after the collapse of central planning.
4 See more details about the definitions of inequality in each country in Gallup (2012). It was this kind of
inconsistent definitions within countries which caused the Deininger and Squire data not to have reliable time series.
Gini coefficients are paired with income levels for each country and year. Income levels are measured by gross domestic product (GDP) per capita from the Penn World Tables version 7.0 (Heston and others, 2011). The GDP per capita figures are adjusted for purchasing power parity and reported in 2005 constant international dollars.
The inequality time series for 87 countries are graphed in Figure 6. One can see the inverted-U shape of inequality levels similar to the cross section graph in Figure 3. However, if we control for inequality level differences in each country with a quadratic fixed effects estimator, there is a slight U shape to the fit, although not statistically significant, as shown in Table 1. There is no sign of the inverted U of the Kuznets hypothesis in the typical within-country trend.
Table 1: Fixed Effect Inequality Trend
Gini coefficient ln(GDP per capita) -2.173
(0.62)
ln(GDP per capita)2 0.135
(0.68)
Constant 44.981
(2.93)**
R2 0.00
N 852
* p<0.05; ** p<0.01
In the cross-section, the appearance of an apparent Kuznets curve depends on whether or not GDP per capita is transformed in logarithms. This suggests that testing for a
Kuznets curve may depend sensitively on the functional form used. The next section looks at the relationship of inequality to income level without parametric assumptions about the trend.
4 Non-parametric trend
Kuznets’ hypothesis is about the change in inequality as income grows, not about the level of inequality. Inequality increases at a decreasing rate up to a middle income level and then decreases at an increasing rate. This relationship can be expressed as
dg
dy= f(y) where f(y)≥0 for y≤ym and f(y)<0 for y>ym.
The slope of the trend of inequality, dg
dy, increases up to a middle income, ym, and then decreases. The commonly used quadratic trend line takes f(y)=β1+β2y which implies
that g=β0+β1y+β2y
2 for some β
0, which could be country specific. The Kuznets
hypothesis is that β1>0 and β2<0.
With non-parametric methods, it is not necessary to specify the functional form of f(y);
the shape of f can be inferred from the data. Using m≡dg
dy for the slope of the inequality trend, we can use non-parametric smoothing to fit the equation
mit = f(yit)+εit (1)
to data where εit is a random error, i is the country indicator, and t is the time
indicator. mit = git−gi,t−1
yit−yi,t−1 . Equation 1 is independent of the initial level of inequality in
each country, so it can be used to estimate the typical trend in inequality across countries.
f(⋅) is estimated by kernel-weighted local polynomial smoothing (Stata, 2011, p.
1001-1010). This method takes a weighted polynomial regression of neighboring values to predict the level fˆ(y
it) for each level of income, where yit is the natural log of GDP per
capita.
This method fails due to the large influence of a small number of outliers. In some countries, GDP is virtually unchanged over the period of two inequality surveys. Due to sampling variation, the inequality estimates are different in the two periods, causing the estimate of the slope to explode: for git−gi,t−1 >0 as yit −yi,t−1→0, mit → ∞.
A solution is to smooth each country’s inequality trend separately beforehand, and calculate mit from the smoothed values. Since the ultimate purpose is to find the
average smoothed trend in inequality, smoothing each country’s trend first doesn’t introduce any bias, but it does eliminate the large outliers due to sampling error.
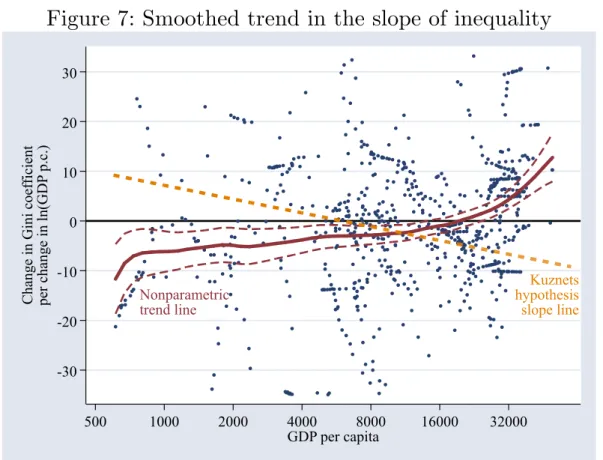
Figure 7 shows the smoothed trend in the inequality slope for different income levels. The dotted lines are the 95% confidence bounds. The results are the opposite of the Kuznets hypothesis. At low income levels, inequality falls with income, and at higher income levels, inequality rises with income.
The preferred specification shown in the figure is a linear smooth (polynomial of degree 1) using an Epanechnikov kernel with a bandwidth determined by the ROT algorithm of 0.46. Under certain assumptions, the ROT bandwidth is optimal (Fan and Gijbels, 1996). The smooth in Figure 7 turned out not to be sensitive to variations in
to 10, with virtually no effect on the smooth. Gaussian, triangle, and rectangle kernels all produced qualitatively similar trends, although the rectangular kernel causes the point of inflection where the slope crosses the axis to occur at a lower income level. A polynomial of degree 0 (local mean smoothing) flattens the trend somewhat, and
polynomials of degree 2 and 3 increase the confidence interval somewhat, but the upward trend remains the same. In each case, the parameters are used for pre-smoothing each of the individual country series are varied along with the final smooth.
To help visualize the results, we can construct a curve in inequality levels from the estimated slope function. Given an estimated slope mˆit = fˆ(yit), the inequality level can
be calculated recursively: gˆit =gˆi,t−1+mˆit(yit −yi,t−1). The level of gi0 is fixed so that the
average level of the curve is equal to the average inequality in the sample. Figure 8 shows the trend line of inequality superimposed on the smoothed country trends. The confidence bounds were calculated by bootstrapping. Like the estimated slope curve, the shape and precision of the level curve is not very sensitive to the choice of bandwidth, kernel, and degree of polynomial.
The non-parametric trend in inequality in Figure 8 shows a strong downward trend in inequality up to relatively high income levels, where the trend becomes upward sloping. The non-parametric trend of inequality is clearly U-shaped, not inverted-U shaped.
The trend in Figure 8 is consistent with Kuznets’ data, such as it was, but it is also consistent with very long historical series that have recently been compiled for top income shares for almost two dozen countries over the course of the twentieth century. Almost all of 22 countries discussed in the survey by Atkinson, Picketty, and Saez (2011) have graphs of the share of income going to the richest 1% over the last hundred years which have remarkably similar shape to the graph in Figure 8, although some
middle European countries and Japan show no sign of the upturn at the end.
5 Stochastic Kernel Estimation
The previous sections used quadratic and non-parametric trends in inequality
(controlling for country fixed effects) to evaluate the change in average cross-country inequality as income grows. A fuller assessment would consider the evolution of the whole distribution of country inequalities as income rises, rather than just the trend. A single trend, for instance, could mask a dynamic where some kinds of countries tend towards one level of inequality and other countries tend towards a different level of inequality. The data show a lot of diversity within countries in the path of inequality, with some countries’ distribution becoming more equal and others less equal whether they start out with high or low inequality.
Stochastic kernel estimation is flexible enough to model the net outcome of complex dynamics of inequality change. It can incorporate a dynamic path where all countries tend towards a single level of inequality or where they tend towards two or more different levels of inequality. It can also incorporate a dynamic path where countries switch places between different levels of inequality, while the overall distribution of cross-national inequalities remains the same.
Stochastic process models are typically applied to processes that evolve over time. However, most hypotheses about income distribution concern the path of inequality as income grows, not as time passes. For this reason, we model the cross-country
distribution of inequalities in the income domain rather than in the time domain.
The stochastic kernel model represents the evolution of continuous distributions from period to period. It is the continuous analogue of a Markov chain, which represents the evolution of discrete distributions. Quah (1997, 2007) explains stochastic kernel models and applies them to the distribution of income levels across countries. Since stochastic kernel models use continuous distribution functions, Quah defines them using measure theory instead of the more accessible matrix algebra of Markov chains.
Continuous income distributions are attractive conceptually, but in practice, stochastic kernel models are estimated by discrete approximation. Digital computers must approximate continuous transition surfaces with discrete grids, so a stochastic kernel model is actually estimated as a fine-grained Markov chain. Since the model is ultimately estimated using a discretized distribution, we will present stochastic kernel estimation using the simpler Markov chain notation. There is no loss of generality since a continuous distribution can be arbitrarily well approximated by a high dimension discrete distribution. Refer to Quah (1997, 2007) for the continuous formulation.
The usual difference in practice between the stochastic kernel and Markov chain estimation is the method of calculating the transition matrix. Markov transition matrices are typically estimated from crude frequency counts of transitions. Stochastic kernel estimation, in contrast, typically uses bivariate kernel density estimation. 5
5 Although stochastic kernel estimation and kernel density estimation both include the term “kernel”,
meaning distribution function, they are referring to different uses of a distribution function. Stochastic kernel estimation refers to the estimation of the transition from one period's distribution to the next period's distribution of the variable of interest (here, inequality). Kernel density estimation refers to the weighting scheme for averaging neighboring frequency observations. The weights decline moving away from the cell of interest according to the value of the kernel, or distribution function, chosen (e.g. Gaussian, Epanechnikov, triangle, etc.)
The stochastic kernel estimation of the transition matrix can be finer-grained with more rows and columns because the kernel density estimation uses information from
neighboring cell frequencies to smooth the density estimates. Whereas a typical Markov transition matrix of frequencies from a sample of several hundred observations might be a 5x5 matrix to avoid small sample sizes in each transition cell, a bivariate kernel density estimator would commonly produce a 50x50 matrix smoothly approximating the surface. So in practice a stochastic kernel estimation is a Markov chain estimation with a smoothed transition matrix.
The Markov chain in this application models the evolution of the distribution of country inequalities with transitions from one income level to another, rather than the more conventional transition from one time period to another. First divide inequality into N possible levels, with values g1,… ,gN . The set G = {g1,… ,gN} is the state space, and countries move from one inequality level, gi, to another, gj , at each step of income.
A fundamental assumption of the Markov model is the Markov property. Let Xs∈G be the inequality level of a country at income level s. The Markov property is that
assumption that E X
(
s+1 X0,…, Xs)
= E X(
s+1 Xs)
. That is, the inequality level at the nexthigher income level depends only on the inequality level at the current income level, and not on the earlier history of inequality levels at lower income levels. In addition, we assume homogeneity of transitions across income levels: E X
(
s+1 Xs)
= E X(
s Xs−1)
for all s.Then we can define the transition probability as pij = E X
(
s+1= gi Xs= gj)
. The N by Nmatrix of all the transition probabilities is P= p⎡⎣ ⎤⎦ij .
Let us be an N-dimensional probability row vector which represents the state of the Markov chain at income level s. The ith component of us represents the probability
that the chain is at inequality level gi. Then us+1=usP. If we assume that for every
inequality level gi except for g1 there is a positive probability of inequality falling to gi−1 at the next income level, and at every inequality level gi except for gN there is a
positive probability of inequality rising to gi+1 at the next income level, these are
sufficient conditions for the Markov chain to be ergodic, which means there is a
possibility of going from every inequality state to every other inequality state, although not necessarily in one step. By Doeblin's Theorem (Stroock, 2000, p. 28), ergodic Markov chains tend towards a unique stationary probability vector as income levels increase without bound. The stationary probability vector w is defined by
w= s→∞ limu0P
s
. w shows us where the distribution of inequalities will end up if the
current distributional dynamic continues indefinitely. The stationary distribution w is
equal to the first left eigenvector of the transition matrix
P
, and is independent of the initial distribution u0 (Theorem 8.6, p. 106, Billingsley, 1979).This Markov model allows for a broad range of inequality dynamics including churning between inequality levels. However, it does rule out a Kuznets curve, the tendency for inequality to rise at low income levels and then switches to moving towards lower inequality beyond a certain income threshold income. The assumption of homogeneity,
E X
(
s+1 Xs)
= E X(
s Xs−1)
, means that if inequality tends to rise with income, it does so atall income levels.
To allow for a Kuznets curve dynamic where inequality increases at low income levels but falls at high income levels, separate Markov processes are estimated for observations below middle income and for those above middle income. The Kuznets hypothesis predicts convergence towards higher inequality levels in the low-income sample and convergence towards lower inequality in the high-income sample.
Estimating the transition matrix requires some conditioning of the data. We need to observe the change in inequality across regular income level intervals. Country
inequality levels are measured at regular time intervals (every year in countries with an annual income survey), not at regular income intervals. To construct a progression of inequality over equally spaced log income intervals, income is quantized into 200 equal log income levels. If more than one sequential inequality observation falls within a given income interval (when income grows too little to progress to the next income level), the inequality observations are averaged.
The categorization of the data into regular income levels produces an inequality “income series” (as opposed to a time series) with a lot of gaps, especially in countries with rapid economic growth, because income may jump several levels between inequality
observations. These gaps are bridged by linear interpolation between income levels in a given country to maintain a connected series (just as observations are typically
connected by straight lines in graphs, like Figure 1). To prevent rapidly growing countries with more interpolated observations having disproportionate influence, the observations are weighted by the number of actual, non-interpolated, data points when estimating the transition matrix. The regridding of inequality takes the original 861 observations and interpolates them up to 2,035 inequality transition observations.
To allow for a different dynamic below and above middle income, the sample is split at the mean income level of $15,000 GDP per capita (rounded to the nearest thousand), and separate transitions are estimated for each subsample. The transition matrices P are estimated using an Epanechnikov bivariate kernel density. The estimation generates 50 by 50 transition matrices which smooth the raw transition frequencies of the Gini
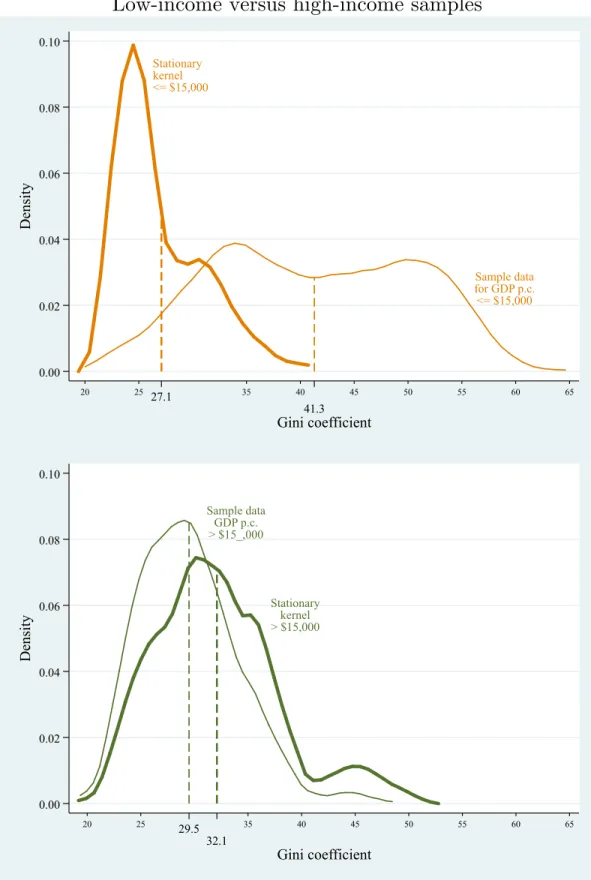
coefficient from one income level to the next. The top panel in Figure 9 displays the stationary kernel for the low-income sample and the bottom panel shows low-income sample, both using an Epanechnikov bivariate kernel with a bandwidth of 3. In each case, the stationary kernel is superimposed on the smoothed distribution of inequalities in the sample.6
The stationary kernel w represents the ultimate distribution of inequality levels if the
transitions observed in the data continue indefinitely. The stationary kernel in low-income countries (the top panel) shows a strong decline of inequality to quite low inequality levels. The stationary kernel for high-income countries (the bottom panel) shows a modest increase in inequality levels compared to the observed sample.
The dotted lines indicate the mean inequality for each distribution. For the low-income sample, the mean inequality has a large statistically significant decline from the observed sample at 41.3 to the stationary distribution at 27.1 (t = 30.98; p = 0.0000), even lower than the mean observed Gini in the high-income sample, at 29.5. In the low-income sample, the mean inequality has a statistically significant rise from the observed sample at 29.5 to the stationary distribution at 32.1 (t = -6.42; p = 0.0000).7
These results are not very sensitive to the choice of kernel or bandwidth for the bivariate kernel density smoothing, but they are quite sensitive to the cut-off point between the low and low-income sample. The same qualitative pattern appears with a Gaussian or a
6 The distributions of observed Gini coefficients in Figure 9 are smoothed with a univariate kernel smoother
using an Epanechnikov kernel with the “rule of thumb” bandwidth of 2.39 for the low-income sample and 1.25 for the low-income sample. The shape of the univariate kernel smooth was not sensitive to the choice of kernel (Epanechnikov, Gaussian, or rectangular) or the bandwidth within a substantial neighborhood of the bandwidth used.
7 The stationary distribution
w is independent of the initial distribution u0, so the difference in means can be tested with an ordinary t test.
rectangle kernel, which are among the common kernels most dissimilar to the Epanechnikov. A similar degree of smoothing requires a lower bandwidth for the Gaussian kernel and a higher bandwidth for the rectangle kernel. Lower bandwidths produce somewhat more compact stationary distributions, with a slightly lower mean for the low-income stationary distribution and a slightly higher mean for the high-income stationary distribution. Higher bandwidths have the opposite effect. The chosen bandwidth of 3 for the Epanechnikov kernel in Figure 9 is the lowest bandwidth which makes the stationary distribution reasonably smooth.
The results are strongly affected by the cut-off point between low income and high income. The lower income sample shows similarly strong convergence to very low inequality levels when the cut-off point between low and high income is lowered, but the convergence becomes weaker as soon as the cut-off point is raised above $15,000. The high-income sample shows convergence to higher inequality with sample cut-offs between $12,000 and $18,000, but outside that range shows almost no distributional change as income grows. This suggests that a cutoff point of $15,000 is about right to distinguish between the falling inequality in low-income countries and the modestly rising inequality in high-income countries.
As with the non-parametric trend in the previous section, the stochastic kernel
estimation shows a clear U-shaped relationship between inequality and income levels, the opposite of Kuznets’ hypothesis. The stochastic kernel estimation allows for more much more complex dynamics than an average trend across countries, but still shows a strong decline in inequality in low-income countries and a modest increase in inequality in high-income countries. The convergence to very low inequality levels is particularly clear in the low-income sample.
6 Conclusion
The empirical analysis using new, higher quality inequality data shows no sign of a Kuznets curve. This confirms the lack of any compelling evidence in the literature that the Kuznets hypothesis describes the typical change in inequality as income grows. There has never been general evidence for the Kuznets hypothesis except for the huge number of cross-sectional studies, which we have no reason to believe capture the typical path of inequality within countries.
Kuznets himself would probably not have been too surprised by the failure to find evidence for the validity of his hypothesis. He was quite clear about the speculative nature of his hypothesis, saying that his “excuse for building an elaborate structure on a such a shaky foundation [of data] is a deep interest in the subject.” (Kuznets, 1955, p. 26)
This study is the first to test the Kuznets hypothesis using internally consistent time series of inequality for a large number of countries. The non-parametric trend and the stochastic kernel estimation both show an anti-Kuznets curve: a strong tendency for inequality to fall with economic growth at low to middle income levels and a weaker tendency for inequality to rise at middle to high income levels. The quadratic fixed effects trend, though convex, is not as clear – it essentially shows no relationship between inequality and income levels.
The U-shaped curve shown in the non-parametric trend and the stochastic kernel estimation is consistent with the twentieth century history of top income shares for a number of currently high-income countries. Most of the 22 countries surveyed in Atkinson, Picketty, and Saez (2011) show the share of income going to the richest 1%
falls during most of the century and then rises somewhat towards the end.
Although there is no sign of a Kuznets curve, a pattern of convergence of inequality as income levels rise is quite clear in the data. This is explored in a separate paper (Gallup, 2012).
It is intriguing to think about what may cause a pattern of inequality change the opposite of that proposed by Kuznets, but I don’t recommend the same devotion to this new pattern that has been given to the original Kuznets curve for fifty years.
References
[1] Ahluwalia, M. S. 1976a. “Income distribution and development: Some stylized facts,” American Economic Review 66(2):128–135.
[2] Ahluwalia, M. S., 1976b. “Inequality, poverty and development,” Journal of Development Economics 3:307–342.
[3] Anand, S. and R. Kanbur. 1993. “Inequality and development: A critique,” Journal of Development Economics 41:19-43.
[4] Atkinson, Anthony Barnes. 1997. “Bringing income distribution in from the cold,” Economic Journal 107(441): 297-321.
[5] Atkinson, Anthony Barnes, and Andrea Brandolini. 2001. “Promise and Pitfalls in the Use of 'Secondary' Data-Sets: Income Inequality in OECD Countries as a Case Study,” Journal of Economic Literature 39: 771-99.
[6] Atkinson, Anthony B., Thomas Piketty, and Emmanuel Saez. 2011. “Top Incomes in the Long Run of History,” Journal of Economic Literature 49(1):3–71.
[7] Barro, Robert J. 2000. “Inequality and Growth in a Panel of Countries,” Journal of Economic Growth 5:5-32.
[8] Barro, Robert J, 2008. “Inequality and Growth Revisited,” ADB Working Paper on Regional Economic Integration No. 11.
[9] Bourguignon, F., 1994. “Growth, distribution, and human resources,” in Ranis, G., ed., En Route to Modern Growth, Essays in Honor of Carlos Diaz-Alejandro. Johns Hopkins Univ. Press, Washington, DC, pp. 43–69.
[10]Bourguignon, F., Morrison, C., 1990. “Income distribution, development and foreign trade: a cross-sectional analysis,” European Economic Review 34:1113–1132.
[11]Campano, F., Salvatore, D., 1988. “Economic development, income inequality, and Kuznets’ U-shaped hypothesis,” Journal of Policy Modeling 10(2):265–280.
[12]Chang, J.Y. & Ram, R. (2000), “Level of Development, Rate of Economic Growth, and Income Inequality,” Economic Development and Cultural Change 48(4):787-99. [13]Chenery, H., and M. Syrquin. 1975. Patterns of development, 1950–1970. London:
Oxford University Press.
[14]Dawson, P. J. 1997. “On testing Kuznets’ economic growth hypothesis,” Applied Economics Letters 4:409–410.
Inequality,” World Bank Economic Review 10(3): 565-91.
[16]Deininger, Klaus, and Lyn Squire. 1998. “New ways of looking at old issues: inequality and growth,” Journal of Development Economics 57: 259-87.
[17]Eusufzai, Z., 1997. “The Kuznets hypothesis: an indirect test,” Economics Letters 54:81–85
[18]Fan, J., and I. Gijbels. 1996. Local Polynomial Modeling and Its Applications. London: Chapman & Hall.
[19]Fields, G. and Jakubson, G. 1994. “New evidence on the Kuznets curve,” mimeo, Cornell University.
[20]Frazer, Garth. 2006. “Inequality and Development Across and Within Countries,” World Development 34(9):1459–1481.
[21]Gallup, John Luke. 2012. “The Global Convergence of Income Distribution,” unpublished.
[22]Huang, Ho-Chuan (River), and Shu-Chin Lin. 2007. “Semiparametric Bayesian inference of the Kuznets hypothesis,” Journal of Development Economics 83:491–505. [23]Heston, Alan, Robert Summers, and Bettina Aten. 2011. Penn World Table Version
7.0, Center for International Comparisons of Production, Income and Prices at the University of Pennsylvania, May 2011.
[24]Higgins, M., & Williamson, J. G. 1999. “Explaining inequality the world round: Cohort size, Kuznets curves and openness,” NBER Working Paper No. 7224. [25]Jha, S., 1996. “The Kuznets curve, a reassessment,” World Development 24(4):773–
780.
[26]Kravis, I. B. 1960. “International differences in the size distribution of income,” Review of Economics and Statistics 42(4):408–416.
[27]Kuznets, Simon. 1955. “Economic Growth and Income Inequality,” American Economic Review 45(1):1-28.
[28]Lin, Shu-Chin, Ho-Chuan (River) Huang, and Hsiao-Wen Weng. 2006. “A semi-parametric partially linear investigation of the Kuznets’ hypothesis,” Journal of Comparative Economics 34:634–647.
[29]LIS. 2011. “Luxembourg Income Study Database: Inequality & Poverty – Key Figures – All Waves.” Accessed 8/5/2011 from http://www.lisdatacenter.org/data-access/key-figures/download-key-figures/. ?
[30]Maddison, Angus. 2010. “Statistics on World Population, GDP and Per Capita GDP, 1-2008 AD.” Accessed 8/26/2011 from
http://www.ggdc.net/MADDISON/Historical_Statistics/horizontal-file_02-2010.xls. [31]Mbaku, J. M. 1997. “Inequality in income distribution and economic development:
Evidence using alternative measures of development,” Journal of Economic Development 22(2):57–67.
[32]Milanovic, Branko, Peter H. Lindert, and Jeffrey G. Williamson. 2007. “Measuring Ancient Inequality.” Munich Personal RePEc Archive, October.
[33]Ogwang, T. 1994. “Economic development and income inequality: A nonparametric investigation of Kuznets’ U-curve Hypothesis,” Journal of Quantitative Economics 10:139-153.
[34]Papanek, G., Kyn, O., 1986. “The effect on income distribution of development, the growth rate and economic strategy,” Journal of Development Economics 23:55–65. [35]Paukert, F. 1973. “Income distribution at different levels of development: A survey of
evidence,” International Labour Review 108:97–125.
[36]Piketty, Thomas. 2006. “The Kuznets Curve,” in Abhijit Banerjee, Roland Bénabou, and Dilip Mookerjee, eds., Understanding Poverty. Oxford: Oxford University Press, pp. 63-72.
[37]Quah, Danny T. 1993a. “Empirical cross-section dynamics in economic growth,” European Economic Review 37:426-434.
[38]Quah, Danny T. 1993b. “Galton's Fallacy and Tests of the Convergence Hypothesis,” The Scandinavian Journal of Economics 95(4):427-443.
[39]Quah, Danny T. 1997. “Empirics for Growth and Distribution: Stratification, Polarization, and Convergence Clubs,” Journal of Economic Growth 2:27–59.
[40]Quah, Danny. 2007. Growth and Distribution. Book draft accessed August 25, 2011 from http://econ.lse.ac.uk/staff/dquah/.
[41]Ram, R. 1988. “Economic development and income inequality: Further evidence on the U-curve hypothesis,” World Development 16:1371-1376.
[42]Ram, R. 1995. “Economic development and inequality: An overlooked regression constraint,” Economic Development and Cultural Change 43:425-434.
[43]Randolph, S. M., and W. F. Lott. 1993. “Can the Kuznets curve be relied on to induce equalizing growth?” World Development 21(5):829–840.
[44]Saith, A. 1983. “Development and distribution: A critique of the cross-country U hypothesis,” Journal of Development Economics 13:367-382.
[45]Savvidesa, Andreas, and Thanasis Stengos. 2000. “Income inequality and economic development: evidence from the threshold regression model,” Economics Letters
69:207–212.
[46]SEDLAC. 2011. “Socio-Economic Database for Latin America and the Caribbean (CEDLAS and The World Bank), July 2011 version - 13. Gini coefficient for the distribution among individuals of different household income variables. Page 1. Equivalized Income D.” Accessed 8/5/2011 from
http://sedlac.econo.unlp.edu.ar/eng/statistics.php.
[47]Tsakloglou, P. 1988. “Development and inequality revisited,” Applied Economics 20:509–531.
[48]TransMONEE. 2011. “The TransMONEE Database, 2011 version.” Accessed 2/16/2011 from http://www.transmonee.org/.
[49]WIID. 2008. “UNU-WIDER World Income Inequality Database, Version 2.0c, May 2008.” Accessed 1/14/2011 from
http://www.wider.unu.edu/research/Database/en_GB/database/.
[50]World Bank. 2011. World Development Indicators. Database accessed August 1, 2011 from http://data.worldbank.org/indicator/SI.POV.GINI.
Figure 1: Inequality Data from Kuznets (1955)
India Ceylon Puerto Rico Saxony Prussia United Kingdom(richest 15%) United States 45 50 55 60 Inc om e s ha re of t he ri che st 20%
0 2000 4000 6000 8000 10000
GDP per capita
n.b. GDP per capita estimates are from Maddison, 2010. The Puerto Rico GDP is for 1950 while the income share is for 1948. Prussia and Saxony use GDP estimates for Germany.
Figure 2: Estimates of Pre-Industrial Income Inequality
Bihar (India) 1807 Brazil 1872
British India 1947
Byzantium 1000 China 1880 England/Wales 1688 England/Wales 1801-3 Holland 1561 Holland 1732
Kingdom of Naples 1811 Moghul India 1750
Nueva Espana 1790
Old Castille 1752
Roman Empire 14 Modern median gini Modern 75th percentile gini
34 43.7 20 30 40 50 60 G ini c oe ffi ci ent
0 1000 1500 1700 1900 Year
Figure 3: Inequality in a Cross Section of Countries with a
Quadratic Fit
20 30 40 50 60 70 G ini c eof fi ci ent250 500 1000 2000 4000 8000 16000 32000 64000 GDP per capita (PPP)
OECD902 Latin America E. Europe & FSU Africa
Asia Quadratic fit
Figure 4: Quadratic Fit of Inequality in a Cross Section of
Countries without a Logarithmic Scale
20 30 40 50 60 70 G ini c eof fi ci ent
0 10000 20000 30000 40000 50000
GDP per capita (PPP)
OECD902
Latin America E. Europe & FSU Africa
Asia Quadratic fit
Figure 5: Spurious Kuznets Curve Due to Level Effects
20
30
40
50
G
ini
c
oe
ffi
ci
ent
Low Income Middle Income High Income
Figure 6: Inequality Time Series Versus Income for 87 Countries
20 30 40 50 60 70
G
ini
c
oe
ffi
ci
ent
1,000 2,000 4,000 8,000 16,000 32,000
GDP per capita (PPP)
OECD902 Latin America
E. Europe & FSU Africa
Figure 7: Smoothed trend in the slope of inequality
Kuznets hypothesis slope line Nonparametric trend line -30 -20 -10 0 10 20 30 Cha nge in G ini c oe ffi ci ent pe r c ha nge in l n(G D P p.c .)500 1000 2000 4000 8000 16000 32000 GDP per capita
Figure 8: Non-parametric trend in inequality
20 30 40 50 60 70 G ini c oe ffi ci ent
1000 2000 4000 8000 16000 32000
GDP per capita
OECD902 Latin America
E. Europe & FSU Africa
Figure 9: Stochastic kernel estimation of inequality distribution
Low-income versus high-income samples
Sample data for GDP p.c. <= $15,000 Stationary
kernel <= $15,000
0.00 0.02 0.04 0.06 0.08 0.10
D
ens
it
y
20 25 27.1 35 40 45 50 55 60 65
41.3
Gini coefficient
Sample data GDP p.c. > $15_,000
Stationary kernel > $15,000
0.00 0.02 0.04 0.06 0.08 0.10
D
ens
it
y
20 25 29.5 35 40 45 50 55 60 65
32.1