How does Investors' Legal Protection affect Productivity and Growth?
Full text
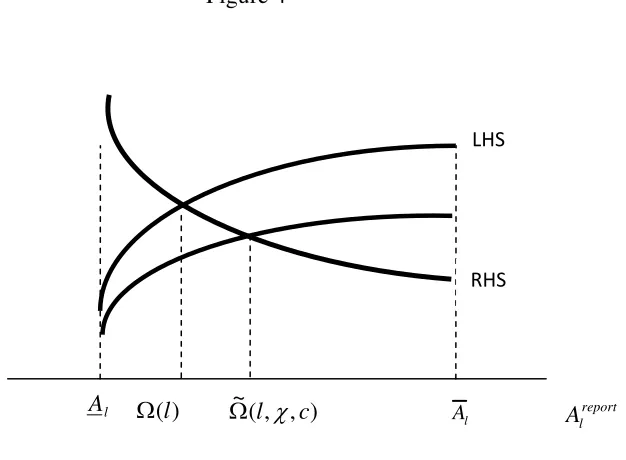
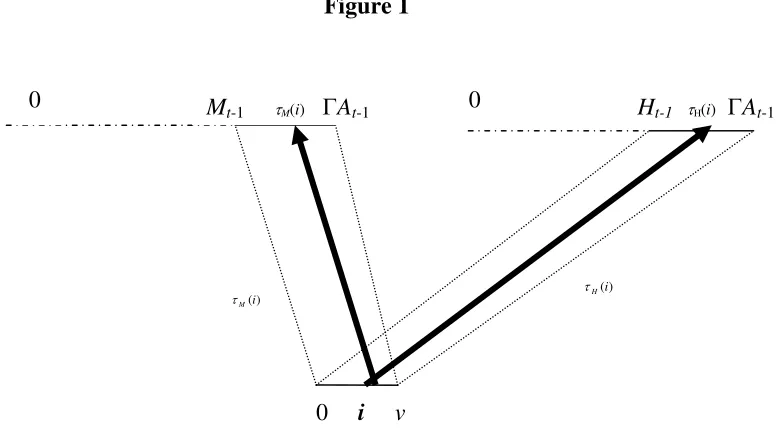
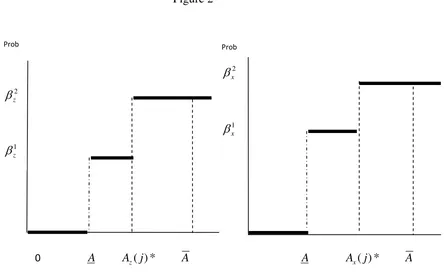
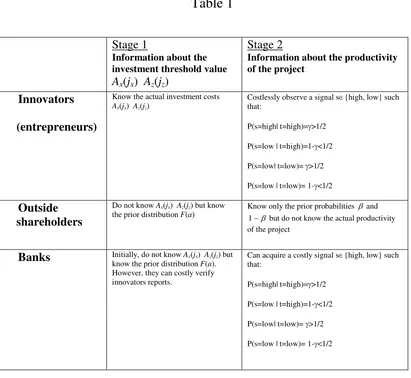
Figure
Related documents
• Final in-person consultation at venue 2-4 weeks prior to wedding date. • Includes all items listed in the month-of package with the addition of: •
For this purpose, this research analyzes empirical relationship between fiscal capacity and poverty rate using panel data for all local governments in
The definition of target audiences for press work requires the identification of those persons, groups, or sectors of the society that the group organizing an advocacy
Morphologically, the sea urchin sperm AR consists of the fusion of the membrane around the acrosomal vesicle with the sperm plasma membrane (exocytosis), to expose the adhesive
Navman Europe Limited Sales of MiTAC International products, provision of after-sales service.. Tyan Computer Corporation - USA Sales of MiTAC International products, provision
George is portrayed (Fig. 4), with the bold highlights, the light pink on the cheeks, and even the detail of the light glow- ing on the neck, together with the icon’s
The findings from this study suggest that few family child care providers have a college degree (associate’s or higher) or a Rhode island early Learning Standards Certificate, both
Ruspolia nitidula (Scopoli, 1786) and Mecostethus parapleurus (Hagenbach, 1822) are species with similar requirements – both are hygrophilous and prefer mainly wet lowland meadows