Spatial modelling of emergency service response times
Full text
Figure




Related documents
The purpose of this research was concentrated on analyzing the satisfaction degree as perceived by patients within public and private medical systems from Oradea, Romania;
The purpose of this study was to discover what female collegiate athletes find to be the most helpful verbal communications and non-verbal communications from their coaches
Since price Lorenz dominance is equivalent to univariate Lorenz order of expenditures, whatever the prices, it is tantamount saying that for any prices there exists a series of
Finally, our third major finding is that, although crowd wisdom was absent from the (choice) conditions that predicted game outcomes against point spreads, predictions were
Methods: Methanol content of suspected alcoholic beverages referred to forensic toxicology laboratory, Guilan province, Iran was measured using gas chromatography and a
Based on the results of the analysis, many of the problems blind users had in the previous study can be generalised to other shopping websites and previous research that points
Sáám stel die denkers ’n mens in staat om waardes se plek, aard en status (gesag) duideliker te omskryf. Dit sal gedoen word in enkele samevattende stellings, wat moontlik
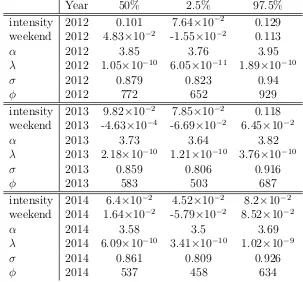
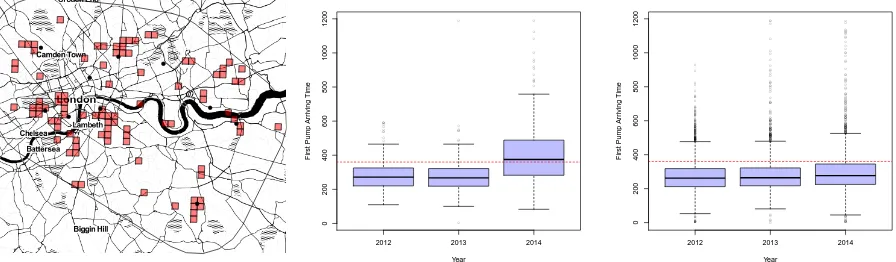
![Figure 6:Plots showing E[S(360, s)], the expected probability that the response time willbe greater than 360 seconds for each location s that is within the Greater London region;top left: for the year 2012, top right: for the year 2013 and in the bottom pl](https://thumb-us.123doks.com/thumbv2/123dok_us/9383234.441483/14.612.73.531.137.579/figure-expected-probability-response-seconds-location-greater-london.webp)
![Figure 7:Top row: the left plot shows P[S2014(360, s) > S2012(360, s) + 0.1] and the rightplot shows P[S2014(360, s) > S2012(360, s) + 0.25]](https://thumb-us.123doks.com/thumbv2/123dok_us/9383234.441483/16.612.71.494.78.638/figure-row-left-plot-shows-rightplot-shows-s.webp)
![Figure 8:Top: P[S2014(360, s) > S2012(360, s) + 0.1].Middle Top: P[S2014(360, s) >S2013(360, s) + 0.1]](https://thumb-us.123doks.com/thumbv2/123dok_us/9383234.441483/17.612.140.474.78.642/figure-top-p-s-s-middle-top-p.webp)