Comparison of Design and Analysis of Concrete Gravity Dam
Full text
Figure

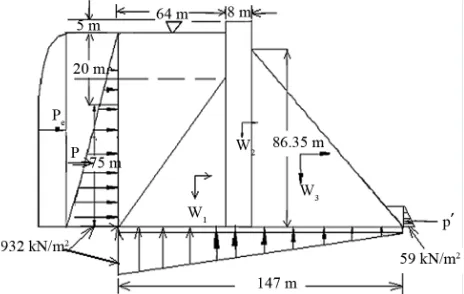

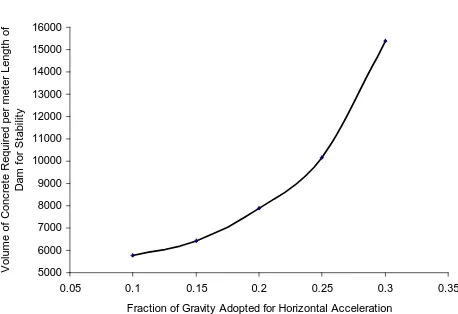
Related documents
Field experiments were conducted at Ebonyi State University Research Farm during 2009 and 2010 farming seasons to evaluate the effect of intercropping maize with
Indeed, legumes play central roles [ 112 ]: (1) at food-system level, both for human and animal consumption, as a source of plant pro- teins and with an increasingly importance
An important question in managing patients with prior anti- NMDAR encephalitis concerns the duration of long-term monitoring after the initial episode to facilitate early
(a) Empirical values by year and species (averaged across cohorts and microhabitats); (b) empirical values by year and microhabitat (averaged across species and cohorts). Retained
It was decided that with the presence of such significant red flag signs that she should undergo advanced imaging, in this case an MRI, that revealed an underlying malignancy, which
Also, both diabetic groups there were a positive immunoreactivity of the photoreceptor inner segment, and this was also seen among control ani- mals treated with a
Nutritional evaluation of rapeseed protein isolate as fish meal substitute for juvenile turbot ( Psetta maxima L.) — Impact on growth performance, body
19% serve a county. Fourteen per cent of the centers provide service for adjoining states in addition to the states in which they are located; usually these adjoining states have