Scheduling Data-Driven Workflows in Multi-Cloud Environment
Full text
Figure

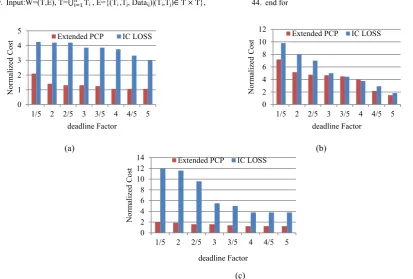
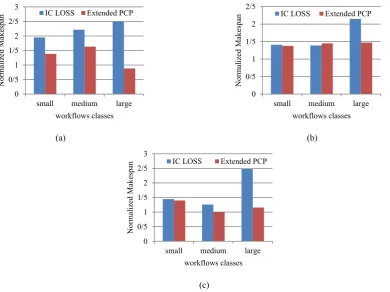

Related documents
Field experiments were conducted at Ebonyi State University Research Farm during 2009 and 2010 farming seasons to evaluate the effect of intercropping maize with
MAP: Milk Allergy in Primary Care; CMA: cow’s milk allergy; UK: United Kingdom; US: United States; EAACI: European Academy of Allergy, Asthma and Clinical Immunology; NICE:
It was decided that with the presence of such significant red flag signs that she should undergo advanced imaging, in this case an MRI, that revealed an underlying malignancy, which
Also, both diabetic groups there were a positive immunoreactivity of the photoreceptor inner segment, and this was also seen among control ani- mals treated with a
The most important contributions of this paper are (i) the proposal of a concern mining approach for KDM, what may encourage other groups to start researching on
4-RUU is an over-constrained PM,it has beenproventhat 4-RUU mechanism has three operation modes with Study's kinematic mapping of the Euclidean group se(3) dual quaternion
19% serve a county. Fourteen per cent of the centers provide service for adjoining states in addition to the states in which they are located; usually these adjoining states have
Police use of public video surveillance in Germany from 1956: management of traffic, repression of flows, persuasion of