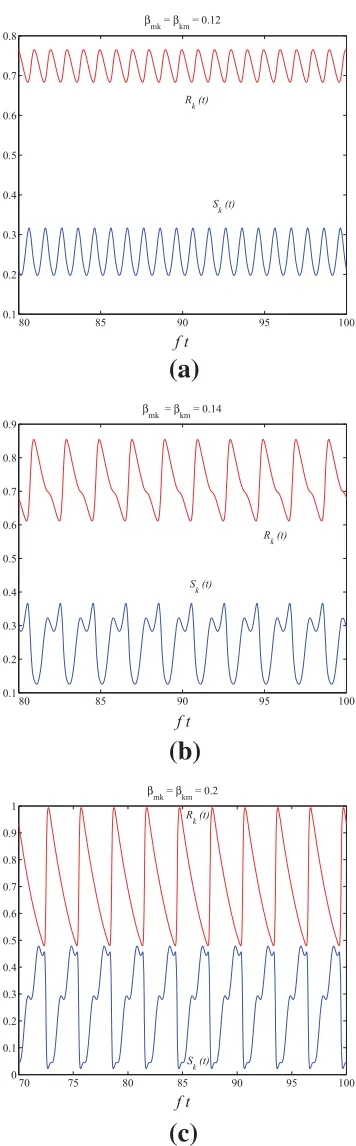
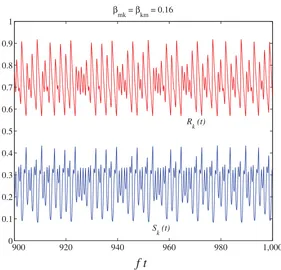
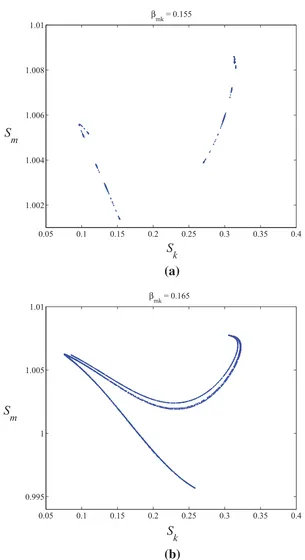
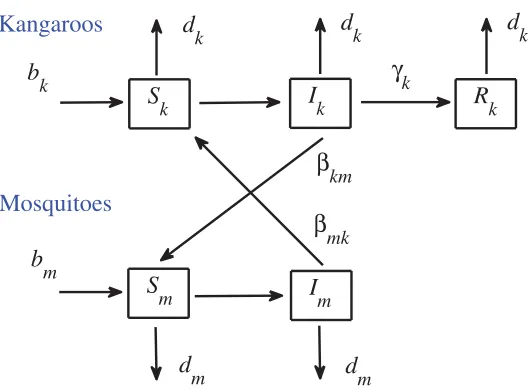
A model for the dynamics of Ross River Virus in the Australian environment
Full text
Figure
Related documents
Field experiments were conducted at Ebonyi State University Research Farm during 2009 and 2010 farming seasons to evaluate the effect of intercropping maize with
After successfully supporting the development of the wind power technology, an approach is needed to include the owners of wind turbines in the task of realizing other ways, other
Мөн БЗДүүргийн нохойн уушгины жижиг гуурсанцрын хучуур эсийн болон гөлгөр булчингийн ширхгийн гиперплази (4-р зураг), Чингэлтэй дүүргийн нохойн уушгинд том
19% serve a county. Fourteen per cent of the centers provide service for adjoining states in addition to the states in which they are located; usually these adjoining states have
The paper is discussed for various techniques for sensor localization and various interpolation methods for variety of prediction methods used by various applications
It was decided that with the presence of such significant red flag signs that she should undergo advanced imaging, in this case an MRI, that revealed an underlying malignancy, which
Also, both diabetic groups there were a positive immunoreactivity of the photoreceptor inner segment, and this was also seen among control ani- mals treated with a
Eksperimenti su pokazali da je za mutiranu tRNA Trp , koja nosi supstituciju u D-ruci, smanjena točnost procesa translacije na način da su reakcije koje se odvijaju