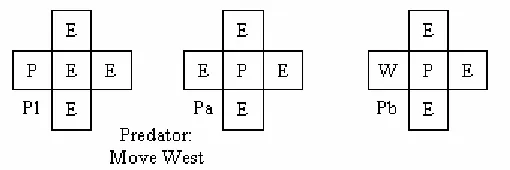
The Apriori Stochastic Dependency Detection (ASDD) algorithm for learning Stochastic logic rules
Full text
Figure



Related documents
Similar study was also conducted by Paul D Larson et al [5] and they reported that buyer used greater relational exchange and electronic communication media with large
The transformation tool ODM2CDA was integrated as a web service into the portal of medical data models [14], therefore all available forms (>9.000) can be exported in CDA format..
Indichi per favore quante volte nelle ultime 4 setti- mane ha evitato grandi di consumare quantità di cibo?. |1| Non ho mai evitato grandi quantità di cibo |2| Non ho quasi mai
The reduced feed intake on the 0.25 % unripe noni powder and subsequent improvement on the 0.25 % ripe powder was not clear but palatability problems due to possible compos-
The process of iris texture classification typically involves the following stages: (a) estimation of fractal dimension of each resized iris template (b) decomposition of template
This paper proposes a tolerant control for the open- circuit fault of the outer switches in three-level rectifiers (both 3L-NPC and T-type topologies) used in
CUAJ ? July August 2014 ? Volume 8, Issues 7 8 ? 2014 Canadian Urological Association Ryan Kendrick Flannigan, MD;* Geoffrey T Gotto, MD, FRCSC;? Bryan Donnelly, MD, FRCSC;? Kevin