Generalising the Discriminative Restricted Boltzmann Machine
Full text
Figure



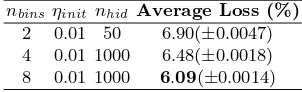
Related documents
Proprietary Schools are referred to as those classified nonpublic, which sell or offer for sale mostly post- secondary instruction which leads to an occupation..
In the simplest scheme based on the boolean model for retrieval, we retrieve the documents that have occurrences of both good and teacher.. Such
○ If BP elevated, think primary aldosteronism, Cushing’s, renal artery stenosis, ○ If BP normal, think hypomagnesemia, severe hypoK, Bartter’s, NaHCO3,
more than four additional runs were required, they were needed for the 2 7-3 design, which is intuitive as this design has one more factor than the 2 6-2 design
4.1 The Select Committee is asked to consider the proposed development of the Customer Service Function, the recommended service delivery option and the investment required8. It
Considering a range of tax and benefit systems, particularly those having benefit taper rates whereby some benefits are received by income groups other than those at the bottom of
Results suggest that the probability of under-educated employment is higher among low skilled recent migrants and that the over-education risk is higher among high skilled
• Follow up with your employer each reporting period to ensure your hours are reported on a regular basis?. • Discuss your progress with