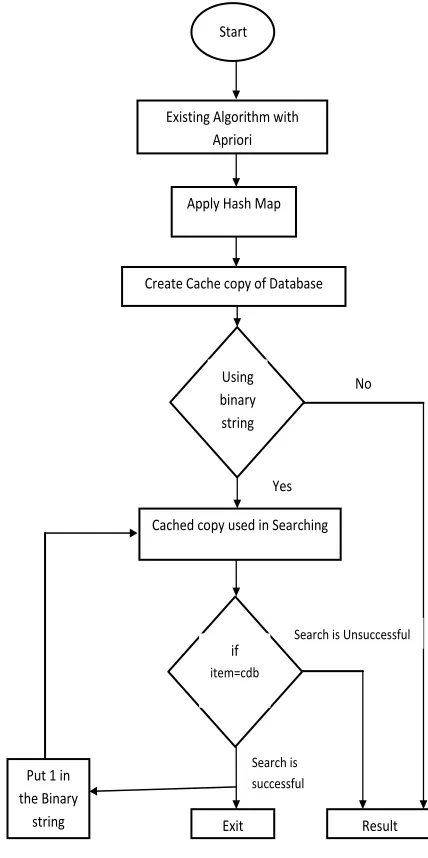
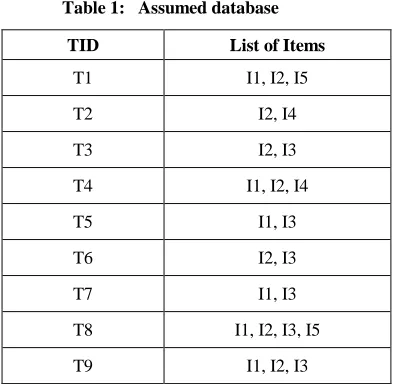
Improving Efficiency of Apriori Algorithm using Cache Database

e st = l chain + d buoy − z ± η cos ε, (4) with e st the extension at the moment of slack tide (related to high- or low-water slack), l chain the length of the chain, d buoy the

More specifically, it was observed that the consequences of education on mortality are more severe among whites than African Americans and Hispanics, but the

**Fill the boiler completely with water, watching for leaks at all plumbing connections. **Open all valves and turn on the pump. Watch for leaks. Let the pump run until all the air

In-depth interviews were used to collect primary data from officials (policy implementers) in the Ministry of Health and Social Welfare, National AIDS Control Program,

Specifically, we describe OMB Budget Guidance, the Federal Data Center Consolidation Initiative (FDCCI), the 25 Point Implementation Plan to Reform Federal Information

Teknik penjarian variasi petikan arpeggio, dinamakan pinch (double-stop) yaitu teknik memetik jari jempol dengan jari antara i-m-a maupun bervariasi antara tiga atau empat

Due to the fast growing world population and reduction of scarce resources, the attentions of nations have been shifted to the marine related resources as

• tools and data that directly support your response procedures, such as an isolated com- puter system to test artifacts that were found on compromised systems, and a contact