ISSN Online: 2327-4379 ISSN Print: 2327-4352
DOI: 10.4236/jamp.2019.711185 Nov. 8, 2019 2712 Journal of Applied Mathematics and Physics
An Algorithm for Generating Random Numbers
with Normal Distribution
Pirooz Mohazzabi, Michael J. Connolly
Department of Mathematics and Physics, University of Wisconsin-Parkside, Kenosha, WI, USA
Abstract
A new algorithm is suggested based on the central limit theorem for generat-ing pseudo-random numbers with a specified normal or Gaussian probability density function. The suggested algorithm is very simple but highly accurate, with an efficiency that falls between those of the Box-Muller and von Neu-mann rejection methods.
Keywords
Random Numbers, Central Limit Theorem, Normal Distribution, Gaussian Distribution
1. Introduction
Random numbers are extremely important in all areas of computational science. As a result, any programming compiler comes with some sort of pseudo-random number generator that normally generates random numbers that are uniformly distributed in the interval
[ )
0,1 . However, in many situations, one requires ran-dom numbers that have nonuniform distribution.Let us suppose that we want to generate random numbers that are distributed according to the probability density function p x
( )
. This can be systematically achieved by first finding the cumulative probability distribution function P x( )
according to [1] [2],( )
x( )
dP x =
∫
−∞p u u (1)and then solving the equation
( )
P x =r (2)
for x in terms of r, where r is a uniform random number in the unit interval 0≤ <r 1. The random numbers x that are generated by this so-called inverse
How to cite this paper: Mohazzabi, P. and Connolly, M.J. (2019) An Algorithm for Generating Random Numbers with Normal Distribution. Journal of Applied Mathemat-ics and PhysMathemat-ics, 7, 2712-2722.
https://doi.org/10.4236/jamp.2019.711185
Received: October 6, 2019 Accepted: November 5, 2019 Published: November 8, 2019
Copyright © 2019 by author(s) and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/
DOI: 10.4236/jamp.2019.711185 2713 Journal of Applied Mathematics and Physics transform method are distributed according to the probability density function
( )
p x .For example, consider the exponential probability density function,
( )
1e if 00 if 0
x x p x x λ λ − ≥ = < (3)
where
λ
is a constant. We have( )
1 0e d 1 e
x x x
P x λ x λ
λ − −
=
∫
= − (4)Then solving
1 e− −xλ =r (5)
we get
(
)
ln 1
x= −λ −r (6)
Thus, if r is a uniformly distributed random number in the unit interval 0≤ <r 1, then x is a random number distributed according to the exponential density function (3).
In principle, the inverse transform method generates random numbers with any probability density function. However, the method relies on two conditions. First, the integral in Equation (1) should be evaluated analytically and, second, one should be able to solve Equation (2) explicitly for x in terms of r. But these are not always possible. For example, the Gaussian or normal probability density function,
( )
( )2 2 22
1 e 2
x
p x µ σ
σ
− −
=
π (7) is a function for which the integral in Equation (1) cannot be evaluated analyti-cally. However, based on the Gaussian density function, one can generate a two- dimensional probability density, and then transform it into plane polar coor-dinates. After some simple algebraic manipulations, one obtains the random numbers
( )
1 2( )
1 22 cos and 2 sin
x=
ρ
θ
y=ρ
θ
(8)each of which is distributed according to the Gaussian probability density (7) [1]. Here
ρ
is a random number generated according to the exponential distribu-tion (3) andθ
is uniformly distributed in the interval 0≤ < πθ
2 . This algo-rithm is known as the Box-Muller method.DOI: 10.4236/jamp.2019.711185 2714 Journal of Applied Mathematics and Physics Figure 1. Probability density function p x
( )
and aconstant comparison function c x
( )
for generating random numbers by acceptance-rejection method.defines a point within the rectangle shown in Figure 1. If y< p x
( )
, this point is below the curve p x( )
and the random number x is accepted, otherwise, it is rejected. The process is then repeated. The random numbers x thus generated have the probability density function p x( )
. Clearly the rejection method works for any arbitrary probability density function.Because the normal or Gaussian probability distribution is the most encoun-tered distribution in nature, in this work we suggest yet another algorithm for generating random numbers with normal probability density function that is based on the central limit theorem.
The organization of the contents of this article is as follows: In Section 2, we develop the theoretical foundation for the investigation. In Section 3, we discuss random numbers with normal distribution, and suggest a new algorithm for their generation followed by computer simulation results. In Section 4, we com-pare the suggested algorithm with other algorithms in terms of accuracy and speed. Finally, in Section 5, we present a summary of the current investigation followed by concluding remarks.
2. Theory
Consider a random number x that is distributed according to the normalized probability density function p x
( )
. The expected value or the mean value of x and x2 are given by [6]( )
dx =
∫
xp x xD (9)
and
( )
2 2
d
x =
∫
x p x xD (10)
where D is the domain of p x
( )
. Then, the variance of the distribution is given by2
2 2
x x x
σ = − (11)
Now let us pick n of these random numbers and find their average
1 1
1 n i i
y x n =
DOI: 10.4236/jamp.2019.711185 2715 Journal of Applied Mathematics and Physics Then, repeat this process a large number of times with the same number n to generate y y y1, 2, 3,. The question is, are the new random numbers y as
ran-dom as the numbers x? In other words, is the probability density function for y the same as p x
( )
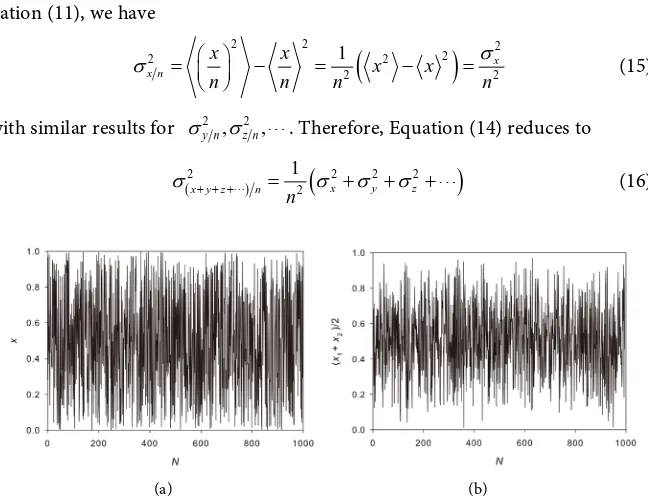
? The answer is no. The new random numbers y are not as random as the numbers x. For example, consider a random number x that is un-iformly distributed in the interval 0≤ <x 1. Figure 2(a) shows the graph of 1000 of these random numbers. We then generate 1000 pairs of these numbers and plot the average of them, which is shown in Figure 2(b). As can be seen from these figures, although both systems have a mean of 0.5, the random num-bers generated by the average of pairs of the uniformly distributed numnum-bers are generally closer to their mean than the former ones, and hence they have a dif-ferent probability distribution function.Let x y z, , , be several uncorrelated random variables with corresponding probability density functions f x
( ) ( ) ( )
,g y ,h z ,. Let the variances of these random variables be 2 2 2, , ,
x y z
σ σ σ
, respectively. Then according to the Bienayméformula [7],
2 2 2 2
x y z x y z
σ
+ + +=σ
+σ
+σ
+ (13)where 2 x y z
σ + + + is the variance of the random numbers generated by the sum of
the random variables x y z, , ,. From this equation, we find the variance of the average
(
x+ + +y z )
n,(2x y z )n = x n2 2y n 2z n
σ + + + σ +σ +σ + (14)
where n is the number of random variables to be averaged. But according to Eq-uation (11), we have
(
)
2 2 2
2
2 2
2 2
1 x
x n
x x
x x
n n n n
σ
σ = − = − =
(15)
with similar results for 2 2
, ,
y n z n
σ
σ
. Therefore, Equation (14) reduces to(2 ) 2
(
2 2 2)
1
x y z
x y z n
n
σ + + + = σ +σ +σ + (16)
[image:4.595.212.536.438.687.2](a) (b)
DOI: 10.4236/jamp.2019.711185 2716 Journal of Applied Mathematics and Physics Finally, if all the random variables have the same distribution, we get
2 2 2 2 2 2 2
x y z n
σ +σ +σ +=σ +σ +σ += σ (17)
And, if for the sake of simplicity we denote σ(2x y z+ + +)n by 2 n
σ , Equation (14) reduces to
n
n
σ
σ = (18)
Furthermore, it can also be shown that the mean of these random numbers is the same as the mean of the original random numbers, i.e.,
n
x = x (19)
As an example, the normalized probability density function for a random number that is uniformly distributed over the interval
[ )
0,1 is p x( )
=1. Then,1 2
x = (20)
and
2 1
3
x = (21)
Therefore,
2
1 1 1
3 2 2 3
σ = − =
(22)
Therefore,
2
1
2 2 6
σ
σ = = (23)
This explains why the random numbers in Figure 2(b) are less random than those in Figure 2(a). Likewise, if we average n of the uniformly distributed ran-dom numbers in the interval
[ )
0,1 to obtain new random numbers, we obtain1 1
and
2 2 3
n n
x
n
σ
= = (24)
According to the central limit theorem, the random numbers thus obtained tend toward normal or Gaussian distribution as n→ ∞ [8] [9] [10] [11]. In
fact, according to this theorem, the shape of the initial distribution of the ran-dom numbers is immaterial and the distribution of the mean approximates a normal distribution if the sample size is sufficiently large, with a mean and standard deviation given by Equations (18) and (19) [12]. It is also worth noting that as n→ ∞, σ →n 0, the resulting normal distribution approaches the Di-rac delta function [13] [14] [15].
DOI: 10.4236/jamp.2019.711185 2717 Journal of Applied Mathematics and Physics [16] [17]. However, most generators use the linearcongruential or power resi-due method and generate pseudo-random numbers in the interval
[ )
0,1 , which is perhaps the most convenient interval in many applications [18] [19] [20].Figures 3-5 show the results of computer simulations for progression to-ward a normal or Gaussian distribution for n=2, n=3, and n=20 starting with a uniform initial distribution in the interval
[ )
0,1 . In each case 106 random numbers are generated. The corresponding probability density function for a normal distribution with mean and standard deviation given by Equations (24) is also shown for comparison in each case. As can be seen from Figure 5, the agreement between the sample mean of 20 random numbers with Gaussian dis-tribution is nearly perfect. Therefore, excellent Gaussian approximations can be achieved with fairly small samples.In Figure 5, the mean and standard deviation of p x
( )
for the sample means and the Gaussian distribution are both µ =1 2 and σ =1 240, respectively. This is due to the fact that the mean and the standard deviation in this case are given by Equations (24). Furthermore, because n is an integer, the standard dev-iation is quantized, with values given by1
, 1, 2, 3, 2 3
n n
n
σ = = (25)
But this is certainly a limitation because we may need to generate random num-bers that have Gaussian distribution with an arbitrary mean
µ
and standard deviationσ
that are not necessarily one of these quantities.Let us suppose that we need to generate random numbers with Gaussian dis-tribution given by Equation (7), with arbitrary values of the mean
µ
and stan-dard deviationσ
. We start by generating uniform random numbers in the interval[ )
0,1 , and take the average of n of these numbers, say 20 of them, to generate new random numbers with Gaussian distribution as in Figure 5. The random numbers thus generated have a mean 1/2 and a standard deviation 1 2 3n.To adjust the generated random numbers to match the specified Gaussian distribution, we have to change two things; the mean
µ
and the standard dev-iationσ
. The standard deviation needs to be adjusted first. To do so, we divide each random number by 1 2 3n and multiply by the requiredσ
. Thus, we multiply each of the random numbers by a factorα
, where2 3
1 2 3n n
σ
α = = σ (26)
This changes the standard deviation to the required value. But this also changes the mean from 1/2 to
1 3
2 n
µ α= = σ
(27)
We now have to shift the mean to the required value
µ
. This is done by shifting each of the new random numbers byδ
x, given by3
x n
DOI: 10.4236/jamp.2019.711185 2718 Journal of Applied Mathematics and Physics Figure 3. Probability density generated by averaging two
random numbers from a uniform distribution in the interval
[
0,1)
(the bullets). The solid curve is the Gaussian function with the same mean and standard deviation calculated from Equation (24).Figure 4. Same legends as in Figure 3 but with averaging three random numbers.
Figure 5. Same legends as in Figure 3 but with averaging twenty random numbers.
The random numbers thus generated have the required normal or Gaussian dis-tribution.
Combining the above transformations, if x is the average of n uniformly dis-tributed random numbers in the interval
[ )
0,1 , then x′ obtained through the transformation(
)
3 2 1
x′ = n
σ
x− +µ
(29) [image:7.595.290.456.277.395.2] [image:7.595.292.459.439.566.2]DOI: 10.4236/jamp.2019.711185 2719 Journal of Applied Mathematics and Physics
( )
( )2 2 22
1 e 2
x
p x µ σ
σ
′
− −
′ =
π (30) As an example, suppose we want to generate random numbers having a nor-mal probability distribution with µ= −2 and
σ
=1.0, i.e.,( )
( )22 2
1 e 2
x
p x = − +
π (31)
To do so, we generate random numbers x so that each is the average of 20 un-iformly distributed random numbers in the interval
[ )
0,1 . We then transform these into new random numbers x′ according to Equation (29), which reduces to(
)
2 15 2 1 1
x′ = x− − (32)
These calculations can be performed using any computer programming lan-guage, such as Python. The random numbers x′ thus generated have the re-quired probability distribution, as shown in Figure 6.
4. Comparison with Other Algorithms
As stated earlier, throughout the computer simulations 106 random numbers were generated. These numbers were then placed in bins, each of width dx=0.01. The bin contents were then normalized and plotted in the figures described above.
In order to compare the suggested algorithm with the Box-Muller and the von Neumann rejection methods, we investigated two measures; accuracy and effi-ciency. For accuracy, we considered the root-mean-square deviation between the bin contents and the values of the corresponding normal distribution for each algorithm. In doing so, we compared the probability density functions in differ-ent intervals about the mean of the distribution, namely, µ±0.5σ , µ σ± ,
2
µ± σ, µ±3σ, µ±4σ , and µ±5σ. We have considered several intervals because the fluctuation of the bin contents is normally higher near the peak of the distribution. The results are shown in Table 1 for µ=0, which clearly shows the accuracy of the three algorithms is nearly identical in all cases.
[image:8.595.291.461.538.667.2]DOI: 10.4236/jamp.2019.711185 2720 Journal of Applied Mathematics and Physics Table 1. Root-mean-square deviation between the bin contents and the values of the corresponding normal distribution for the suggested algorithm, the Box-Muller, and the von Neumann rejection algorithms.
Root-Mean-Square Deviation
3-6 Test Interval This Work Box-Muller von Neumann
( )1 2
µ± σ 6.09 10× −1 6.09 10× −1 6.09 10× −1
µ σ± 1.58 10× −1 1.59 10× −1 1.59 10× −1
2
µ± σ 2
1.30 10× − 2
1.35 10× − 2
1.35 10× − 3
µ± σ 4.20 10× −3 4.08 10× −3 4.15 10× −3
4
µ± σ 3
4.20 10× − 3
3.56 10× − 3
3.53 10× − 5
µ± σ 3.26 10× −3 3.13 10× −3 3.11 10× −3
As a measure of efficiency, we compared the central processing unit (CPU) times of the computer during the execution of the program using each algorithm. The results consistently showed that our algorithm is slower than the Box-Muller method by about a factor of two, but faster that the von Neumann rejection me-thod by about a factor of four.
5. Summary and Conclusions
Since random numbers are extensively used in various fields, such as computa-tional physics and other science, we have reviewed them in this work. But spe-cifically we have focused on machine generated pseudo-random numbers that are in most cases uniformly distributed over the interval
[ )
0,1 .However, in many situations non-uniform random numbers, often with nor-mal or Gaussian distribution, are needed. These random numbers are generated by two common methods, namely, the Box-Muller and the von Neumann rejec-tion methods, which we have briefly reviewed in this article.
We have then suggested a third, yet very simple and efficient, algorithm for generating random numbers with a specified normal or Gaussian distribution. The suggested algorithm relies on a modified central limit theorem, and uses the average of uniformly distributed random numbers in the interval
[ )
0,1 . The algorithm generates random numbers with the required normal probability distribution function very accurately using a small number of uniform random numbers in the averaging process.In comparison with other methods, the suggested algorithm is as accurate as the Box-Muller and the von Neumann rejection algorithms. In terms of the effi-ciency or the speed with which the random numbers are generated, however, our algorithm is slower than the Box-Muller method by about a factor of two, but faster than the von Neumann rejection method by about a factor of four.
Considering the accuracy, simplicity, and the efficiency of the suggested algo-rithm, it can justifiably compete with the existing methods.
DOI: 10.4236/jamp.2019.711185 2721 Journal of Applied Mathematics and Physics
Acknowledgements
This work was supported by a URAP grant from the University of Wisconsin- Parkside.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this pa-per.
References
[1] Gould, H. and Tobochnik, J. (1996) An Introduction to Computer Simulation Me-thods. 2nd Edition, Addison-Wesley, New York, 358-361.
[2] Landau, R.H. and Páez, M.J. (1997) Computational Physics. John Wiley and Sons, New York, 104-105.
[3] Gould, H. andTobochnik, J. (1996) An Introduction to Computer Simulation Me-thods. 2nd Edition, Addison-Wesley, New York, 371-372.
[4] Giordano, N.J. (1997) Computational Physics. Prentice Hall, Upper Saddle River, NJ, 161-163.
[5] Allen, M.P. and Tildesley, D.J. (1987) Computer Simulation of Liquids. Clarendon Press, Oxford, Great Britain, 349-351.
[6] Grinstead, C.M. and Snell, J.L. (1997) Introduction to Probability. 2nd Revised Edi-tion, American Mathematical Society,Providence, RI, 269-270.
[7] Wikipedia (2019) Variance. https://en.wikipedia.org/wiki/Variance [8] Pitman, J. (1993) Probability. Springer-Verlag, New York, 196.
https://doi.org/10.1007/978-1-4612-4374-8
[9] Wani, J.K. (1971) Probability and Statistical Inference. Appleton Century Crofts, Meredith Corporation, New York, 154-156.
[10] Wallace, P.R. (1984) Mathematical Analysis of Physical Problems. Dover Publica-tions, Inc., New York, 431.
[11] Burington, R.S. and May Jr., D.C. (1970) Handbook of Probability and Statistics with Tables. 2nd Edition, McGraw-Hill, New York, 190.
[12] Witte, R.S. and Witte, J.S. (2007) Statistics. 8th Edition, John Wiley & Sons, Hobo-ken, NJ, 199-204.
[13] Wikipedia (2019) Dirac Delta Function.
https://en.wikipedia.org/wiki/Dirac_delta_function
[14] Byron Jr., F.W. and Fuller, R.W. (1970) Mathematics of Classical and Quantum Physics. Dover Publications, New York, 447-448.
[15] Liboff, R.L. (2003) Introductory Quantum Mechanics. 4th Edition, Addison Wesley, New York, 74-75.
[16] Press, W.H., Flannery, B.P., Teukolsky, S.A. and Vetterling, W.T. (1986) Numerical Recipes. Cambridge University Press, New York.
[17] Haile, J.M. (1997) Molecular Dynamics Simulation. John Wiley & Sons, New York, 376-377.
DOI: 10.4236/jamp.2019.711185 2722 Journal of Applied Mathematics and Physics [19] Landau, R.H. and Páez, M.J. (1997) Computational Physics. John Wiley and Sons,
New York, 84-86.