D Apriori: An Algorithm to Incorporate Dynamism in Apriori Algorithm
Full text
Figure
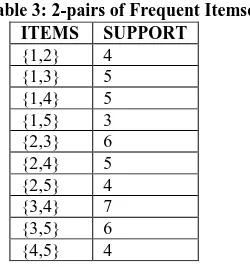
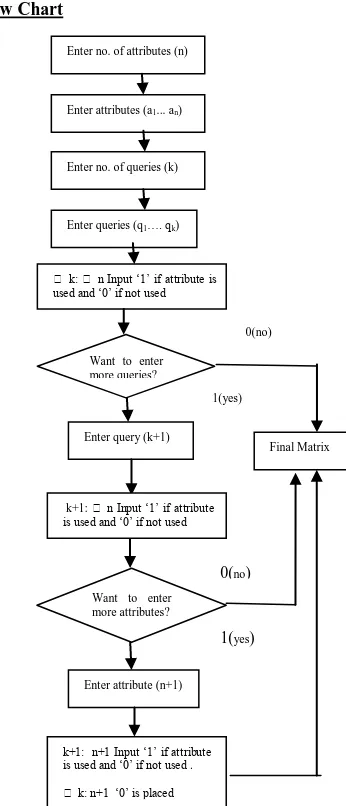


Related documents
In this section we introduce primitive recursive set theory with infinity (PRSω), which will be the default base theory for the rest of this thesis (occasionally exten- ded by
This paper proposes a tolerant control for the open- circuit fault of the outer switches in three-level rectifiers (both 3L-NPC and T-type topologies) used in
Canada’s superannuation system, known as the retirement income system, comprises a publicly managed pension scheme, privately managed retirement savings schemes, and
Body composition indices (psoas muscle index (PMI); psoas muscle attenuation (PMA); subcutaneous adipose tissue index (SATI); visceral adipose tissue index
We also prove in Appendix A that (a) our attack results in a transcript that can convince skeptical, offline veri- fiers [Theorem 1], (b) that any authenticated messaging protocol
Conclusion: Significant and sustained reduction in IOP and medications with a favorable safety profile was shown through 3 years after implantation of 2
A waiver can be limited to (1) a specific tribal asset or enterprise revenue stream, (2) a specific type of legal relief sought by performance of the contract and not money
Across Kratie and Stung Treng, Bolikhamsay, and Xayabouly, between 55-70% of farmers report damage from the disease while the rate of damage reported is on par or even higher for