Balanced Decomposition of Hypercube

2017 2nd _{International Conference on Artificial Intelligence and Engineering Applications (AIEA 2017)} ISBN: 978-1-60595-485-1

Balanced Decomposition of Hypercube

RUI LI

ABSTRACT

A balanced vertex coloring of Gis a pair



R,B



of subsetsR,BV

 

G such that

  B

R and R  B . A subset U of V

 

G is called a balanced set if Uinduces a connected subgraph with UR UB. A balanced decomposition of a balanced coloring



R,B



of G is a partition of vertices V

 

G V1V2Vr such that all

parts V_i,s are balanced sets. The size of the balanced decomposition is defined as the maximum of V1,,Vr . The balanced decomposition number of a graph is the

maximum size of the balanced decompositions withR  B k, where 0k

 

n 2 .

In this paper, some results about balanced decomposition of n-dimensional cube Q_n

are given.

KEYWORDS

Balanced decomposition, vertex partition

INTRODUCTION

Let Gbe an undirected graph with no multiple edge or loop. Let V

 

G and E

 

G be the vertex set and edge set of G.A balanced vertex coloring of Gis a pair



R,B



of subsetsR,BV

 

G such that RBand R  B . We also say that a balanced vertex coloring



R,B



has order kif R  B k. The sets



R,B



are regarded as a red set and a blue set. If a vertex v is in RB, vis called colored, and otherwise, vis called uncolored.

Let



R,B



be a balanced vertex coloring ofG . Let U G. LetG

 

U be the subgraph ofGinduced by U. If G

 

U is connected and UR UB, then U is called a balanced set. A balanced decomposition of a balanced coloring



R,B



of Gis a partition of vertices V

 

G V1V2Vr

such that all parts V_i,s are balanced sets. The size of the balanced decomposition is defined as the maximum of V1,,Vr .

_________________________________________

We refer the reader to [1] for any undefined terms. In [2], Fujita and Nakamigawa introduced the balanced decomposition number of a graph. Now, observe that, if Gis a disconnected graph, then we can take a balanced coloring so thatGdoes not have a balanced decomposition at all. Simply, color one vertex in one component red, and another vertex in another component blue. So, from now on, we shall only consider balanced decompositions for connected graphs.

So, ifGis a connected graph onnvertices, and kZ , 0k 

 

n 2 , we define



k G





f , min{sN: Every balanced colouring



R,B



of G with

k B

R   has a balanced decomposition of size at most s}.

Note that f



k,G



n, so f



k,G



is well-defined. The balanced decomposition number of Gis then defined as

 

G max



f



k,G



:0 k

 

n 2



f    .

It is obviously to see that the balanced decomposition number is relevant to the diameter of the graph.

Theorem 1.1 [2] Let G be a connected graph with order at least 2. Let

 

G diam

d  . Then

 

1,G d1

f . In particular, f

 

G d1.

The n-dimensional cube or hypercube Q_n is the simple graph whose vertices are

n-tuples with entries in

 

0,1 and whose edges are the pairs of n-tuples that different in exactly one position. In this paper, we will consider some balanced decomposition of Qn.

BALANCED DECOMPOSITION n_{-DIMENSIONAL HYPERCUBE} Q_n

Denote by d

 

u,v the distance between u, in v G.

Theorem 2.1 Let Qn be an n-dimensional cube. Then f



2,Qn



n.

Proof. We first show that f



2,Qn



n . Denote by



0,0, ,0



1 

u andu₂ 



1,0,,0



, u₃ 



1,1,,1



, u₄ 



0,1,,1



. Let us consider a balanced vertex coloring



R,B



of Qn with R



u1,u2



and B



u3,u4



. Let



0,0,0, ,0



0,1,0, ,0



0,1,1, ,0

 

0,1,1, ,1



1      

P be a shortest path connecting u₁

with u₄, and P₂ 



1,0,0,,0



1,1,0,,0



1,1,1,,0

 

1,1,1,,1



be a shortest path between u₂ and u₃. It is easy to see that the lengths of both P₁ and P₂ are no more than n1 . Thus we obtain a balanced decomposition V

 

Q_n V

 

P V

 

P



_{u V   P V P}



 

u

2 1

2

1    

  . Since



u1,u3



n d



u1,u4



d   , and P₁is a shortest path, the size of the above decomposition is smallest, f



2,Q_n



V

 

P_i n, i1,2.

Next, we will show that f



2,Qn



n. Let



R,B



be a balanced decomposition of

n

Q with R  B 2, and R



u₁,u₂



, B



u₃,u₄



. Note that there is only one

Assume that the i-th coordinate is the first different coordinate between u₃ and

4

u . Without loss of generality, the i-th coordinate of u₃ is 0, u₄ is 1. Then we can get a shortest u₁u₃-path or u₂u₃-path P₁ and all of the internal vertices in P₁ have the same i-th coordinate 0. Similarly, we also can obtain a shortest path P₂ between u₂ and u₄ or between u₁ and u₄, and all the i-th coordinate in the internal vertices of P₂ are 1. Thus P₁ and P₂ are two internal disjoint paths.

If the vertices with distance n to u₁,u₂ are not in B, then the length of P_i is no

more than n1 for i1,2 . And the size of the balanced decomposition

   

Q V P V

 

P



   



 

u

V _{n u V P V P}

2 1

2

1    

  is at most n . If d



u₁,u₃



n and



u u



n

d ₂, ₄  , then we can find a shortest u₂u₃-path P₁ and a shortest

4 1u

u -path P₂, and P₁ is internal disjoint with P₂. Obviously, the length of P_i is no

more than n1. It follows that there is a balanced decomposition of G as above with size no more than n.

Similarly, we can consider the cases d



u₁,u₃



n and d



u₂,u₄



n , or



u u



n

d ₁, ₃  and d



u₂,u₄



n .■

Theorem 2.2 Let Qn be an n-dimensional cube. Then f



3,Qn



n1.

Proof. Let



R,B



be a balanced vertex coloring of Q_n with R  B 3. Without loss of generality, let R



u₁,u₂,u₃



and B



v₁,v₂,v₃



. Note that Qncan

be constructed by two subgraph isomorphism to Qn_1which connect with a perfect

matching. So, V(Qn) can be partitioned into two parts according to some coordinate, and both of the parts induce a Q_n1, written Q0n1 and Q1n1, and



RB



Q_n1  for i0,1. Denote by M the perfect matching connecting Q0n1 and Q1n1.

By symmetry, we consider the following cases. Case 1. RQ0n1 u₁, BQ0n1.

Argument as above Theorem 2.1, we can obtain two internal disjoint shortest

j iv

u -paths P₁,P₂ in Q1n1, and the length of P₁,P₂is no more thann2, where 3

, 2



i , j1,2,3. Suppose that v₁,v₂ is one of the end vertex of P₁,P₂ respectively. If

 

Pi

V

v₃ , then let v₃ be the end vertex of Pi. Otherwise, suppose that vv3M '

3 . Then v₃'Q0n1. Choose that P₃' be a shortest u₁v₃' -path in Q0n1. Obviously, the length of '

3

P is no more than n1. Setting P₃ P₃'v₃v₃', then the length of P₃ is at

most n . Thus we have V

 

Q V

 

P



_{ }



 

u

i i V P u i i

n 3

1

3

1  _

 

  _ , it is a balanced decomposition with size at most n1.

Case 2. RQ0n1 {u₁,u₂}, BQ0n1 .

By the Theorem 2.1, we have two internal disjoint path ' 2 ' 1,P

P from u₁,u₂ to v₁',v₂'

with length at most n2. Choose that P₁P₁'v₁v₁',P₂ P₂'v₂v₂'. Then we get a

balanced decomposition with size at most n, V

 

Q V

 

P



_{ }



 

u

i i V P u i i n 3 1 3

1  _

 

  _ .

Case 3. RQ0n1, BQ1n1.

Let u_i'u_i,v_i'v_iM , i1,2,3. Denote by P₁' a shortest path from u₁',u₂',u₃' to B. If

some uiB

' _{, then the length of} ' 1

P is zero. Suppose that u₁',v₁ are the end vertices of

' 1

P. Let P₂' be a shortest path from u₂',u₃' to Bv₁. Similarly, we suppose that u₂',v₂

are the end vertices of ' 2

P. According to the argument as above, P₁',P₂' may internal

disjoint, and ' 2 ' 1 3 P P

v   , both the lengths are at most n2. Let '

3

P be a shortest u₃',v₃-path in Q0n1. Then the length of P₃' is no more than 1



n . Denote Pi Pi'uiui', i1,2,

' 3 3 ' 3 3 P vv

P   . Obviously, the lengths of the

three paths are at most n . Then the balanced decomposition

 

Q V

 

P



_{ }



 

u

V

i i V P u i i n 3 1 3

1  _

 

  _ is as required. Case 4. RQ0n1 u₁, BQ0n1v₁.

Similarly, we can find path P₁ with length at most n1 in Q0n1, and two disjoint paths P₂,P₃ in Q1n1 with lengths at most n2 . Then

 

Q V

 

P



_{ }



 

u

V

i i V P u i i n 3 1 3

1 _{ }

 

  _ is a balanced decomposition as required. We can deal with the following case as above.

Case 5. RQ0n1 {u₁,u₂}, BQ0n1 v₁.

Overall, there is a balanced decomposition with size at most n1. This completes the proof. ■

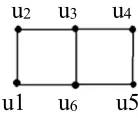
Theorem 2.3 f

 

Q₃ 4.

Proof. From the Theorems 1.1, 2.1 and 2.2, we only need to show that



4,Q₃



4

f . Let



R,B



be a balanced decomposition of Q₃ with R  B 4. Let

R

u . If vN

 

u and vB, then Q₃uv is isomorphism to the follow graph 1.

It is easy to see that the graph has an edge not u₃u₆ colored different. Assume that it is

2 1u

u . Delete u₁u₂ , then the graph 1 changes to a path with length 3 . Thus,

 

Q3 uv u1u2 u3u4u5u6

V    is a balanced decomposition of Q₃ with size no more

than 4 . Hence f

 

Q₃ 4.

u2 u3 u4

[image:4.612.282.351.592.651.2]

u1 u6 u5

ACKNOWLEDGEMENTS

The author is partially supported by NSFJP (No. BK20170862) and NSFC 11701142, 11426085.

REFERENCES

1. B. Bollobás, Modern graph theory, Springer-Verlag, New York, 1998, p. xiii+394.